La justificació d'aquesta pregunta va ser, amb el tema dels vectors, que els seus números ens determinen la posició respecte un eix de coordenades, és a dir:

Aquestes dades corresponen a les coordenades respecte a la base canònica en el pla. És a dir, el pla té dos eixos que els nombres dels vectors ens diuen on comença i on acaba el vector. Seguint aquesta lògica en la tercera dimensió seria així,

és a dir, per cada eix, un número. La pregunta, com ja es preveu, és: en la quarta dimensió els possibles vectors tenen quatre nombres i, per tant, en la quarta dimensió hi hauria quatre eixos?

Com ja es veu, el tema central de la nostra recerca requeia en descobrir com dibuixar o representar figures comunes per nosaltres, com ara la circumferència, el quadrat, el cub... en la quarta dimensió. També preteníem arribar a percebre la quarta dimensió en si, és a dir, poder-la veure realment, i no pas a apreciar exclusivament una representació tridimensional de la quarta dimensió. Totes les figures que aconseguirem són representacions de la quarta dimensió en tres dimensions. També, en un principi, ens preguntàrem si podríem fer un programa per a ordinador per fer les representacions de figures de la quarta dimensió. Però, un cop estudiat, ens adonàrem que, a mesura que es puja de dimensió en dimensió es guanya informació gràfica, però, si es retrocedeix, se'n perd. Per tant, en una pantalla que és bidimensional, es perdria tanta informació que el resultat esperat no es veuria, i tampoc tindria l'espectacularitat desitjada. A mesura que es va avançant en dimensió les figures van esdevenint més perfectes i complexes. Aquesta perfecció consisteix en perdre cada cop més la semblança en la figura original amb la dimensió que apareix. Per tant, vàrem desistir de realitzar aquest projecte.

En un principi estàvem molt confosos de quin significat podia tenir la variable "temps". Nosaltres ja sabíem, per cultureta popular que aquest nou eix que apareixia era el temps. Tampoc sabíem on havia d'anar aquest eix. Per intentar esbrinar on era aquest eix, vàrem buscar informació però, la recerca va ser infructuosa. No vàrem obtenir els resultats esperats. Això ens produí una gran decepció i ens preguntàrem si realment existia la quarta dimensió. La resposta fou immediata: sí que existia com a idea, és a dir cadascú té la seva concepció personal sobre la quarta dimensió, i a l'hora de projectar-la, qui té més informació pot definir, en tres dimensions, amb més precisió que nosaltres. És a dir, qui més coneixements té sobre la quarta dimensió, amb més facilitat pot descriure la idea de la quarta dimensió. Es podria establir el símil dels nombres complexos. Els nombres complexos són una idea perquè com s'entén que un número elevat al quadrat doni negatiu? Quin és el valor de 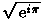? Cal una imaginació suprema per imaginar-se una nova branca als nombres reals. És com si forméssin part d'una altra dimensió de nombres. Per tant aquesta quarta dimensió seria una altra dins la família de dimensions.

La nostra hipòtesi, que intenterem seguir durant tot el treball, és:

La justificació d'aquesta hipòtesi seria la següent: les dimensions gràfiques formen part de la geometria, i aquesta dins de les matemàtiques. Les matemàtiques es comporten amb una certa lògica. Per tant, com que les dimensions formen part de les matemàtiques, aquestes han de tenir una lògica. De la mateixa manera que els vèrtex del la sèrie de la família del quadrat es van duplicant en nombre a mesura que avancem en les dimensions, igual que existeix la trigonometria per a trobar els angles d'un triangle rectangle i que per a tots els triangles en general tenim els teoremes del sinus i del cosinus per al mateix objectiu. Per tant, veiem que dins de les matemàtiques podem establir relacions que ens permeten treballar sense haver tingut experiència prèvia, com per exemple, seria la utilització de l'infinit per trobar la derivada d'una funció, per què, com definim l'infinit? Com l'utilitzem?. Per tant, hi ha d'haver alguna mena de successió que ens permeti establir una relació partint des d'un sol punt, i no des d'una figura de dos dimensions, com una mena de fórmula general que ens permetés calcular i, així, tenir una idea de les diverses figures que podem obtenir durant el nostre viatge al llarg de les dimensions.

Però no avancem esdeveniments.