Pràctica 2. Polinomis i Fraccions algèbriques
Amb la calculadora WIRIS també poden treballar amb expressions algèbriques d’una o més variables i fer operacions: suma, resta, multiplicació, divisió i potències d’aquestes expressions.
1. Anem a veure com es pot fer tot això amb la calculadora WIRIS.
Accediu a la calculadora WIRIS. Cliqueu sobre la pestanya Operacions. Observeu que hi ha unes icones especials per introduir fraccions i exponents.
Introduïu l’expressió x 2 + 5x - 7. Cliqueu Intro. Escriviu a sota l’expressió 3 x2 - 1 . Cliqueu Intro.
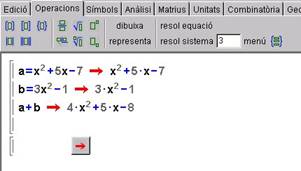Podem anomenar cadascuna d’aquestes expressions amb una lletra o paraula, per exemple: a = x 2 + 5x - 7 i b = 3x2 - 1.
Modifiqueu les dues expressions anteriors perquè quedin de la forma següent:
a = x2 + 5x - 7
b = 3x2 - 1
A la línia de sota escriviu l’expressió: a+b.
Cliqueu Intro. Cliqueu sobre la fletxa vermella que us donarà el resultat.
a. Calculeu la resta i la multiplicació de les dues expressions anteriors i el cub de la segona:
(x2 + 5x -7) – (3x2 - 1) =
(x2 + 5x - 7) · (3x2 - 1) =
(3x2 - 1)3 =
b. Calculeu el resultat de les operacions següents:
(5x3 + 6y2 - 7)·(4x - 3z) =
(a + b)7 =
Observeu que
2. Accediu a la calculadora WIRIS i definiu els polinomis següents:
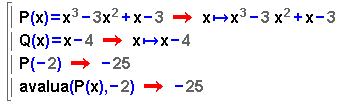P(x) = x3 – 3x2 + x – 3
Q(x) = x – 4
Per calcular el valor numèric del polinomi P(x) per x = -2 podem escriure:
P(-2)
o també:
avalua(P(x),-2)
a. Quin és valor numèric del polinomi Q(x) per x = –2 ? I del polinomi P(x) per x = 17 ?
Per factoritzar el polinomi P(x) només cal escriure: factoritza(P(x))
Un cop factoritzat el polinomi, podem conèixer les seves arrels. De tota manera,
També, un cop factoritzat, podem resoldre l’equació P(x) = 0; doncs les arrels d’aquest polinomi són les solucions d’aquesta equació. Així, obtindrem el mateix resultat que fent:
resol(P(x)==0)
b. Factoritzeu el polinomi P(x) = x3 – 3x2 + x – 3. Quines són les arrels d’aquest polinomi ? Resoleu l’equació x3 – 3x2 + x – 3 = 0.
La calculadora WIRIS ens permet trobar el quocient i el residu de la divisió de dos polinomis (també, de la divisió de dos nombres).
Cliqueu sobre la pestanya Operacions. Cliqueu sobre la icona 
i ompliu els forats amb P(x) i Q(x) per fer la divisió de P(x) entre Q(x).
c. Quin és el quocient ? I el residu ?
d. Calculeu el quocient i el residu de la divisió de –2x4 + 5x3 –7x + 21 entre x2 + 7x - 2.
Per simplificar fraccions algèbriques i fer operacions només cal introduir les fraccions i clicar sobre la icona 
.
e. Introduïu la fracció algèbrica: 
cliqueu sobre la icona .
Introduïu la suma de fraccions algèbriques: 
cliqueu sobre la icona .
Introduïu el producte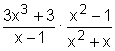 
cliqueu sobre la icona .
Quins resultats heu obtingut ?
Guarda el treball per fer-ho cal tornar a edició i seleccionar 
Prepara la sessió per a guardar-la en un arxiu HTML. anomena’l polinomis1 i deixeu-lo en el vostre disquet dins una carpeta anomenada polinomis.
3. Polinomis i Fraccions algèbriques
Ø Accediu a l’adreça : http://www.xtec.net/aulanet/ud/mates/polinomis/index.htm
Ø Aneu a l’apartat d’activitats i seleccioneu exercicis de reforç.
Caldrà fer els següents exercicis amb l’ajut de llapis i paper.
Exercici 1
Aneu a l’apartat operacions amb polinomis i feu l’exercici 5.
Cal guardar la resposta fent una impressió de pantalla en un document Word que guardareu en el vostre disquet dins una carpeta anomenada polinomis. Anomena’l polinomis2.
Exercici 2
Aneu a l’apartat exercicis de reforç / identitats notables i feu els exercicis 1 i 2 .
Cal guardar la resposta amb l’opció : Edició i guardaren la carpeta anterior com un arxiu htlm. Anomena’l polinomis3
Exercici 3
Aneu a l’apartat exercicis de reforç / arrels i equacions i feu els exercicis 2,3 i 5.
Cal guardar la resposta fent una impressió de pantalla en el document Word .
Exercici 4
Aneu a l’apartat exercicis de reforç / factorització i feu l’exercici 1.
Cal guardar la resposta fent una impressió de pantalla en el document Word.