| Teoremes
Fonamentals de l'electrònica |
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
| Unitat
0.0. Introducció. |
|
|
Electró.
Gira al voltant del nucli gràcies a la força d’atracció que
aquest exerceix sobre ell. La seva càrrega elèctrica és negativa
i té una massa de 9,1091 · 10 –31 kg.
Protó.
Es troba al nucli dels àtoms i té una càrrega elèctrica idèntica
als electrons però de signe contrari. (carrega positiva).
La seva massa és molt superior a la d’electró, gairebé 2000
vegades. (1836,11)
Neutró.
També es troba al nucli i té una massa similar al protó però,
no té càrrega elèctrica.
Els
àtoms en equilibri tenen el mateix número d’electrons
que de protons restant elèctricament neutres.
Quan un àtom perd un electró, es converteix
en un IÓ POSITIU, ja que el nombre de protons
és superior al d’electrons, i tindrà una càrrega positiva.
Quan la capa de valència guanya un electró,
parlarem d’un IÓ NEGATIU, i direm que és
elèctricament negatiu. |
Els
Àtoms. Tot
fenòmen elèctric té com a base l’estructura atòmica
dels 107 elements o cossos simples que es poden trobar a la
natura. Un àtom es pot dividir en dues parts: el nucli ( neutrons
i protons) i l’escorça ( electrons). És cert que podem
trobar més partícules subatòmiques com ara: els positrons,
els neutrins, els mesons, els antiprotons...però per ara només
ens interessen el nucli i els electrons. |
|
Càrrega
elèctrica.Tot
cos està elèctricament càrregat, la seva càrrega només dependrà
del nombre d’electrons que té. Com
què l’electró té una càrrega elèctrica molt petita es fa servir
el Coulomb (C), (sistema internacional) 1C = 6,24 · 10 18
electrons. |
|
|
Energia
potencial elèctrica. Serà
el treball necessari per transportar una càrrega elèctrica
dins un camp magnètic. |
|
|
Potencial
elèctric. El
potencial elèctric ( en volts) (V) d’un punt, és directament
proporcional a l’energia potencial elèctrica ( en joules )
(J) d’aquest punt, i inversament proporcional a la Càrrega
elèctrica del mateix. |
|
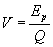 |
|
|
Diferència
de potencial. La
diferència de potencial entre dos punts és, el treball que
cal fer per traslladar una càrrega des d’un punt a l’altre. |
|
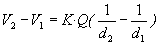 |
|
|
Conductor.
Entendrem com a conductor, tot material
que permeti el pas del corrent elèctric a traves seu. Els
millors conductors són els metalls. En ells, l’enllaç electrònic
és metàl·lic, el que fa que alguns electrons queden lliures,
facilitant així el pas de nous electrons a traves seu.
Aïllant,
dielèctric o no conductor. Serà
tot material que no permeti el pas del corrent elèctric a
traves seu. Quan per un material dielèctric passi corrent,
direm que el material ha perdut les seves propietats dielèctriques.
Semiconductors.
Alguns
materials com ara el silici, el germani, el seleni, s’uneixen
entre ells mitjançant enllaços covalents, ( Els àtoms comparteixen
electrons de l’ultima capa, la de valència, per tenir una
estructura més estable, però és fàcil que quedin electrons
lliures, el que facilita el pas del corrent en determinades
circumstancies). |
|
|
Circuit
elèctric. |
|
|
|
|
|
Intensitat
del corrent elèctric. Entenem
per intensitat del corrent elèctric el pas d’electrons a través
d’un cos conductor. Convencionalment el sentit d’aquest
corrent és des del pol positiu al negatiu d’un circuit, però
recordem que el corrent és un moviment electrònic ( electró
= càrrega negativa) així que en la realitat ho fa en sentit
contrari.
La
intensitat del corrent elèctric és la quantitat d’electrons
que passa per la secció transversal d’un medi conductor en
la unitat de temps. |
|
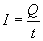 |
|
|
Un
corrent serà continu i constant, quan el flux
d’electrons sigui sempre el mateix i circuli en un sol sentit.
Un
corrent serà continu i variable, quan el flux
d’electrons sigui variable però sempre amb el mateix sentit
de circulació.
Un
corrent serà altern quan el flux i el sentit
de circulació siguin alterns. Els més emprats són el tipus
sinusoïdal i el polsatori. |
|
|
Tot
generador doncs, cedirà a un circuit elèctric una Força
Electromotriu (f.e.m.) en volts (V).
Generarem
electricitat a partir de: la Inducció Electromagnètica
( alternadors i dinamos principalment, tot conductor en moviment
dins un camp magnètic crea una f.e.m.), Reaccions Químiques
( a les piles i bateries es crea una diferència de potencial
entre l’electròlit i les plaques submergides en ell), Reaccions
Fotovoltaiques ( la radiació lluminosa quan incideix
en alguns materials com el silici, liti, seleni,..., fa que
aparegui una petita d.d.p. entre punts del material, aquest
és el principi de les cèl·lules fotovoltaiques), Efectes
piezoelèctrics ( quan deformem mecànicament ( pressió
) el cristall de quars o la turmalina a les seves cares apareix
una d.d.p.), Reaccions Termoelèctriques ( un
termopar és la unió de dos fils conductors - el coure i el
constatà per exemple - en un dels seus extrems, si escalfem
aquesta unió, a l’altre extrem apareix una d.d.p. entre els
dos conductors).
Aquesta
força electromotriu (f.e.m.) no és res més que
el treball desenvolupat pel generador sobre la unitat de càrrega
que circula a traves seu. |
Generadors.
Direm
generador als dispositius que mitjançant l’acció
d’una font d’energia primària obtinguin energia elèctrica
mantenint sempre una diferència de potencial als seus borns
el més constant possible. |
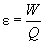 |
|
|
Aquesta
f.e.m. no podrem mesurar-la directament, però si la
Diferència de Potencial (d.d.p.) (V) entre els seus
borns. |
|
|
Per
a què aquests funcionin, han d’ésser travessats per la intensitat
del corrent elèctric, però no tots en faciliten aquest pas.
Entendrem com a Resistència elèctrica, l’oposició
dels cossos a ésser travessats pel corrent elèctric,
i es mesurarà en ohms ( W ). Aquesta
oposició dependrà principalment de naturalesa del cos ( resistivitat
) ( r ) en (W·m),
de la seva longitud ( l ) en (m) i de la secció travessada
( s ) en (m2). |
Receptors.
Direm
Receptors als dispositius capaços de transformar
l’energia elèctrica en energia útil. Tot aparell connectat
elèctricament a una pila, endoll,.., es pot considerar un
receptor. |
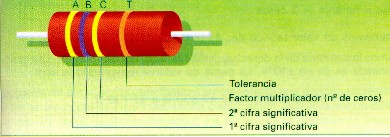
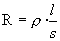 |
|
|
|
|
 |
|
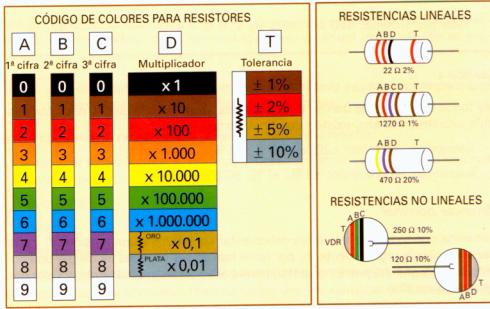 |
|
| Unitat
0.1. Tensió, Resistència i Intensitat. Llei d’Ohm. |
|
|
La
relació entre aquestes tres magnituds l’estableix la llei
d’Ohm. Aquesta ens diu: Que el voltatge o la
diferència de potencial entre dos punts d’un circuit és directament
proporcional a la resistència elèctrica existent entre aquests
punts i al corrent elèctric que els travessa. |
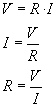 |
|
|
|
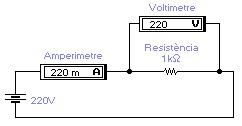
L’aparell
que mesurarà la tensió o la diferència de potencial
entre dos punts és el voltímetre. Aquest el
connectarem en paral·lel als punts que vulguem mesurar. |
 |
|
L’aparell
que mesurarà la intensitat del corrent elèctric
que travessa un receptor o la que dona un generador és l’amperímetre.
Aquest el connectarem en sèrie amb el circuit ja que el corrent
que volem mesurar l’ha de travessar. |
 |
|
L’aparell
que mesurarà directament la resistència d’un
circuit o d’un receptor ( en aquest cas un resistor) és l’ohmetre.
Aquest aparell porta generalment una pila per realitzar les
mesures, així que quan realitzem una mesura haurem de desconnectar
el generador del circuit per no danyar l’aparell de mesura.
Generalment
la resistència es calcula indirectament, ja que si sabem la
intensitat del corrent elèctric i el voltatge en borns d’un
circuit o en els d’una resistència podrem saber-ne aquesta
gràcies a la llei d’Ohm. |
 |
| Unitat
0.2. Llei de Joule. Potència Elèctrica. |
|
|
Entendrem
com a Potència Elèctrica l’energia consumida o produïda
per unitat de temps. |
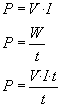 |
|
|
|
Segons
la Llei de Joule, en tot circuit travessat
per un corrent elèctric es produeixen pèrdues de potència
degudes a l’escalfor provocada pel pas d’electrons per un
conductor, receptor,...
Aquestes
pèrdues les denominarem Pèrdues de Potència per efecte
Joule. |
|
|
|
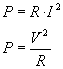 |
 |
L’aparell
que mesurarà directament la potència d’un circuit
o d’un receptor ( en aquest cas un resistor) és el wattímetre.
|
|
|
|
| Unitat
0.3. Associació de Resistències en Sèrie. |
|
|
|
Entendrem
que dos o més resistències estan associades en sèrie
quan la sortida de la primera resistència s’uneixi a l’entrada
de la segona i així successivament, restant una resistència
equivalent que serà la suma de totes elles, amb borns
d’entrada: l’entrada de la primera i la sortida de la darrera. |
| Unitat
0.4. Associació de Resistències en Paral·lel. |
|
|
|
Entendrem
que dos o més resistències estan associades en paral·lel
quan l’entrada de totes elles estiguin unides entre
si, formant l’entrada de la resistència equivalent, de
la mateixa manera s’uniran totes les sortides en un sol punt.
La resistència equivalent que serà: l’invers de la resistència
total serà igual al sumatori de les inverses de les resistències. |
| Unitat
0.5. Associació Mixta de Resistències. |
|
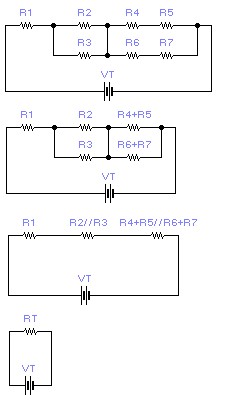 |
L’associació
mixta de resistències és la combinació de les dues associacions
anteriors la sèrie i la paral·lel. Per resoldre aquest
tipus d’exercicis hauràs de simplificar les associacions obtenint
les resistències equivalent i calculant segons cada cas.
|
| |
|
| R6+7
= R 6+ R7 = RS2
|
|
| 1/(Rs1//
Rs2 )= (1/Rs1 )+(1/ R s2)
|
|
| Quan
hi ha dos i només dos resistències |
|
| Rs1//
Rs2 = Rs1 ·R s2 / Rs1
+R s2 =RP1 |
|
| 1/(R2
// R3 )= (1/R2 )+(1/ R 3)
|
|
|
|
|
|
|
|
|
|
|
| Quan
hi h dos i només dos resistències |
|
| (R2
// R3 )= R2 ·R 3 / R2
+R 3 =RP2 |
|
| RT
= RP1 + Rp2 |
VR7=
RR7 · IR7 |
| |
|
|
| |
|
| |
|
| IT=IRP2
= IR2 + IR3 |
|
|
| VRp2=
VR2 = VR3 |
| IR2
= VR2/R2 |
| IR3
= VR3/R3 |
|
| Unitat
0.6. Teoremes de Kirchhoff. |
|
|
El
sentit del corrent en un nus serà el que marqui la fem.
El
sentit convencional del corrent elèctric a les malles serà
el de les agulles del rellotge. Sí un corrent de malla dona
negatiu voldrà dir que el seu sentit és el contrari.
En
una resistència mirarem sempre la influència del corrent de
malla i la influencia del corrent dela malla del costat sí
hi ha. Si el sentit és el mateix se sumarà i si és el contrari
es restarà. |
A
més a més de la llei d’Ohm, podrem fer servir els Teoremes
de Kirchhoff per resoldre exercicis més complexos, on
hi ha moltes incògnites. Cal recordar que per resoldre un
problema amb múltiples incògnites, cal muntar un sistema d’equacions.
Aquí els teoremes de Kirchhoff ens ajudaran. |
 |
|
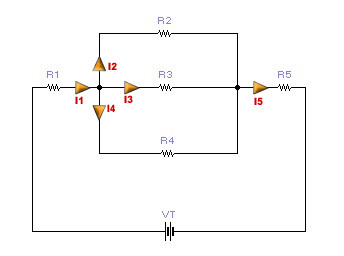
El
sumatori de intensitats de corrent entrants en un nus
és igual al sumatori d’intensitats de corrent sortints.
I1=I2+I3+I4
I2+I3+I4=I5 |
|
1er
Teorema de Kirchhoff. El Teorema dels nusos.
Entendrem
com a nus el punt d’unió físic de varis conductors. |
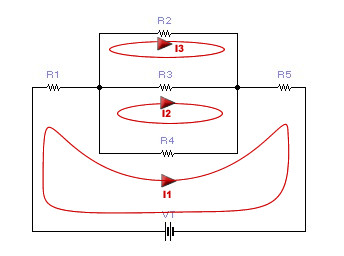 |
| En
una malla – circuit tancat - el sumatori de les forces
electromotrius – generadors, piles- és igual al sumatori
de caigudes de tensió als receptors – productes V=R·I
-. Malla
n º 1. V1=R1·I1+R4·I1+R5·I1-R4·I2
Malla
n º 2. 0V=R3·I2+R4·I2-R4·I1-R3·I3
Malla
n º 3. 0V=R2·I3+R3·I3-R3·I2 |
|
2on
Teorema de Kirchhoff. El Teorema de les malles.
Entendrem
com a malla qualsevol circuit o part d’aquest, en el qual
podem partir d’un punt i tornar a aquest sense passar dues
vegades pel mateix lloc.. |
| Unitat
0.7. Teoremes de Thévenin i Norton. |
|
|
Teorema
de Thévenin |
|
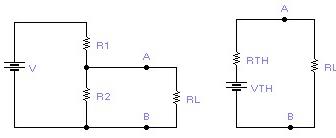 |
Tot
circuit elèctric, amb dos terminals A i B, es pot
substituir per un circuit equivalent format
per una resistència equivalent de Thévenin RTH
en sèrie amb una font equivalent de Thévenin VTH
sense resistència interna. |
|
|
La
tensió equivalent de Thévenin és la diferència de
potencial entre els borns A i B, en circuit obert, es a dir
sense la resistència entre els borns A i B.
|
|
La
resistència de Thévenin es la resistència vista des
de els terminals A i B, quan totes les fonts d’alimentació
han estat curt circuitades.
|
|
Teorema
de Norton. |
|
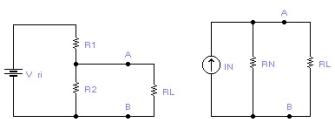 |
Tot
circuit elèctric, amb dos terminals A i B, es pot
substituir per un circuit equivalent format
per una resistència equivalent de Norton RN
en paral·lel amb una font equivalent de Norton VN
sense resistència interna. |
|
|
El
corrent equivalent de Norton és el corrent que circularia
entre els borns A i B, si en la resistència de càrrega es
produís un curt circuit. |
|
La
resistència de Norton es la resistència vista des
de els terminals A i B, quan totes les fonts d’alimentació
han estat curt circuitades o substituïdes per la seva resistència
interrna. |
|
|
Activitats |
|
Activitats
de Teoremes Fonamentals. |
|
|
|
by
Jordi Jordan |