(2024-juny-1-5) Volem construir un petit cobert de fusta de `6` `m^3` de volum, en forma de prisma rectangular, adossat a la paret lateral d’una casa, per a guardar-hi llenya. Només cal construir, per tant, el sostre i tres parets (la paret del fons del cobert és la de la casa a la qual està adossat). A més, volem que el cobert mesuri el triple d’amplària que de fondària. Cada metre quadrat de paret té un cost de construcció de `30 €` i el sostre costa `50 €` per metre quadrat. Un cop construït el cobert, afegir-hi una porta té un cost fix de `35 €`. a) Comproveu que el cost de construcció del cobert ve donat per la funció `C(x)=300/x+ 150x^2 + 35`, on x és la fondària del cobert en metres. [1,25 punts] b) Calculeu quines han de ser les dimensions del cobert per tal que el cost de construcció sigui mínim i justifiqueu la resposta. Quin és aquest cost? [1,25 punts] Solució: 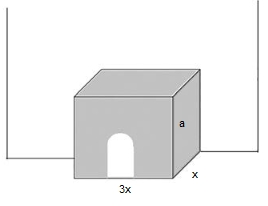a) Per saber l'alçada en funció d'`x` posarem la condició de què el volum val `6` `m^3` `3x·x·a=6=> 3x^2a=6 => a=2/x^2` El cost del sostre `3x·x·50=150x^2` El cost de les pareds: `(2·a·x + a·3x)·30 = a(2x+3x)·30=a·5x·30=(2/x^2·5x)·30=(10/x)·30 =300/x` El cost total, lo anterior més la porta: `C(x)=300/x+150x^2+35` b) Cal trobar el mínim i ho farem derivant la funció: `C'(x)=-300/x^2+300x` `-300/x^2+300x=0` `-1/x^2+x=0` `x=1/x^2` `x^3=1` `x=1` Per comprovar que és un mínim calcularem la segona derivada. `C'(x)=600/x^3+300` `C'(1)=600/1^3+300=900>0` Mínim. I ara només ens queda calcular el cost: `C(x)=300/x+150x^2+35` `C(1)=300/1+150*1^2+35 = 485` `€` I les dimensions: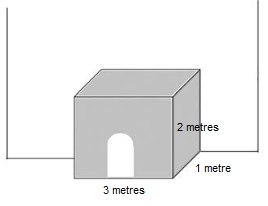