|
Llibre Matemàtiques 2n Batxillerat McGrawHill (Besora, Guiteras, Jané) 1-Calcula els límits següents: 
2-Calcula els límits següents: a- `\lim_{x\to \+infty} ((2x+3)/(2x-1))^x` 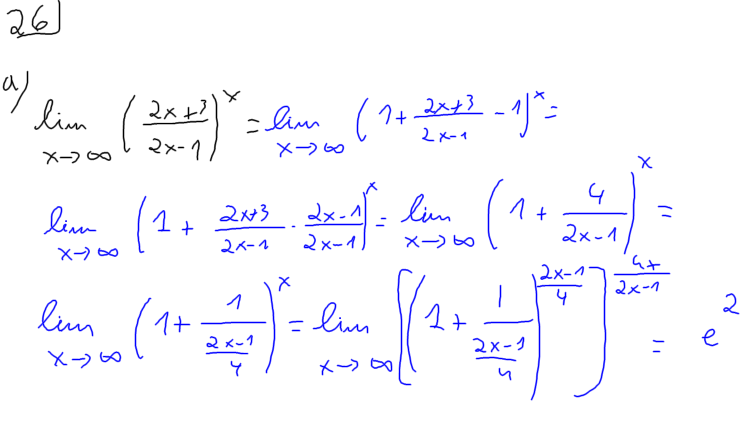
b- `\lim_{x\to 0} (1+x)^(3/x)` SOLUCIÓ:
`\lim_{x\to 0} ln(1+x)^(3/x)` `\lim_{x\to 0} (3ln(1+x))/x=0/0` `\lim_{x\to 0} ((3ln(1+x))')/(x')` `\lim_{x\to 0} (3/(1+x))/1` `\lim_{x\to 0} 3/(1+x)=3` `\lim_{x\to 0} ln(1+x)^(3/x)=3` `e^(\lim_{x\to 0} ln(1+x)^(3/x))=e^3` `\lim_{x\to 0} e^(ln(1+x)^(3/x))=e^3` `\lim_{x\to 0} (1+x)^(3/x)=e^3` c- `\lim_{x\to \infty} (1+1/x)^x` d- `\lim_{x\to \infty} ((x+1)/(x-1))^(3x)` 3-Calcula els límits següents: a- `\lim_{x\to 0} (1-cosx)^(2x)` SOLUCIÓ:
`\lim_{x\to 0} 2xln(1-cosx)` `\lim_{x\to 0} ln(1-cosx)/(1/(2x))=\infty/\infty` `\lim_{x\to 0} ((ln(1-cosx))')/((1/(2x))')` `\lim_{x\to 0} (sinx/(1-cosx))/(-1/(2x^2))` `\lim_{x\to 0} (-2x^2sinx)/(1-cosx)=0/0` `\lim_{x\to 0} ((-2x^2sinx)')/((1-cosx)')` `\lim_{x\to 0} (-4xsinx-2x^2cosx)/sinx=0/0` `\lim_{x\to 0} ((-4xsinx-2x^2cosx)')/((sinx)')` `\lim_{x\to 0} (-4(sinx+xcosx)-2(2xcosx+x^2(-sinx)))/(cosx)` `\lim_{x\to 0} (-4sinx-4xcosx-4xcosx+2x^2sinx)/(cosx)` `\lim_{x\to 0} (-4sinx-8xcosx+2x^2sinx)/(cosx)=0/1=0` `\lim_{x\to 0} ln(1-cosx)^(2x)=0` `e^(\lim_{x\to 0} ln(1-cosx)^(2x))=e^0` `e^(\lim_{x\to 0} ln(1-cosx)^(2x))=e^0` `\lim_{x\to 0} e^(ln(1-cosx)^(2x))=1` `\lim_{x\to 0} (1-cosx)^(2x)=1` b- `\lim_{x\to \pi/2} (sinx)^tanx` c- `\lim_{x\to 0} (e^x-e^(-3x))/ln(1+x)` d- `\lim_{x\to 0} x^4lnx` SOLUCIÓ:
`\lim_{x\to 0} lnx/(1/x^4)=\infty/\infty` `\lim_{x\to 0} ((lnx)')/((1/x^4)')` `\lim_{x\to 0} (1/x)/((-4)/x^5)` `\lim_{x\to 0} (x^5)/(-4x)` `\lim_{x\to 0} (x^4)/(-4)=0` 4-Calcula els límits següents: a- `\lim_{x\to 0} (xcosx-sinx)/x^3` b- `\lim_{x\to 0} (e^x-e^(-x)-2x)/(x-sinx)` c- `\lim_{x\to 0} ((1-cosx)sinx)/x^2` |