|
13-(2020-juny-3-2) S'han trobat unes pintures rupestres en una cova situada en una zona molt pedregosa. Hi ha un camí que voreja parcialment la cova format per l'arc de corba `y = 4 - x^2` d'extrems `(0, 4)` i `(2, 0)`. La cova està situada en el punt de coordenades `(0, 2)`, tal com es mostra en la figura, i es vol habilitar un accés rectilini `d` des del camí a la cova que sigui el més curt possible. 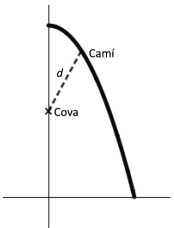 a) Identifiqueu a la gràfica de la figura les coordenades de la cova i del punt del camí des d'on es vol habilitar l'accés. Comproveu que la funció `f(x)=sqrt(x^4-3x^2+4)` calcula la distància des de cada punt del camí a la cova. b) Calculeu les coordenades del punt del camí que queda més a prop de la cova i digueu quina serà la longitud de l'accés `d`. a- Els punts de la corva són `(x,4-x^2)`. La distància al punt on hi ha la cova `(0,2)` és el mòdul del vector que va d'un punt a l'altre. 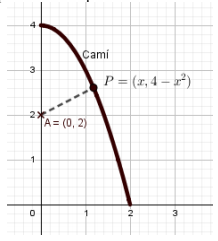 `d(x) =|(x-0,4-x^2-2)|=|(x-0,2-x^2)|=sqrt(x^2+4-4x^2+x^4)=sqrt(x^4-3x^2+4)` b- `d'(x)=(4x^3-6x)/(2sqrt(x^4-3x^2+4))` Per trobar el mínim cerquem on la derivada vol `0`
`x_1=0` `4x^2-6=0 => x_2=sqrt(3/2)`. No agafem la solució negativa ja que el camí està en el 1r quadrant. Cerquem les distàncies de
`d(sqrt(3/2))=sqrt(sqrt(3/2)^4-3sqrt(3/2)^2+4)=sqrt(9/4-9/2+4)=sqrt(9/4-18/4+16/4)=sqrt(7/4)=sqrt(7)/2 \approx 1,32` Que és més petit que `d(0)=2`. Calculem la distància en el punt de tall amb l'eix d'abscises `4-x^2=0 => x=2`
`d(0) > d(sqrt(3/2)) < d(2)=>` a `x=sqrt(3/2)` hi ha un mínim. Falta trobar la coordenada `y=4-(sqrt(3/2))^2= 4-3/2=5/2` En resum, en el punt `(sqrt(3/2), 5/2)` la distància a la cova és mínima i val `sqrt(7)/2` `u` |