15-(2020-juny-3-6) Una empresa de ceràmica vol posar a la venda una rajola quadrada de `20` `cm` de costat pintada a dos colors, de manera que la superfície de cada color sigui la mateixa i que si es posen les rajoles l’una al costat de l’altra es vegi un dibuix continu (figura 1). 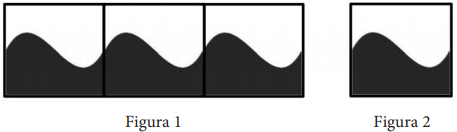Per a fer-ho, l’empresa utilitza en cada rajola la funció `f(x) = x^3 – 3x^2 + 2x + 1` enquadrada entre els punts de coordenades `(0, 0)`, `(0, 2)`, `(2, 0)` i `(2, 2)`, tal com es mostra en la figura 2, i fa servir com a unitat de mesura el decímetre. a) Justifiqueu que, efectivament, aquesta funció permet ajuntar les rajoles de manera contínua i derivable. b) Justifiqueu que aquesta funció divideix el quadrat esmentat en dues parts que tenen la mateixa superfície. a- La funció ha de ser contínua i derivable a `x=2` i ha de coindicir amb la imatge i la derivada en el punt `x=0`. `f(0)=1` i `f(2)=2^3-3·2^2+2·2+1=8-12+4+1 => f(0)=1=f(2) =>` és contínua Calculem la derivada, `f'(x)=3x^2-6x+2` i calculem `f'(0)=2` i `f'(2)=3·2^2-6·2+2=12-12+2 => f'(0)=2=f'(2) =>` és derivable b- Cal calcular la integral definida entre `0` i `2` i veure que és la meitat de l'àrea de cada rajola. Àrea rajola `=2·2=4u^2` `\int_0^2 x^3-3x^2+2x+1 dx= [x^4/4-x^3+x^2+x]_0^2= (2^4/4-2^3+2^2+2)-(0)=4-8+4+2=2u^2` Que és la meitat de l'àrea de la rajola.