16-(2020-setembre-4-1) Siguin les funcions `f(x) = x^3` i `g(x) = ax^2`, en què `a` és un nombre real positiu. a) Trobeu, en funció del paràmetre `a`, els punts de tall entre les dues corbes `y = f(x)` i `y = g(x)` i feu un esbós de la regió limitada per les dues gràfiques. b) Calculeu el valor de `a` perquè l'àrea compresa entre `y = f(x)` i `y = g(x)` sigui `27/4u2`. a- `x^3=ax^2 => x^3-ax^2=0 => x^2(x-a)=0 => x_1=0` i `x_2=a` `f(x_1)=0^3=0 => (0,0)` 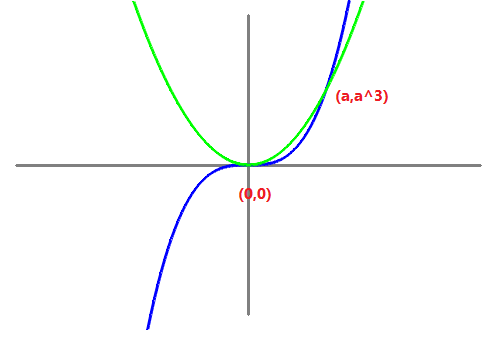`f(x_2)=a^3 => (a,a^3)` b- `\int_0^a (ax^2-x^3)dx=[(ax^3)/3-x^4/4]_0^a=a^4/3-a^4/4=a^4(1/3-1/4)=` `a^4/12=27/4 => a^4=81 => a=3` La solució `a=-3` la descartem, ja que l'enunciat iu que `a>0`