(2022-juny-2-1) Sigui `f '(x) = 3x^2– 12x` la derivada d’una funció `f(x)`. a) Si sabem que `f(x)` talla l’eix de les abscisses en `x = 1`, calculeu l’expressió de la funció `f(x)`. [0,75 punts] b) Calculeu l’abscissa del punt d’inflexió de `f(x)` i estudieu la concavitat de la funció. [0,75 punts] c) Sabem que l’àrea del recinte limitat per la corba `y = f''(x)`, l’eix de les abscisses i les rectes `x = 0` i `x = a`, amb `a > 2`, és `15 u^2`. Calculeu el valor de `a`. [1 punt] SOLUCIÓ: a) Cal trobar la integral indefinida de `f(x)=\int` `(3x^2– 12x)` `dx=x^3-6x^2+C` i saem que passa pel `(1,0)` i això ens permetrà saber `C`. `f(1)=1^3-6·1^2+C=1-6+C=0 => C=5` `f(x)=x^3-6x^2+5` b) Per trobar l'abscissa del punt d'inflexió cal trobar on `f''(x)=0 => f''(x)=6x-12 => 6x-12=0 =>` `x=2` Per trobar on és còncava i on és convexa calcularem el signe d'`f''(x)` a l'esquerra i a la dreta del punt d'inflexió `=>` `f''(0)=-12<0` negatiu (considerem convexa on la segona derivada és negativa) `=> (-\infty, 2)` convexa. `f''(4)=12>0` positiu `=> (2, +\infty)` còncava NOTA: Hi ha llibres i matemàtics que ho consideren al revés ANNEX: (No ho demanen) Dibuixem `f(x)` per veure on hi ha el punt d'inflexió i la concavitat i al convexitat: 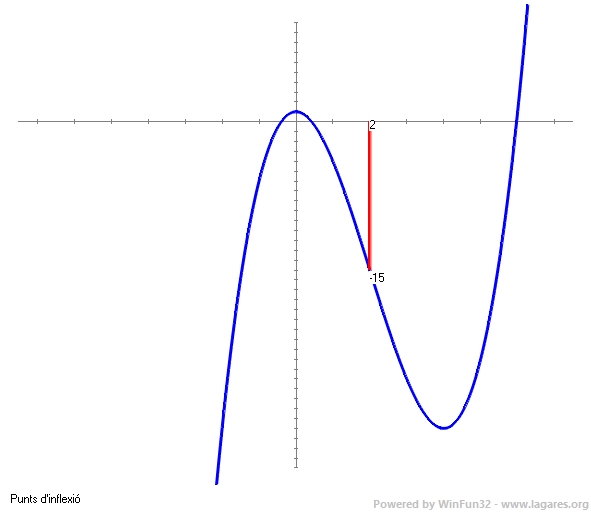c) El que ens demanen és la integral definida entre `[0,a]` de `f''(x)=6x-12`, però com `a>2` i en `x=2`, `f''(x)` té un punt de tall. Caldrà calcular la integral definida: `|\int_0^2 (6x-12) dx| + |\int_2^a (6x-12) dx|=|[3x^2-12x]_0^2|+|[3x^2-12x]_2^a=|3·2^2-12·2|+|3a^2-12a-(3·2^2-12·2)|=` `12+|3a^2-12a+12|` L'àrea de l'esquerra, `(0,2)` és negativa, per la qual cosa l'àrea de la dreta, `(a,2)` és positiva `=>` `12+3a^2-12a+12=3a^2-12a+24=15=> 3a^2-12a+9=0 => a^2-4a+3=0 =>` `a=(4 pm\sqrt{(-4)^2-4·3·1})/(2·1)=(4 pm\sqrt{4})/2=(4 pm\2)/2 => a_1=3` i `a_2=1` Com hem dit que `a>2` la solució és `a=3` ANNEX: (No ho demanen) Anem a veure la gràfica de l'àrea que hem calculat: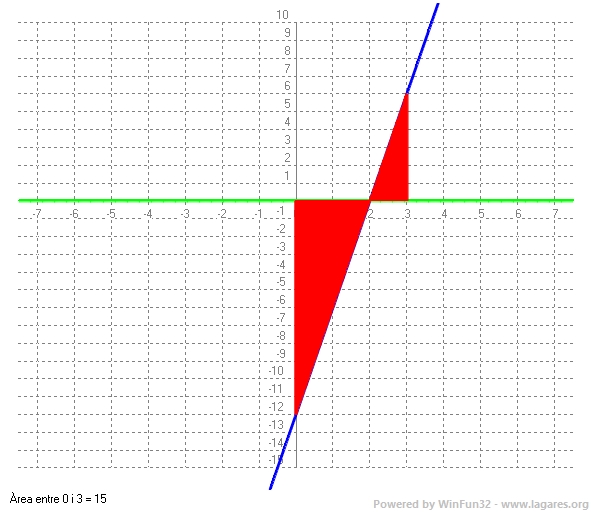