(2022-setembre-3-2)- Considereu la funció `f(x)=9/(x^2+x-2)`. a) Determineu el domini, les possibles asímptotes, els extrems relatius i els intervals de creixement i decreixement de la funció. [1,25 punts] b) Calculeu l’equació general de la recta tangent a la funció `f(x)` en el punt d’abscissa `x = 4`. Representeu en un mateix gràfic la funció `f(x)` i la recta tangent. [1,25 punts] SOLUCIÓ: a) Per trobar el domini, com és un quocient de polinomis està definit sempre excepte els `x` que fan que el denominador sigui `0`. `x^2+x-2=0 => x=(-1 pm \sqrt{(-1)^2-4·1·(-2)})/2=(-1 pm \sqrt{9})/2=(-1 pm 3)/2 => x_1=1` i `x_2=-2` Domini `R - {1,-2}` Que precisament aquests dos valors de les `x` són possibles candidats a haver-hi asimptotes verticals. `\lim_{x\to 1} 9/(x^2+x-2)=9/0= infty` `\lim_{x\to -2} 9/(x^2+x-2)=9/0= infty` Asímptotes verticals `x=1` i `x=-2` Per trobar, si n'hi ha, les asímptotes hortitzontals cal calcular: `\lim_{x\to pm infty}9/(x^2+x-2)=0` ja que el grau del polinomi de dalt, `0` `<` que el grau del polinomi de baix, `2`. Asímptota horitzontal `y=0` Com hi ha asímptota horitzontal tan cap a `pm infty` non'hi ha d'oblíqües. Per trobar els possibles extrems relatius caldrà calcular la derivada i igualar-la a `0`. `f'(x)= (-9(2x+1))/(x^2+x-2)^2=0 => 2x+1=0 => x=-1/2`. `f(1/2)=9/((-1/2)^2-1/2-2) = -4` Per saber si és un màxim o un mínim cercarem `f'(-1)` i `f'(0)` a l'esquerra i dreta del candidat a ser extrem `x=-1/2`. `f'(-1)= (-9(2*(-1)+1))/((-1)^2+(-1)-2)^2 = 2,25` `f'(0)= (-9(2*0+1))/(0^2+0-2)^2 = -2,25` A l'esquerra de `-1/2`, `f'(x)>0` i la dreta, `f'(x)<0 =>` que a `(-1/2,-4)` hi ha un màxim. Per trobar els inèrvals de creixement i decreixement resoldrem les inequacions, `f'(x)>0` i `f'(x)<0` `(-9(2x+1))/(x^2+x-2)^2>0` A sota és un quadrat, és sempre positiu per la qual cosa `-9(2x+1)>0` o sigui això serà positiu quan, `2x+1<0 => x<-1/2` per la qual cosa la funció serà creixent, `(-infty, -1/2) - {-2}`, treiem `x=-2` ja que no és del domini. Amb intèrvals, `(-infty, -2) cup (-2, -1/2)` `(-9(2x+1))/(x^2+x-2)^2<0` A sota és un quadrat, és sempre positiu per la qual cosa `-9(2x+1)<0` o sigui això serà negatiu quan, `2x+1>0 => x>-1/2` per la qual cosa la funció serà decreixent, `(-1/2, infty) - {1}`, treiem `x=1` ja que no és del domini. Amb intèrvals, `(-1/2, 1) cup (1, infty)` b) Per calcular la recta tangent en un punt cal calcula la imatge: `f(4)=9/(4^2+4-2) = 1/2` i el pendent: `m=f'(4)=(-9(2*4+1))/(4^2+4-2)^2 = -1/4` Podem escriure l'equció punt-pendent. `y-1/2=-1/4(x-4)` `4y-2=-x+4` Equació general de la recta:`x+4y-6=0` La explícita, no es demana, `y=-x/4+3/2`, però pot anar bé per fer la representació, que, sí es demana. La gràfica de la funció a partir de tot lo de l'apartat a: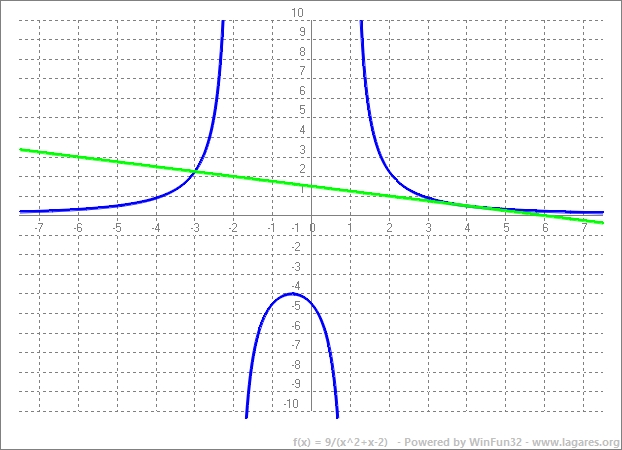