La Màgia de l'FFT

La sèrie de Fourier o desenvolupament de Fourier d'una funció f(x) versió exponencial complexa es defineix:

`f(x)=\sum_{n=-\infty}^\infty F(n)·e^((i2pinx)/N)`

On els coeficients de Fourier `F(n)` es calculen:

`F(n)=1/T_p\int_{-T_p/2}^(T_p/2) f(x)e^((-i2pikn)/N) dx`

Que en el cas discret es converteix:

`F(n)=1/N\sum_{k=0}^(N-1) f(k)e^((-i2pikn)/N)`

Exemple: Exponencial complexa - 4 valors

Si cada període té `4` valors, `{f(0), f(1), f(2), f(3)}`, l'anterior expressió queda:

`F(n)=1/4\sum_{k=0}^3 f(k)e^((-i2pikn)/4)`

`F(n)=1/4[f(0)e^((-j2pi·0·n)/4)+f(1)e^((-j2pi·1·n)/4)+f(2)e^((-j2pi·2·n)/4)+f(3)e^((-j2pi·3·n)/4)]`

O sigui `4·4=16` multiplicacions complexes i `4·3=12` sumes complexes. En general, si tenim `n` dades el nombre d0operacionss son aquestes. Algú podria pensar que n'hi ha menys que en la versió no exponencial complexa, cal recordar que son operacions amb nombres complexos.

Així si tenim `1024` dades, l'ordre de magnitud de les operacions que cal fer és de `1024^2 = 1048576`, més d'un milió. Per què he donat aquest nombre?, si fem l'análisi de les freqüències d'una veu mostrejada a `11025` mostres per segon, que no és de molt bona qualitat, `1024` mostres és aproximadament una dècima de segon de veu, que ja és de l'ordre de grandària de finestra que es fa servir.

Separar la suma per parells i imparellls

`F(n)=1/N[\sum_{k=0}^(N/2-1) f(2k)e^((-i2pi2kn)/N)+\sum_{k=0}^(N/2-1) f(2k+1)e^((-i2pi(2k+1)n)/N)]`

`F(n)=1/N[\sum_{k=0}^(N/2-1) f(2k)e^((-i2pikn)/(N/2))+e^((-i2pin)/N)·\sum_{k=0}^(N/2-1) f(2k+1)e^((-i2pikn)/(N/2))]`

Si ens fixem en l'última expressió veiem que hem convertit el càlcul dels coeficients de Fourier de `N` dades en el càlcul de dues sèries de Fourier, una pels valors de `f(k)` parells i una altra pels imparells. I això quina avantatge té? Suposem que la nostra funció té `16` dades, que pel que hem dit abans serien unes `16^2 = 256` multiplicacions. Si ho convertim en el càlcul de dues sèries de `8` dades, per cadascuna d'elles necesitarem `8^2 = 64` multiplicacions. Com tenim `2` sèries, caldrà fer el doble `64*2 = 128`. D'alguna manera hem pasat d'haver de fer `256` a `128` operacions. Si sabem com fer-ho, sembla que la reducció d'operacions és considerable, però `->`

Si a cada funció de `8` dades fem el mateix , és a dir, dividir per dues sèries amb els parells i imparells de les dues noves sèries caldrà fer `4` transformades de Fourier amb `4` dades cadascuna. O sigui per cadascuna d'elles caldrà fer `4*4 = 16` multiplicaions. Com tenim `4` series caldrà fer `16*4 = 64` operacions. Què passsa aquí? Hem passat de necessitar `256` operacions a `64`. I si arrivem a fer `8` transformades de Fourier de `2` dades cadascuna, llavors passariem a haver de fer `2^2*8 = 32` operacions.

Aquesta idea és la base de l'FFT, primer que el nombre de dades, `N` sigui una potència de `2` i calcular `log_2^N` (`16` dades hem dividit per `2`, `4=log_2^16` vegades) transformades de Fourier de `2` dades cadascuna. Es passa de `N^2` Càlculs a `N·log_2^N`.

Així si partim de `1024` dades passem de l'ordre de `1024^2 = 1048576` i fent servir l'FFT, per obtenir el mateix, `1024·log_2^1024=1024·10=10240` on s'aconsegueix una millora de `100` vegades menys.

DFT exponencial complexa - 2 - 4 - 8 valors - towards FFT

Funció amb `2` valors, `{f(0), f(1)}`

Funció amb `4` valors, `{f(0), f(1)}, f(2), f(3)}`

Funció amb `8` valors, `{f(0), f(1)}, f(2), f(3)}, f(4), f(5), f(6), f(7)`

Que si ens hi fixem en la primera columna:

És el mateix que es repeteix `4` vegades, que és el mateix que passa en la segona columna:

És el mateix que es repeteix `2` vegades i veiem que a la segona meitat passa exactament el mateix. Hi ha gran quantitat de càlculs repetits que només cal fer-los una vegada. D'aquí surten els "famosos" diagrames de papallona (butterfly diagrams).

Butterfly diagrams

Funció amb `2` valors, `{f(0), f(1)}`

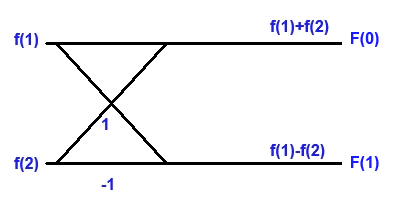Recordem que: `e^((-i2pik0)/2)=1` i `e^((-i2pik1)/2=-1)`

Funció amb `4` valors, `{f(0), f(1)}, f(2), f(3)}`

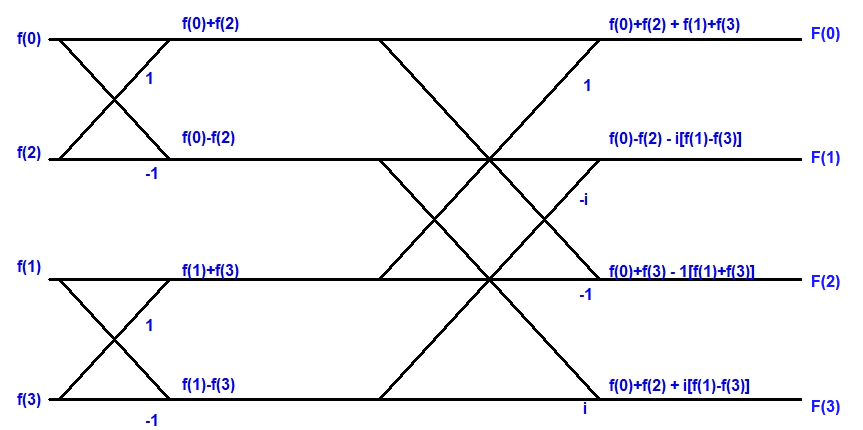Recordem que: `e^((-i2pik0)/4)=1` ; `e^((-i2pik1)/4)=-i` ; `e^((-i2pik2)/4)=-1` ; `e^((-i2pik3)/4)=i`

Funció amb `8` valors, `{f(0), f(1)}, f(2), f(3)}, f(4), f(5), f(6), f(7)`

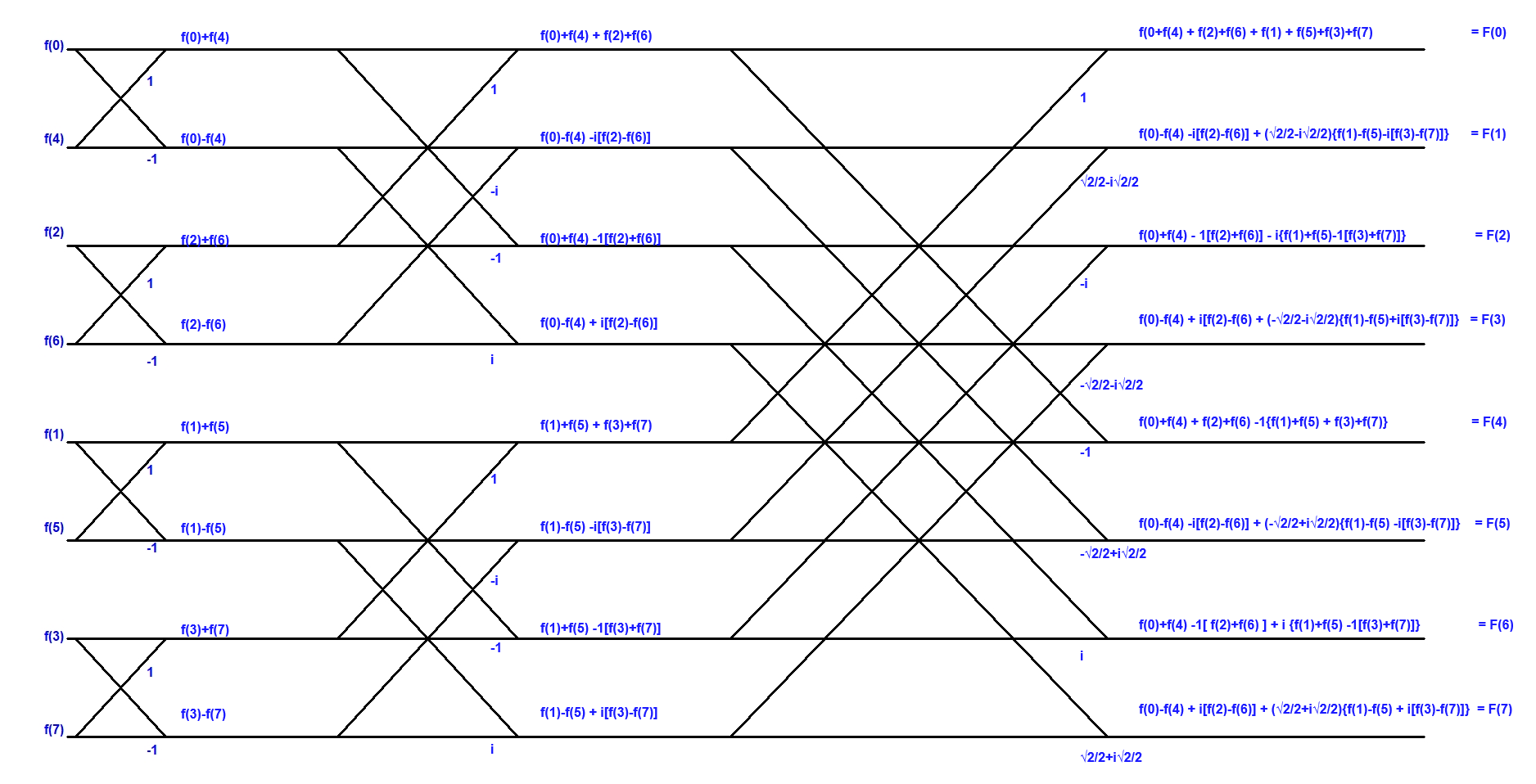Recordem que: `e^((-i2pik0)/8)=1` ; `e^((-i2pik1)/8)=\sqrt{2}/2-i\sqrt{2}/2` ; `e^((-i2pik2)/8)=-i` ; `e^((-i2pik3)/8)=-\sqrt{2}/2-i\sqrt{2}/2` ; `e^((-i2pik4)/8)=-1` ; `e^((-i2pik5)/8)=-\sqrt{2}/2+i\sqrt{2}/2` ; `e^((-i2pik6)/8)=i` ; `e^((-i2pik7)/8)=\sqrt{2}/2+i\sqrt{2}/2` ;

I ara el que cal és convertir això en un algorisme i escriure'l en un llenguatge informàtic. Afegir que tots el coeficients de baixada són `1`.