Informació per
al docent
FRECUENCIAS, VOCALES
Y TELÉFONOS
Información
general
-
Si se quiere producir un tono
puro es importante golpear el diapasón con un objeto relativamente
blando como un martillito de goma o un tapón de goma agujereado
colocado en el extremo de un bolígrafo. Los estudiantes no deben
golpearlo contra objetos duros, como el canto de una mesa ya que se producen
sobretonos y, además, se daña el diapasón.
-
Es conveniente utilizar diapasones
en el rango de 256 a 512 Hz. Se producen sobretonos fácilmente con
diapasones de frecuencias bajas. En un diapasón de frecuencia alta
los sobretonos se desvanecen rápidamente.
-
La mayor parte de diapasones
que se golpean con un objeto algo duro producen la frecuencia fundamental
y un sobretono relativamente importante.
-
En la experiencia se sugiere
que los estudiantes calculen la frecuencia determinando el periodo a partir
de dos ciclos adyacentes. Con ello se hace un error mayor que si se midiera
el tiempo que corresponde a un cierto número de ciclos y se dividiera
por este número.
-
Los experimentos que se sugieren
en las "Ampliaciones" son muy interesantes para los estudiantes que saben
algo de música. El profesor de música puede ayudarlos a "componer"
canciones con el marcador de tonos. Es un buen ejemplo de la relación
de la Física con otras materias.
Ejemplos de resultados
Primera Parte: Tonos
puros
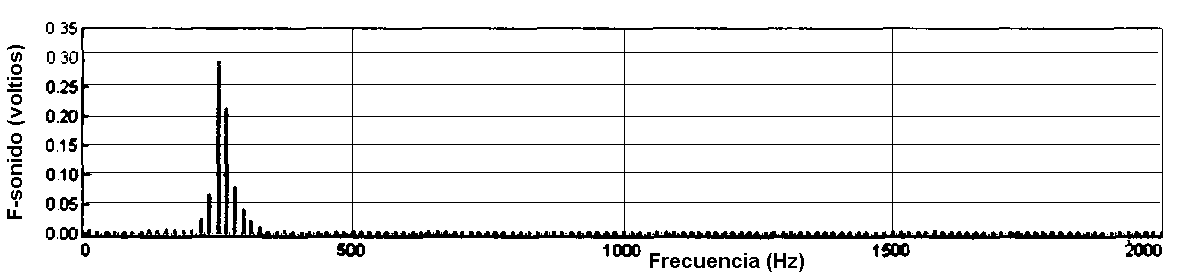
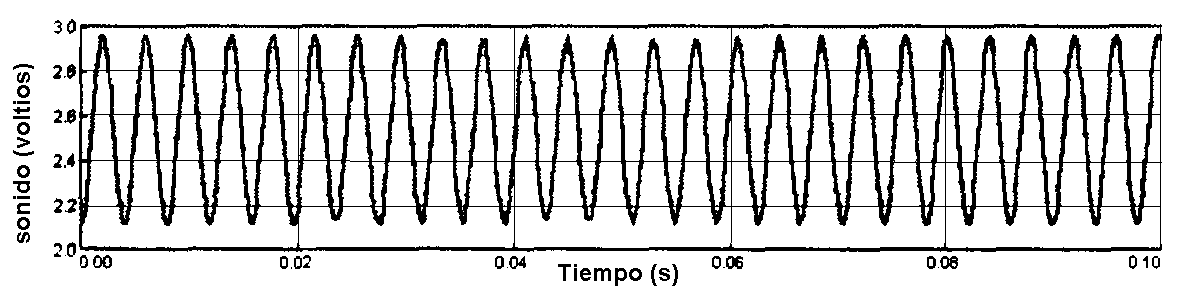
|
|
Diapasón 1
|
Diapasón 2
|
| Frecuencia
nominal del diapasón |
(Hz)
|
256
|
512
|
| Periodo
(experimental) |
(s)
|
0,00387
|
0,00175
|
| Frecuencia
(experimental) |
(Hz)
|
258
|
571
|
| Frecuencia
en el Análisis de Fourier |
(Hz)
|
250
|
516
|
Segunda parte: Sobretonos
en un diapasón de 256 Hz
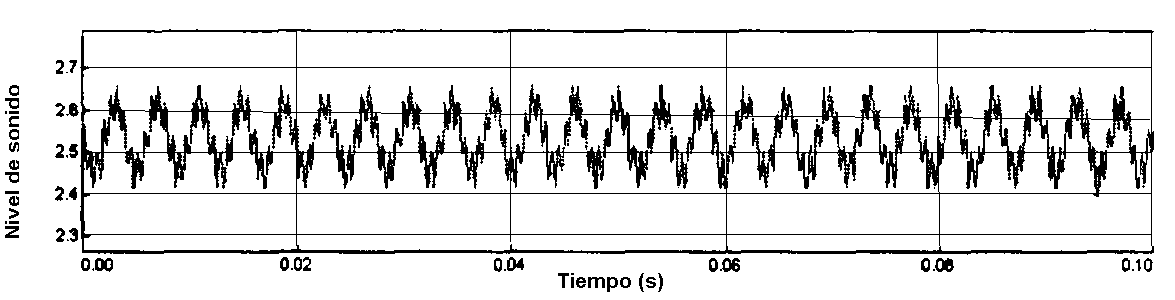
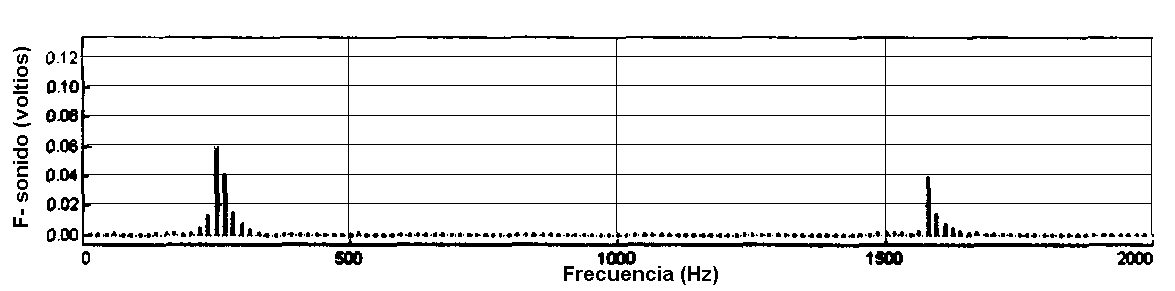
| Frecuencia
nominal del diapasón |
(Hz)
|
256
|
| Frecuencia
fundamental |
(Hz)
|
250
|
| Frecuencia
del sobretono |
(Hz)
|
1578
|
Tercera Parte: Análisis
de Fourier de dos vocales
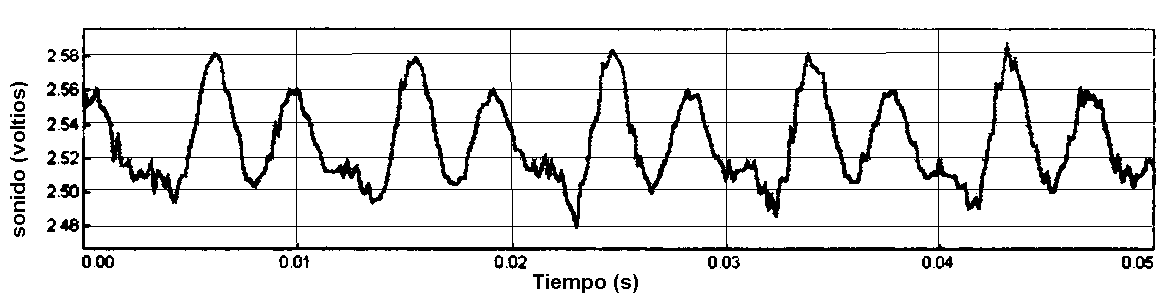
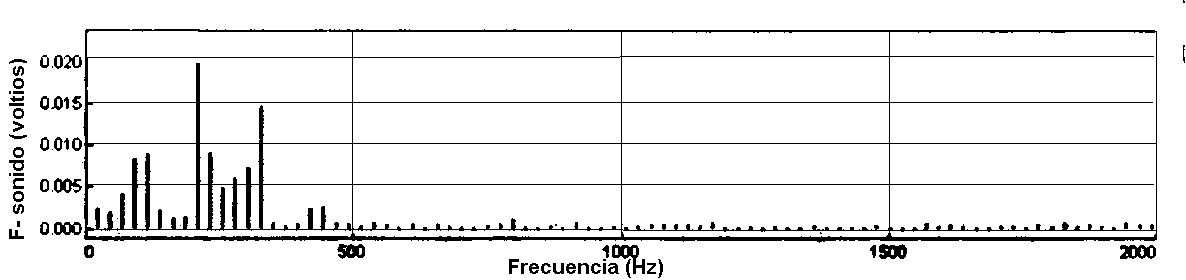
La vocal "e"
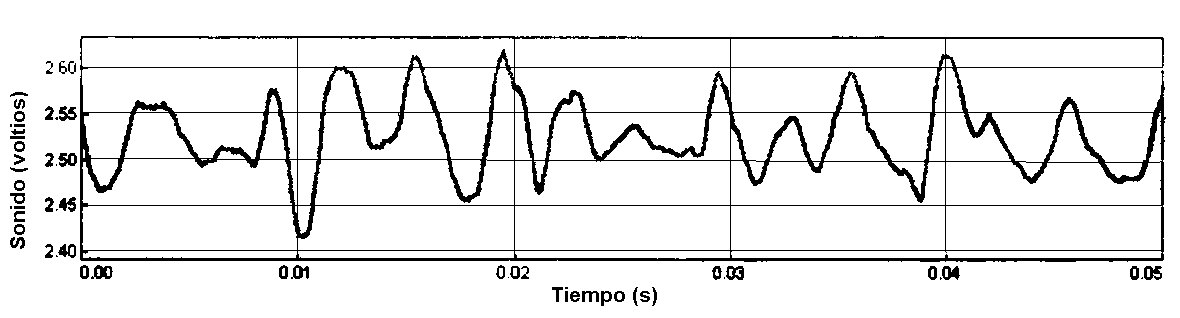
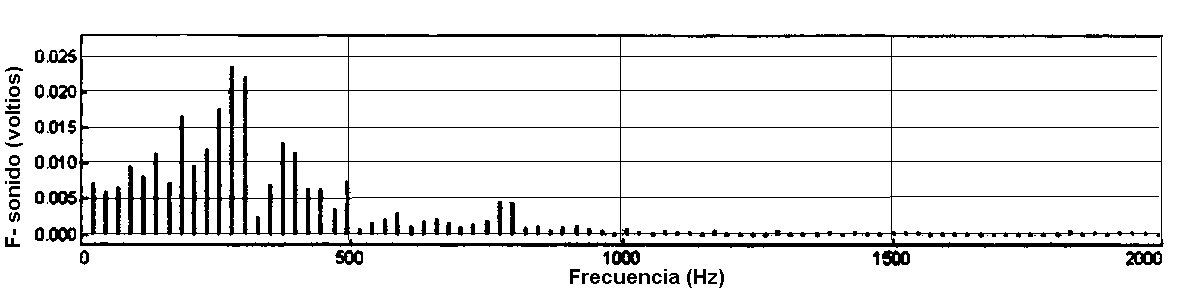
La vocal "o"
Cuarta Parte: Frecuencias
del dial de un teléfono de tonos
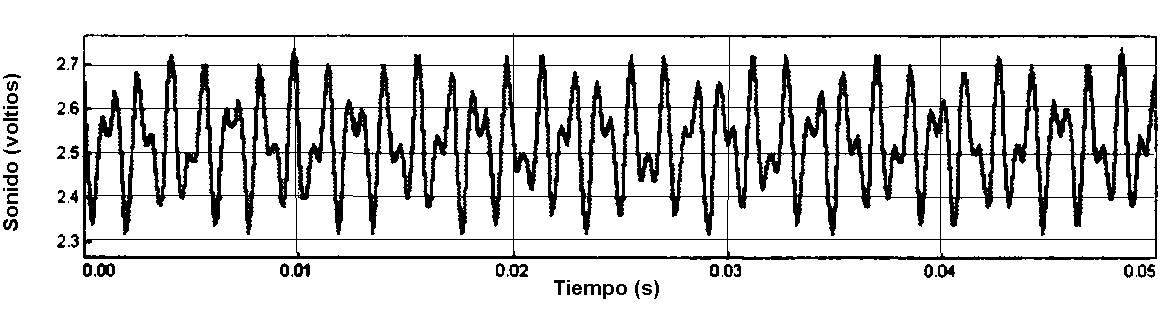
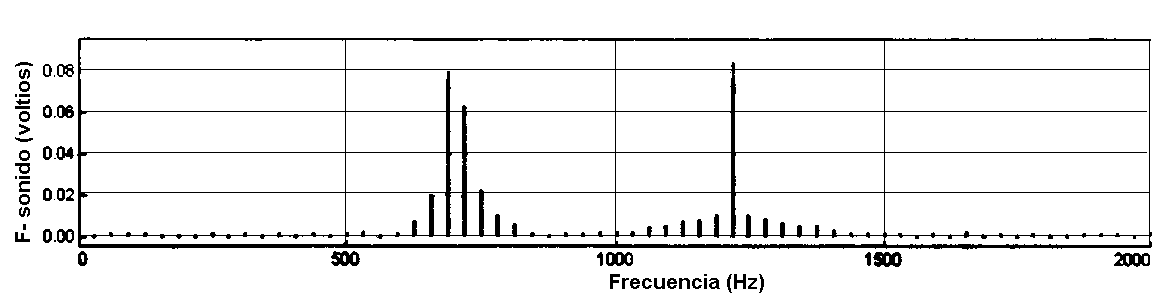
|
Botón
|
1
|
2
|
3
|
|
Baja Frecuencia (Hz)
|
688
|
688
|
688
|
|
Alta Frecuencia (Hz)
|
1203
|
1375
|
1461
|
|
Botón
|
4
|
5
|
6
|
|
Baja Frecuencia (Hz)
|
773
|
773
|
773
|
|
Alta Frecuencia (Hz)
|
1203
|
1375
|
1461
|
|
Botón
|
7
|
8
|
9
|
|
Baja Frecuencia (Hz)
|
859
|
859
|
859
|
|
Alta Frecuencia (Hz)
|
1203
|
1375
|
1461
|
Respuestas a las Cuestiones
iniciales
-
El diapasón parece simple
y tiene un sonido definido. El sonido del marcador telefónico de
tonos es más complejo.
-
El sonido correspondiente a
una nota que se tararea con la boca casi cerrada tiene un tono definido
como el de un diapasón, pero es más complejo.
-
Los tonos parecen incrementar
el tono al ir hacia la derecha y hacia abajo del teclado, pero es difícil
decidir si el tono del sonido del "7" es más agudo o grave que el
del "5".
-
El tono debe contener toda información
necesaria para poder decodificar los dígitos.
Respuestas del apartado
"Análisis de Datos"
-
Las frecuencias deben ser muy
parecidas.
-
El sonido de la "o" es más
brillante, con componentes importantes de alta frecuencia, que el sonido
de la "i", como muestran los gráficos de la sección anterior.
-
La tabla de datos muestra que
la frecuencia baja es la misma en las teclas de la misma fila pero aumenta
en filas sucesivas. La componente de frecuencia alta aumenta a lo largo
de las columnas sucesivas y es la misma en las teclas de la misma columna.
-
La compañía telefónica
detecta el número marcado a partir de las dos frecuencias principales
que forman el sonido de cada tecla.
Informació per
a l'estudiant
FRECUENCIAS, VOCALES
Y TELÉFONOS
Introducción
-
En este experimento podrás
analizar sonidos. Para ello usarás un micrófono conectado
al ordenador para obtener la forma de la onda correspondiente al sonido.
El proceso matemático llamado Análisis de Fourier (FFT: Fast
Fourier Transform) permitirá obtener las distintas frecuencias y
amplitudes cuya mezcla constituye los sonidos habituales.
-
En la primera parte del experimento
estudiarás el sonido de un diapasón que produce un sonido
formado esencialmente por una sola frecuencia. A continuarás observarás
como se producen sobretonos en un diapasón. Los sobretonos cuyas
frecuencias son múltiplos de un valor fundamental se llaman armónicos;
si no son múltiplos enteros son sobretonos inarmónicos. También
analizarás el sonido que corresponde a las vocales de tu voz. El
gráfico correspondiente al Análisis de Fourier te mostrará
como la voz esta formada por un número elevado de frecuencias individuales.
-
En la última parte del
experimento podrás resolver un problema. ¿Como sabe la compañía
telefónica el número que marcas? Los tonos que oyes en algunos
teléfonos cuando aprietas algunas teclas ¿contienen algún
tipo de código? Se puede resolver el problema y descubrir el código
utilizando uno de estos teléfonos, el micrófono y el Análisis
de Fourier.
Objetivos
-
Usar un micrófono para
analizar las frecuencias que forman el sonido de un diapasón y de
tu voz.
-
Comprobar que un diapasón
puede producir sobretonos.
-
Examinar el funcionamiento de
un marcador telefónico de tonos
Materiales
| Equipamiento
ExAO |
|
| Material
General de Laboratorio |
-
Dos diapasones (uno de 256 Hz
aprox.)
|
| Otros |
-
Marcador telefónico de
tonos
|
Cuestiones Iniciales
-
Golpea uno de los diapasones
con un martillito de goma (se puede hacer con un bolígrafo y un
tapón de goma de laboratorio). No golpees el diapasón con
materiales duros, que podrían dañarlo. Escucha el sonido.
Ahora aprieta un botón del marcador telefónico de tonos.
¿Cuál de los dos sonidos es más complejo? Justifica
tu respuesta.
-
Comparado con el sonido de un
diapasón y del marcador telefónico de tonos, el sonido de
una persona tarareando una nota ¿ es simple o complejo?
-
Aprieta los botones del marcador
de tonos. ¿Puedes observar algún orden en los tonos? ¿El
tono que corresponde a los números más grandes es más
agudo o está al azar?
-
¿Como crees que la compañía
telefónica reconoce los números que marcas?
Procedimiento
-
Conecta el micrófono
a la entrada 1 de la interface
-
Calibración de
los sensores
-
No es necesario un calibrado.
Si la captación muestra una señal poco intensa se debe acercar
el micrófono a la fuente de sonido.
-
Parámetros de la
captación
-
Prepara la captación
activando las opciones del menú: Captación/Captación
modo PC/Rápida. Cuando aparezca la ventana para definir los parámetros
de la captación, selecciona:
-
1000 muestras, que corresponden
a una captación con una duración total de 0,05 s.
-
Captación inmediata
No aprietes el botón
"Aceptar" hasta que quieras iniciar la captación.
Ejecución y tratamiento
matemático inicial
Primera Parte: Tonos puros
-
Golpea un diapasón con
un martillo de goma y sosténlo junto al micrófono. Aprieta
el botón "Aceptar" para empezar la captación. Si el diapasón
se golpea demasiado fuerte se crean sobretonos o una mezcla de frecuencias
más elevadas, además de la frecuencia principal.
-
Imprime o dibuja el gráfico
que obtengas.
-
Mediante la opción Representación/Niveles
(selecciona el tiempo) mide el intervalo medio de tiempo (periodo) correspondiente
a un ciclo, entre picos adyacentes. Anota este valor en la tabla de datos.
-
Calcula la frecuencia y anótala
en la tabla de datos.
-
Utiliza la opción Útiles/Análisis
de Fourier, y selecciona el número de armónicos que se calcularán
(256). Ajusta el cursor en la posición en la que empezará
el Análisis de Fourier de los datos. Con la opción: Representación/Punto
a Punto podrás medir la frecuencia predominante en el análisis.
Anota el valor.
-
Repite las etapas 3-8 con el
segundo diapasón.
Segunda parte: Sobretonos
en un diapasón
-
En esta etapa se trata de hacer
que un diapasón de 256 Hz produzca un sobretono. Esta vez, golpea
el diapasón con un nudillo y escucha el sonido. Describe la diferencia.
-
Prepara la captación
tal como se explica en el apartado 3. Golpea de nuevo el diapasón
con el nudillo y sostenlo cerca del micrófono. Aprieta el botón
"Aceptar" para empezar la captación.
-
Compara la forma de la onda
y el Análisis de Fourier de este sonido con el de la primera parte.
Mediante la opción: Representación/Punto a Punto mide la
frecuencia fundamental y la del primer sobretono. Anota los valores en
la tabla de datos.
Tercera Parte: Análisis
de Fourier de dos vocales
-
Hay una adquisición como
en los apartados precedentes y captura el sonido de la vocal "i" con el
micrófono cerca de la boca. Haz el Análisis de Fourier de
este sonido. Imprime o dibuja los gráficos correspondientes a la
onda sonora y a su análisis.
-
Repite el paso anterior, esta
vez con la vocal "o".
Cuarta Parte: Frecuencias
de un marcador de tonos
-
En esta parte del experimento
analizarás el sonido de un marcador telefónico de tonos al
marcar. Coloca el altavoz del marcador cerca del micrófono y haz
la captación correspondiente al sonido de la tecla "1" del teléfono.
Analiza las frecuencias presentes en este sonido y anota el valor de las
dos frecuencias predominantes.
-
Repite el paso anterior con
los números del "2" al "9" del teclado.
Tabla de Datos
Primera Parte: Tonos
puros
|
|
Diapasón 1
|
Diapasón 2
|
| Frecuencia
nominal del diapasón |
(Hz)
|
|
|
| Periodo
(experimental) |
(s)
|
|
|
| Frecuencia
(experimental) |
(Hz)
|
|
|
| Frecuencia
en el Análisis de Fourier |
(Hz)
|
|
|
Segunda parte: Sobretonos
en un diapasón
| Frecuencia
nominal del diapasón |
(Hz)
|
|
| Frecuencia
fundamental |
(Hz)
|
|
| Frecuencia
del sobretono |
(Hz)
|
|
Cuarta Parte: Frecuencias
de un marcador telefónico de tonos
|
Botón
|
1
|
2
|
3
|
|
Baja Frecuencia (Hz)
|
|
|
|
|
Alta Frecuencia (Hz)
|
|
|
|
|
Botón
|
4
|
5
|
6
|
|
Baja Frecuencia (Hz)
|
|
|
|
|
Alta Frecuencia (Hz)
|
|
|
|
|
Botón
|
7
|
8
|
9
|
|
Baja Frecuencia (Hz)
|
|
|
|
|
Alta Frecuencia (Hz)
|
|
|
|
Análisis de
Datos
-
En cada diapasón, compara
la frecuencia calculada a partir de las medidas en la onda sonora, la que
se obtiene en el Análisis de Fourier y la que figura escrita en
el propio diapasón.
-
Describe la diferencia en las
frecuencias que forman las dos vocales que has estudiado en la Tercera
Parte..
-
Examina los datos que corresponden
al marcador teléfono de tonos ¿Que tendencia observas?
-
Resume el modo con que la compañía
telefónica determina los números que se aprietan al marcar.
Ampliaciones
-
Utiliza el micrófono
para examinar las formas de las ondas de las notas de distintos instrumentos
musicales. ¿Qué instrumentos producen tonos puros? ¿La
nota Do de un instrumento tiene la misma frecuencia que la nota Do de otro?
¿Cambia la forma de la onda con la intensidad del sonido? ¿Cambia
la forma de la onda al cambiar la frecuencia?
-
Si dispones de un órgano
electrónico, utiliza el micrófono y un análisis similar
a los experimentos que has realizado para determinar qué teclas
tienen frecuencias más cercanas a las que corresponden a tu número
de teléfono. Escribe la secuencia de notas musicales que corresponden
a tu número de teléfono. Toca tu número de teléfono
en el órgano.
-
Analiza las tres vocales restantes
(a, e, u). Intenta buscar un método para producir las distintas
vocales combinando sobretonos, del modo en que se genera una voz artificial.
-
Continúa la investigación
sobre el teclado de tonos incluyendo la última fila de teclas: *,
0 y #. El patrón correspondiente al resto de teclas ¿También
funciona con estas?
|









