Informació per
al docent
LAS
MATEMÁTICAS DE LA MÚSICA
Información
general
-
Los sonidos simples funcionan
mejor para estos experimentos. Cuando más parecido sea el sonido
al que corresponde a una onda senoidal, más simple será su
Análisis de Fourier y más evidente resultará la frecuencia
fundamental. Se recomienda emplear órganos electrónicos baratos
seleccionando el sonido tipo "flauta", sin vibrato. Instrumentos tales
como flautas o trompetas también funcionan bien; se debe mantener
el tono constante al analizar cada nota.
-
En estos experimentos los estudiantes
descubrirán regularidades en las frecuencias de las notas de una
escala musical. Al menos hay dos regularidades que pueden descubrir. Si
se concentran en la escala diatónica (teclas blancas, empezando
con el Do), deberían descubrir que todas las notas tienen relaciones
simples de frecuencias respecto la de la primera nota:
Re: 1 + 1/8 = 9/8 La:
1 + 2/3 = 5/3
Mi: 1 + 1/4 = 5/4 Si: 1 +
7/8 = 15/8
Fa: 1 + 1/3 = 4/3 Do: 2 =
2/1
Sol: 1 + 1/2 = 3/2
Un instrumento musical afinado
con estas relaciones tiene afinación justa.
-
Si estudian todas las notas
de la escala cromática (teclas blancas y negras empezando con Do),
los estudiantes pueden descubrir que la relación de la frecuencia
de una nota con la de la anterior es siempre la misma. Muchos instrumentos
musicales se afinan de esta manera y esta afinación se denomina
temperada. Un instrumento afinado de esta manera es más fácil
de usar en diferentes tonalidades y permite transportar fácilmente
una composición de una tonalidad a otra. Cada nota tiene una frecuencia
21/12= 1,0594 veces mayor que la nota anterior. El intervalo
de una nota a la siguiente se llama semitono. El intervalo de una nota
hasta la misma nota en la octava siguiente contiene 12 semitonos.
-
La afinación temperada
es un compromiso que funciona bien. Permite recorrer una octava de la escala
cromática en 12 pasos iguales lo que supone muchas ventajas para
los músicos. En la afinación temperada las frecuencias que
corresponden a las notas de la escala diatónica son muy parecidas
a las que les corresponden en la afinación justa.
-
Algunos instrumentos se afinan
con afinación justa pero se han de usar en una tonalidad determinada.
Por ello, la afinación de la inmensa mayoría de instrumentos
modernos es temperada.
-
La música se basa en
relaciones. La misma relación de frecuencias provoca la misma sensación,
tanto si ocurre en un rango de frecuencias bajas como de frecuencias altas.
-
La tabla que se da como ejemplo
contiene una columna adicional que se ha llamado "Relación respecto
C4 para afinación justa": Es la relación que se
esperaría si el instrumento, en vez de tener afinación temperada
tuviera afinación justa.
-
En la discusión no se
han tenido en cuenta los efectos fisiológicos del sistema auditivo
en la afinación. Estos efectos fisiológicos hacen que, a
veces, se prefieran octavas algo estiradas, es decir, con una relación
de frecuencias algo mayor de 2.
Ejemplos de resultados
|
Tecla
|
Nota
|
Frecuencia
(Hz)
|
D
f
(Hz)
|
Relación con
la nota anterior
|
Relación (experimental)
con C4
|
Relación con
C4 para afinación justa
|
|
1
|
Do4
|
263
|
|
|
1.00
|
1,00
|
|
2
|
Do4#
|
279
|
16
|
1,06
|
1,06
|
|
|
3
|
Re4
|
295
|
16
|
1,06
|
1,12
|
1,12 (1 1/8)
|
|
4
|
Mi4b
|
314
|
19
|
1,06
|
1,19
|
|
|
5
|
Mi4
|
330
|
16
|
1,05
|
1,25
|
1,25 (1 1/4)
|
|
6
|
Fa4
|
352
|
22
|
1,07
|
1,34
|
1,33 (1 1/3)
|
|
7
|
Fa4#
|
373
|
21
|
1,06
|
1,42
|
|
|
8
|
Sol4
|
395
|
22
|
1,06
|
1,50
|
1,50(1 1/2)
|
|
9
|
La4b
|
419
|
24
|
1,06
|
1,59
|
|
|
10
|
La4
|
443
|
24
|
1,06
|
1,68
|
1,66 (1 2/3)
|
|
11
|
Si4b
|
470
|
27
|
1,06
|
1,79
|
|
|
12
|
Si4
|
497
|
27
|
1,06
|
1,89
|
1,87 (1 7/8)
|
|
13
|
Do5
|
526
|
29
|
1,06
|
2,00
|
2,00
|
|
17
|
Mi5
|
662
|
|
|
2,52
|
2,5
|
|
20
|
Sol5
|
791
|
|
|
3,01
|
3,00
|
|
25
|
Do6
|
1056
|
|
|
4,02
|
4,00
|
Respuestas a las Cuestiones
iniciales
-
Frecuencia
-
Amplitud
-
Puede haber distintas respuestas.
Puede ocurrir que algún alumno en un grupo sepa música y
sepa qué se debe esperar en el experimento.
Respuestas del apartado
"Análisis de Datos"
-
Las diferencias en las frecuencias
de las notas aumentan gradualmente. No se ve una regularidad.
-
Él valor de cada relación
es prácticamente 1,06 ó, aproximadamente 21/12.
-
Las notas de la escala diatónica
tienen frecuencias cuya relación con la frecuencia de la nota C4
se pueden expresar como:
Do: 1 = 1/1 Sol: 1 +
1/2 = 3/2
Re: 1 + 1/8 = 9/8 La: 1 +
2/3 = 5/3
Mi: 1 + 1/4 = 5/4 Si: 1 +
7/8 = 15/8
Fa: 1 + 1/3 = 4/3 Do: 2 =
2/1
-
Cada nota sucesiva de la escala
cromática incrementa su frecuencia en un factor 1,06
-
Frecuencias: Do3=
mitad de la frecuencia de Do4; Do6= doble de la frecuencia
de Do5; Re5= doble de la frecuencia de Re4
-
Las frecuencias de dos notas
que forman una "tercera" están en la relación 5:4; las "octavas"
corresponden a una relación 2:1; Fa4 y Do4
son una "cuarta" y su relación es 4:3.
Respuestas del apartado
Amplicaciones
-
Si el experimento se hace empezando
con otra tecla, las notas que corresponden a la escala diatónica
en esta nueva tonalidad deben modificarse con los sostenidos o bemoles
correspondientes.
-
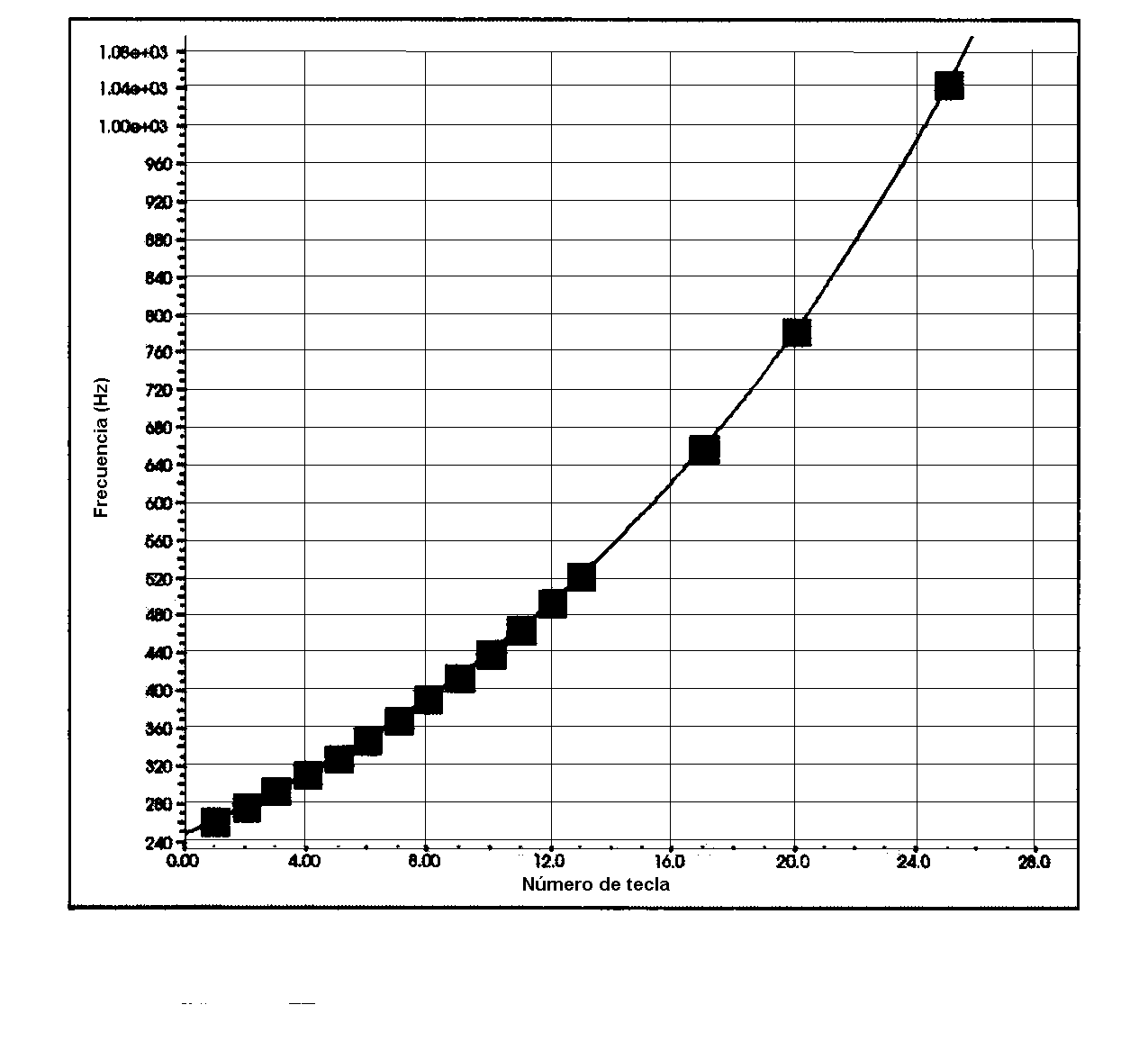
La gráfica corresponde
a los datos de la tabla que se ha dado como ejemplo. La curva que ajusta
a los datos es una exponencial f= 247 e0,0577n. Es interesante
constatar que e0,0577 =1,0594 =21/12. Una función
21/12 n doblará su valor a cada valor de n múltiplo
de 12, tal como sucede cada 12 teclas del órgano.
-
Quizá los estudiantes
podrán encontrar otro instrumento preparado para tocar en una sola
tonalidad, con afinación justa. Algunos "instrumentos" formados
por tubos metálicos que se golpean están afinados de este
modo.
-
Internet puede resultar útil
para encontrar las relaciones de frecuencias que corresponden a instrumentos
de otras culturas.
Informació
per a l'estudiant
LAS MATEMÁTICAS
DE LA MÚSICA
Introducción
-
La escala musical que es usa
en la música occidental se originó en la antigua Grecia.
Originalmente, una escala tenía siete notas. Esta es la escala diatónica
e incluso los que no saben música conocen los nombres de las
notas: do-re-mi-fa-sol-la-si-do. Esta escala corresponde a las notas sucesivas
de las teclas blancas de un piano, empezando por el Do. La octava tecla
vuelve a ser un Do y, por ello, este rango de notas se llama octava.
-
Al transcurrir el tiempo se
añadieron cinco notas más a la escala musical occidental.
Globalmente, esta escala de 12 notas se llama escala cromática.
En una escala que empiece en la tecla Do de un piano, las 5 notas extra
corresponden a las teclas negras.
-
Las escalas musicales están
estrechamente relacionadas a las matemáticas. En este experimento
usarás un micrófono conectado a una interface, que a su vez
está conectada a un ordenador, para registrar las formas de la ondas
sonoras de las notas musicales. El ordenador hará el análisis
matemático llamado Análisis de Fourier para determinar la
frecuencia fundamental del sonido. Deberás medir las frecuencias
de todas las notas de la escala cromática y buscar el modelo matemático
que corresponde a estas frecuencias.
-
Las frecuencias de dos notas
que al sonar al mismo tiempo dan un sonido agradable, normalmente, tienen
una relación matemática especial. En esta experiencia también
estudiarás las relaciones matemáticas que hay en los intervalos
que son usuales en música.
Para esta experiencia
se recomienda un órgano electrónico, pero se pueden usar
otros instrumentos.
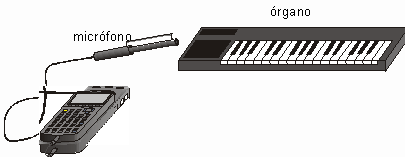
Figura 1
Objetivos
-
Determinar las frecuencias de
las notas de la escala musical.
-
Examinar las diferencias y las
relaciones entre estas notas.
-
Estudiar los modelos matemáticos
que se usan en las escalas.
Materiales
| Equipamiento
ExAO |
|
| Material
General de Laboratorio |
|
| Otros |
-
Órgano electrónico
(u otro instrumento)
|
Cuestiones Iniciales
-
¿Qué concepto
físico está más estrechamente relacionado con lo que
los músicos conocen como altura del sonido?
-
¿Qué concepto
físico está estrechamente relacionado con la intensidad sonora
de una nota musical?
-
Elabora una hipótesis
sobre la relación entre las frecuencias de las notas de la escala
diatónica (do-re-mi...). ¿Crees que cada nota tiene un número
concreto de Hz por encima de la nota precedente? ¿Crees que cada
nota sucesiva tiene una frecuencia más alta en un factor constante
respecto la nota precedente? ¿Qué sucede con las frecuencias
en la escala cromática completa?
Procedimiento
-
Conecta el micrófono
a la entrada 1 de la interface.
-
Colocación de los
sensores
-
Coloca el micrófono cerca
del altavoz del órgano.
-
Calibración de
los sensores
-
No es necesario un calibrado.
Si la captación que se va a realizar muestra una señal poco
intensa se debe acercar el micrófono al altavoz.
-
Parámetros de la
captación
-
Prepara la captación
activando las opciones del menú: Captación/Captación
modo PC/Rápida. Cuando aparezca la ventana para definir los parámetros
de la captación, selecciona:
-
1000 muestras, que corresponden
a una captación con una duración total de 0,05 s.
-
Captación inmediata
No pulses el botón
[Aceptar] hasta que quieras iniciar la captación.
-
Ejecución y tratamiento
matemático inicial
-
Aprieta la primera tecla que
vas a estudiar: el Do medio (su frecuencia debería ser de 262 Hz,
aproximadamente). En un teclado de un pequeño órgano esta
puede ser la primera nota. Mientras suena la nota aprieta el botón
"Aceptar" para hacer la captación.
-
Utiliza la opción: Útiles/Análisis
de Fourier, y selecciona el número de armónicos que se calcularán
(256). Ajusta el cursor en la posición en la que empezará
el Análisis de Fourier de los datos. Con la opción: Representación/Punto
a Punto podrás medir el valor de la frecuencia más baja en
el análisis, que se denomina frecuencia fundamental. Anota
el valor en la tabla de datos.
-
Repite los pasos 4-6 para cada
nota de la Tabla de Datos. Las notas 1 a 12 de la figura 2 corresponden
a una octava completa. Las notas 13, 17, 20 y 25 de la figura corresponden
a octavas superiores. Si no sabes música la Figura 2 te será
útil para localizar las notas que se deben analizar (en la tabla
de datos cada nota tiene el número que le corresponde en el teclado).
Tabla de Datos
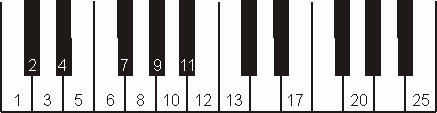 Figura 2
Figura 2
|
Tecla
|
Nota
|
Frecuencia f (Hz)
|
D
f (Hz)
|
Relación con
la nota anterior
|
Relación con
C4
|
|
1
|
Do4
|
|
|
|
1,0
|
|
2
|
Do4#
|
|
|
|
|
|
3
|
Re4
|
|
|
|
|
|
4
|
Mi4b
|
|
|
|
|
|
5
|
Mi4
|
|
|
|
|
|
6
|
Fa4
|
|
|
|
|
|
7
|
Fa4#
|
|
|
|
|
|
8
|
Sol4
|
|
|
|
|
|
9
|
La4b
|
|
|
|
|
|
10
|
La4
|
|
|
|
|
|
11
|
Si4b
|
|
|
|
|
|
12
|
Si4
|
|
|
|
|
|
13
|
Do5
|
|
|
|
|
|
17
|
Mi5
|
|
|
|
|
|
20
|
Sol5
|
|
|
|
|
|
25
|
Do6
|
|
|
|
|
Análisis de
Datos
-
Calcula la diferencia entre
las frecuencias de una nota y de la anterior (excepto la primera y las
tres últimas de la tabla). Anota tus resultados en la columna D
f (Hz) de la tabla de datos. ¿Cómo son los valores que has
calculado, a lo largo de la octava?
-
Calcula el cociente (relación)
entre cada frecuencia y la anterior (excepto la primera y las tres últimas
de la tabla). Anota tus resultados en la tabla de datos. ¿Cómo
son los valores que has calculado, a lo largo de la octava?
-
Completa los espacios que no
están sombreados de la última columna de la Tabla de Datos
con la relación de la frecuencia de la nota correspondiente con
la frecuencia de la nota Do4.
-
Estudia los datos que corresponden
a las teclas blancas del órgano (escala diatónica). Estas
notas están en letra negrita en la Tabla de Datos. Trata de identificar
alguna regularidad entre las relaciones de sus frecuencias. Las relaciones
de la última columna pueden reducirse a relaciones entre números
enteros pequeños. ¿Cuales serían las relaciones de
números enteros correspondientes? (por ejemplo, la relación
1,33 corresponde al cociente 4/3).
-
Si se consideran todas las notas
¿qué regularidad hay entre notas sucesivas? Justifícalo
a partir de los datos de tus experimentos.
-
Basándote en tus datos
haz una predicción de las frecuencias de las notas: Do3,
Do7 y Re5.
-
Las notas Mi4 y Do4
constituyen una "tercera" musical y el sonido conjunto de las dos notas
resulta agradable. Lo mismo ocurre con el sonido de Sol4 y Do4
que son una "quinta", y con Do5 y Do4 que son una
"octava". ¿Qué relación de números enteros
caracteriza estos intervalos musicales? ¿ Crees que todas las terceras,
quintas u octavas tendrán la misma relación de números
enteros?
Ampliaciones
-
Repite las mismas medidas empezando
en una tecla distinta de Do4, calculando todas las relaciones
respecto esta nueva tecla.
-
Si se numeran las teclas como
en la figura 2, se puede hacer una gráfica de la frecuencia en función
del número correspondiente a la tecla. Ajusta una curva a estos
datos. ¿Qué ecuación corresponde a esta gráfica?
¿Cómo interpretas esta ecuación?
-
Investiga los distintos tipos
de afinación de instrumentos musicales: Justa, Temperada, Pitagórica,
Diatónica. Estudia las frecuencias de un instrumento musical que
utilice un sistema de afinación completamente distinto de estos,
como los del Sudeste de Asia.
|


