Las funciones trigonométricas
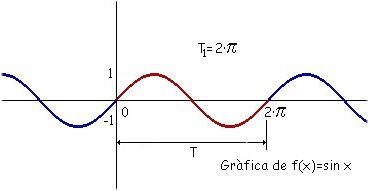
Las funciones trigonométricas sirven como modelo pera expresar matemáticamente las características de las ondas sonoras. Es por eso que vamos a hacer un pequeño estudio de sus propiedades. Comencemos per la más simple: La función f(x)=sin x tiene la representación gráfica siguiente:
La gráfica de la función se repite al incrementar o disminuir
el valor de x. A partir de la que se encuentra en el intervalo [0,
2 Esto es debido a la propiedad siguiente: sin x = sin (2
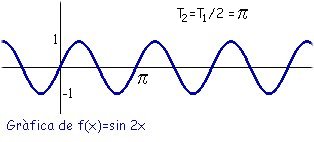
Pero, que pasará si aumentamos el valor que multiplica a la x? Tomemos, por ejemplo, la función f(x) = sin 2x
En este caso, el periodo es la mitad del de la función anterior,
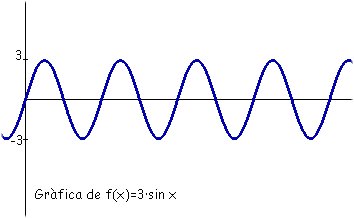
es decir Físicamente, diremos que su frecuencia es el doble que la anterior. Si, en cambio, multiplicamos sin x por un número cualquiera observaremos que la función experimenta unos cambios diferentes. Consideremos la función f(x) = 3 sin x:
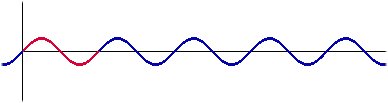
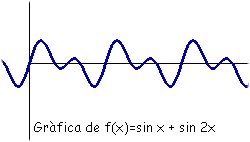
Gráficamente, ha sufrido una deformación. Ha habido un estiramiento en dirección vertical. El periodo continúa siendo el mismo que el de la función f(x) = sin x, es decir, la onda continúa teniendo la misma longitud pero podemos ver que ha aumentado su amplitud de onda (A). En el lenguaje musical diremos que ha aumentado su intensidad. Veamos que pasa cuando sumamos dos funciones del tipo f(x) = sin ax como, por ejemplo, f(x)=sin x + sin 2x
La función continúa teniendo el mismo periodo (2 Observación: Las funciones del tipo f(x)=sin nx, donde n es un
número natural, como las que hemos visto anteriormente, siempre
tendrán como periodo 2
Si queremos expresar una función trigonométrica de periodo
T,
esta vendrá dada por la expresión: f(x)=sin (2 Igualmente, con las funciones del tipo f(x)=sin nx + sin mx,
el periodo será 2 Ejemplo: f(x)=sin x + sin 2x + sin 3x Sabiendo que el M.C.D.
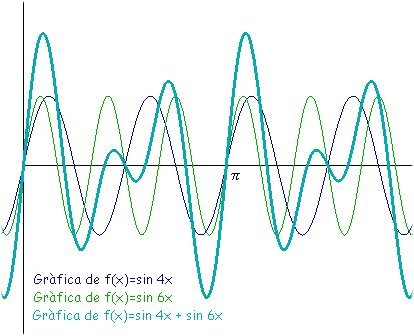
de 1, 2 y 3 es 1, podemos deducir que su periodo será 2 Por tanto, si en una función del tipo f(x)=sin ax le sumamos funciones del tipo f(x)=sin k·ax el periodo (y, por tanto, la frecuencia) continúa siendo el mismo. Ejemplo: f(x)=sin 4x + sin 6x. Sabiendo que el M.C.D. de
4 y 6 es 2, podemos deducir que su periodo será 2 Gráficas de sin 4x, de sin 6x y de sin
4x + sin 6x
De la misma forma, si a una función del tipo f(x) = sin ax le sumamos funciones del tipo f(x) = sin k·ax con amplitud cada vez más pequeña nos aparecerán modelos de ondas parecidas a les producidas por los instrumentos musicales. Estos múltiplos que se le sumen a la onda primaria reciben el nombre de armónicos. Cada sonido instrumental tendrá una forma de onda determinada debido a la variedad de los armónicos que se le han añadido a la onda principal, lo que nos permitirá reconocer de que instrumento procede. En el lenguaje musical, este fenómeno recibe el nombre de timbre. |