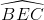4. Centres i propietats relacionades
La paraula centre no defineix
un únic concepte, ni tan sols en el camp de la geometria. El diccionari
de
l’Institut d’Estudis Catalans, per exemple, dóna tres accepcions
interpretables
geomètricament que són força diferents:
- Punt al voltant del qual tots els punts del
contorn d’un cos o figura estan disposats de manera que cada dos
situats en un mateix diàmetre equidisten d’aquell.
- La part d’una cosa més allunyada de la perifèria.
- Punt d’aplicació de la resultant de diferents
forces que obren sobre un cos.
La primera definició no seria
aplicable a un triangle qualsevol, ja que no existeix un centre per on
passen
infinits diàmetres amb un parell de punts equidistants pertanyents al
triangle. La segona, en canvi, coincideix amb la definició de
l’incentre (vegeu 4.2.).
I la tercera, tot i no ser
estrictament matemàtica, si es considera el triangle com un cos
material i
homogeni, es pot interpretar com el baricentre (vegeu 4.1.), en ser
el centre
de masses.
Actualment, en l’estudi del triangle
s’han catalogat una gran quantitat d’elements i punts notables. L’Enciclopèdia
de Centres de Triangle (Encyclopedia of Triangle
Centers – ETC pel
seu nom en anglès), després de seleccionar els punts que eren prou
rellevants,
estaven ben definits, i encaixaven amb la definició matemàtica de centre
del triangle
actualment acceptada (que es pot consultar des de la pròpia
enciclopèdia) ha
publicat a la xarxa una relació amb més de 3.500 centres diferents, i
és una
llista que encara s’actualitza periòdicament.
Ara bé, existeixen quatre centres
molt destacats que ja es coneixien des de l’antiguitat: el baricentre,
l'incentre, el circumcentre i l'ortocentre.
4.1. Baricentre
El baricentre (G) és el punt
d’intersecció de les tres mitjanes d’un triangle, que són els segments
que
uneixen cada vèrtex amb el punt mitjà del costat oposat. La demostració que les tres mitjanes són
concurrents és un
corol·lari del teorema de Ceva (vegeu 5.3.).
El
baricentre té les següents propietats:
- Sempre se situa a l'interior del triangle.
- Se situa al doble de distància del vèrtex que del
punt mitjà del costat. Per tant, respecte a la longitud de la mitjana,
se situa a dues terceres parts del vèrtex i a una tercera
part del punt mitjà del costat.
- Un triangle definit pels tres punts mitjans dels
costats d'un altre triangle, tindrà el mateix baricentre que aquest
últim.
- Cada mitjana parteix el triangle en dues parts que
tenen la mateixa àrea. Per aquesta raó, el baricentre
correspondria
al
centre de gravetat d’un cos físic triangular amb massa uniformement
distribuïda per la superfície.
- Les tres mitjanes tallen el triangle en sis parts
que tenen la mateixa àrea.
4.2. Incentre
L’incentre (I) és el punt
d’intersecció de les tres bisectrius d’un triangle, que són els
segments que divideixen cada angle en dues parts iguals. Té les
següents propietats:
- Sempre està
situat a l’interior
del triangle.
- És
centre de la
circumferència inscrita, ja que les bisectrius són els llocs geomètrics
equidistants a dos costats, i el punt on se'n tallen dues
és
equidistant als tres. Així demostro que la tercera bisectriu,
com
que també ha de ser equidistant als seus dos costats, concorre en el
mateix
punt.
4.3. Circumcentre
El circumcentre (O) és el punt
d’intersecció de les tres mediatrius d’un triangle, que són les línies
perpendiculars a cada costat que el tallen pel punt
mitjà. Té les següents propietats:
- Està situat a
l’interior del
triangle quan aquest és acutangle; a l’exterior, quan és obtusangle; i
al punt
mitjà de la hipotenusa, quan el triangle és rectangle.
- És el centre de la circumferència circumscrita al
triangle, ja
que les mediatrius són els llocs geomètrics equidistants a dos vèrtexs,
i el punt on se'n tallen dues és equidistant als tres vèrtexs;
la distància entre el circumcentre i cada un dels vèrtexs és el
circumradi (R).
Atès que la tercera mediatriu també ha de ser
equidistant
a dos dels vèrtexs, puc demostrar que aquesta concorre en el mateix
punt,
el circumcentre.
4.4. Ortocentre
L’ortocentre (H) és el punt
d’intersecció de les tres altures d’un triangle, que són les línies
perpendiculars a cada costat que passen pel vèrtex oposat. Té les
següents propietats:
- Està
situat a
l’interior del triangle quan aquest és acutangle; a l’exterior, quan és
obtusangle; i al vèrtex on hi ha l’angle recte, quan el triangle és
rectangle.
- Si es consideren 4 punts que són els vèrtexs d'un
triangle i el seu ortocentre, llavors qualsevol triangle amb vèrtexs en
tres d'aquests quatre punts té per ortocentre el punt restant.
Demostració de la concurrència
de les altures:
A la pàgina 8 del llibre Geometria
de Sebastià Xambó (vegeu la bibliografia) apareix una construcció
geomètrica. Donat un triangle ABC, es consideren les rectes paral·leles
a cada un dels costats que passen pel seu vèrtex oposat. Prenent els
tres punts d'intersecció entre aquestes rectes es forma un nou triangle
DEF. S'observa com les altures del triangle original ABC (marcades en color verd) coincideixen amb les mediatrius del nou triangle
DEF. I per aquesta mateixa observació, l'ortocentre H d'ABC coincideix
amb el circumcentre O de DEF.
Per afirmar que les altures originals
d'ABC són les mediatrius de DEF he de demostrar que compleixen la
definició de mediatriu: primer, ser perpendiculars als costats d, e i f ;
segon, passar
pel punt mitjà d'aquests costats. La primera condició es compleix,
perquè els costats dels dos triangles són paral·lels i per tant una
perpendicular ho és a tots dos. La segona condició es complirà si AE =
AF, BD = BF i CD = CE. I si els triangles perifèrics ABF, BCD i CAE són
iguals entre ells mateixos, els segments corresponents també ho seran.
Com que una recta secant a dues de paral·leles les talla amb el mateix
angle, es pot deduir l'equivalència entre els angles interns d'ABC i
dos dels angles interns dels triangles perifèrics ABF, BCD i CAE (per exemple,
els costats paral·lels c
i f queden
tallats pel costat b,
que fa de secant, i per tant l'angle 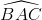 és igual a l'angle
és igual a l'angle 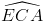 ). El tercer angle s'obté per la equació del sumatori d'angles. S'haurà
demostrat que els tres angles interns d'ABC són els mateixos que els
angles interns dels triangles perifèrics. Si es té en compte que també
hi comparteixen un costat (a,
b o c),
que és l'oposat a un mateix angle, llavors les mesures de tots
els
costats oposats a un mateix angle seran iguals entre cada un dels
triangles perifèrics i el triangle ABC; i per tant, iguals entre tots
aquests triangles. Així demostro que AE
=
AF, BD = BF i CD = CE, de manera que es
compleix
la segona condició.
Queda demostrada la coincidència entre les altures d'un triangle i les
mediatrius de l'altre.
). El tercer angle s'obté per la equació del sumatori d'angles. S'haurà
demostrat que els tres angles interns d'ABC són els mateixos que els
angles interns dels triangles perifèrics. Si es té en compte que també
hi comparteixen un costat (a,
b o c),
que és l'oposat a un mateix angle, llavors les mesures de tots
els
costats oposats a un mateix angle seran iguals entre cada un dels
triangles perifèrics i el triangle ABC; i per tant, iguals entre tots
aquests triangles. Així demostro que AE
=
AF, BD = BF i CD = CE, de manera que es
compleix
la segona condició.
Queda demostrada la coincidència entre les altures d'un triangle i les
mediatrius de l'altre.
I com a corol·lari important: com que ja s'ha
demostrat que les mediatrius
són concurrents en un punt, llavors les altures també ho seran.
4.5. Recta d’Euler
El 1765, Leonhard Euler va demostrar
que el baricentre, el circumcentre i l’ortocentre d’un triangle
pertanyen a una
mateixa recta, que posteriorment s’ha anomenat recta d’Euler (e). Té les següents propietats:
- La distància de
separació entre el baricentre i l’ortocentre és el doble que la que
separa el
baricentre del circumcentre.
- Quan el triangle és
isòsceles, l’incentre
també
pertany a la recta d’Euler.
- La recta
d'Euler queda reduïda a un punt quan el triangle és
equilàter, ja que tots aquests centres coincideixen i no es pot definir
una recta.
Demostració:
A continuació exposo una demostració geomètrica de l'existència de la recta d'Euler i
de la primera
propietat mencionada, obtinguda del web de Carlos Fleitas (vegeu
bibliografia). La idea és considerar la recta definida pel segment GO (del baricentre
al circumcentre) i intentar mostrar que l'ortocentre H també hi
pertany.
Sigui Mc el punt mitjà del costat c. Observem que el
segment McO pertany a la mediatriu de c, i per tant és
perpendicular al costat c.
Formem el triangle GMcO.
Hi realitzem una simetria central i una homotècia
de raó 2 amb centre al baricentre G per
obtenir un nou triangle, que serà semblant a l'anterior. El segment GMc' (el corresponent al nou triangle) comparat amb GMc serà el doble de llarg, estarà en la mateixa
recta, la mitjana, i se situarà a partir del baricentre cap al vèrtex. Així que,
tenint en compte la col·locació del
baricentre
respecte la mitjana, el vèrtex Mc' del nou triangle coincidirà amb el vèrtex C. Quant a l'altre
nou punt obtingut, que podem anomenar O', se situarà
sobre
la recta definida per GO,
i el segment O'G
serà el doble de llarg que el GO. En aquest moment, és important adonar-se
que, com que una homotècia manté els angles iguals, els
segments McO i O'C són
paral·lels i mantenen la perpendicularitat amb el costat c. La recta
formada per O'C,
com que és perpendicular a c
i passa pel vèrtex C, és una altura del triangle, a la
qual ha
de pertànyer l'ortocentre.
A partir del costat a del triangle,
utilitzant un raonament equivalent,
obtenim la conclusió que el segment O'A defineix
una altura del triangle, que ha de ser diferent de l'anterior
perquè A i
C són
vèrtexs
diferents. Les altures es tallen en el punt O', que és, doncs,
l'ortocentre del triangle (O'=H),
pertany a la recta d'Euler i està al doble de distància respecte el
baricentre que el circumcentre, pel costat oposat a aquest.
4.6. Relació entre l’angle intern i
l’angle central
En un triangle ABC intentem
determinar si existeix una relació directa entre els valors de l’angle
intern α
(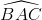 ) i de l’angle central
ε (
) i de l’angle central
ε (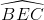 ), on E és un dels
quatre centres històrics.
Per això busquem una funció f(α) = ε.
), on E és un dels
quatre centres històrics.
Per això busquem una funció f(α) = ε.
Al baricentre: quan el punt
central és el baricentre f(α) = ε no existeix.
Demostració:
Ho demostro
mitjançant el
contraexemple: mantenint l’amplitud de α i fent variar les longituds
dels costats b
o c
s’obtenen diferents valors per l’angle
central, fet
que
implicaria l’existència de més d’una imatge diferent per un sol valor
de la
funció, que es contradiu amb la pròpia definició de funció.
A l'incentre: quan el punt
central és l’incentre f(α) = (α + π) / 2 .
Demostració:
El professor Roger Sempere
(de l'IES
Secretari Coloma) va donar-me la idea de la següent
demostració: es
plantegen
les
equacions del sumatori d’angles d’un triangle per al triangle ABC [1] i
per al
triangle BIC [2]. En aquest últim cas, s’utilitzen els angles β
/ 2 i γ
/ 2, ja que
l’incentre és allà on es creuen les bisectrius, que divideixen l’angle
en dues
parts iguals.
[1]:
α
+ β + γ = π
[2]:
β
/ 2 + γ / 2 + ε = π
[1]:
β
+ γ = π - α
[2]:
(β
+ γ) / 2 + ε = π
Substituint
[1] a [2]: (π
- α) / 2 + ε = π
π / 2 - α / 2 +
ε = π
I
aïllant
ε:
ε = α / 2 + π / 2 = (α
+ π) / 2 = f(α)
Al circumcentre: quan el
punt central és el circumcentre f(α) = 2α .
Demostració:
Ho demostro dividint el
triangle en què treballem en d’altres més petits. S’utilitza el segment
AO, que
separa l’angle α en dues parts, podem dir [1] α = α 1
+ α 2
, per formar els triangles ABO i ACO. Com que el circumcentre està
situat a les
mediatrius dels costats, és equidistant als vèrtexs (AO, BO i CO són
iguals), i
per tant els triangles ABO i ACO són isòsceles. Això implica que els
angles α
1 i α 2 tindran el mateix valor que
els angles que hi estan
situats simètricament respecte la mediatriu (com a eix de simetria)
dels costats
c i b,
respectivament. Anomenem ε1 i ε2
els dos
angles restants. Ara ja tenim prou informació per plantejar les
equacions de
suma d’angles:
[2]:
2 α1 + ε1 = π
[3]:
2 α2 + ε2 = π
I sumant-les:
2(α1
+ α2) + ε1+ ε2
= 2π
Substitució utilitzant [1]:
2α + ε1+ ε2
= 2π
Aïllant 2α :
2α = 2π - ε1- ε2
Si el situem en el punt O, correspon
justament a l’angle que buscàvem ε:
ε = 2π - ε1-
ε2 .
I igualant-ho amb l'anterior:
ε = 2α = f(α)
A l'ortocentre: quan el punt
central és l’ortocentre f(α) = π – α .
Demostració:
Començo la demostració tenint en
compte que l’angle ε que busquem queda
definit per
les dues altures, ja que aquestes passen per l’ortocentre i pels
vèrtexs B i C.
Així doncs, com que es tallen, l’angle oposat a ε (ε’), definit pels
segments
de les altures que van de l’ortocentre fins als peus d’aquestes altures
tindrà
el mateix valor que ε: ε = ε’. Ara podem fer la demostració plantejant
les
equacions de suma d’angles dels dos triangles rectangles que formen el
vèrtex
A, l’ortocentre H i els peus de les dues altures (Pb
i Pc). α i
ε’ ara queden dividits
en dues parts, podem
dir α = α 1 + α 2
i ε’ =
ε’1 + ε’2
, però en sumar les equacions quedaran igual:
[1]:
α 1 + ε’1 +
π/2 = π
[2]:
α 2 + ε’2 +
π /2 =
π
Sumant [1] i [2] (que és com
utilitzar el fet que els angles d’un quadrilàter sumen 2π radiants)
obtenim:
α + ε’ + π = 2π
I aïllant ε’ i substituint-la per ε:
ε = π – α = f(α)
4.7. Punts de tangència amb la circumferència
inscrita
En el context
de les classes
de preparació per la Olimpíada Matemàtica del 2009 a la UPC,
els alumnes vam resoldre el següent problema: "Donats els 3 costats
d'un triangle ABC, determina a quina distància s'hi
situen els punts de tangència d'aquests costats amb la
circumferència inscrita".
Resolució:
Sabem que
donada una circumferència i un punt exterior a aquesta, hi ha
dues rectes que passen per aquest punt i són tangents a la
circumferència. Per simetria respecte a la recta que passa pel punt
exterior i pel centre de la circumferència, els segments que van des
del punt de
tangència fins el punt exterior tenen la mateixa llargada. Aquesta és
justament la mateixa situació que ocorre entre el vèrtex del
triangle i la circumferència inscrita, com es representa a continuació:
Els
dos segments que, en cada costat, van dels vèrtexs al punt de
tangència han de sumar el valor del costat. Per aquesta raó,
podem
plantejar amb els tres costats un sistema de tres equacions:
[1]:
a = y + z
[2]:
b = x + z
[3]:
c = x
+ y
Utilitzant el
semiperímetre (p)
del triangle, p =
(a + b + c)/2 , les solucions del sistema
queden més senzilles. Són:
x
= p - a
, y = p - b
i z =
p - c .
4.8. Càlcul de l'inradi i el circumradi
Existeixen unes fórmules que permeten trobar el
valor de l'inradi (el radi de la circumferència inscrita) i el
circumradi (el radi de la circumferència circumscrita) a partir del
valor dels costats d'un triangle.
La longitud de l'inradi (r) és igual
a l'àrea dividida entre el semiperímetre: r = A / p . L'àrea
vindria donada per la fórmula d'Heró i el semiperímetre és la meitat de
la suma dels tres costats.
Demostració:
(Basada en el principi de la pàgina «Trilinear Coordinates» de Wolfram MathWorld, vegeu la bibliografia)
Sigui un triangle ABC, amb incentre I. Considerem els
triangles ABI,
BCI i CAI. Com que I està dins d'ABC, l'àrea d'ABC és igual a la
suma de les àrees d'ABI,
BCI i CAI:
A = A1 + A2 + A3
A1, A2 i A3 es poden expressar amb la primera fórmula de
l'àrea del triangle ( A
= bh/2 ), ja que coneixem les seves bases (a, b i c) i la seva altura
(r). Així
doncs:
A = ar/2 + br/2 +
cr/2
A = r (a + b + c)/2
A = r p
r = A / p
Que és allò que volíem demostrar.
La penúltima expressió, A = r p , també pot
ser útil per calcular l'àrea a partir de l'inradi.
La longitud del circumradi (R) és igual a una
quarta part del producte dels tres costats dividit entre
l'àrea: R = abc/(4A).
La demostració d'aquesta fórmula utilitza
propietats trigonomètriques que no s'han tractat en aquest treball, i
per això no s'inclou, però igualment es pot comprovar. És remarcable,
una altra vegada, que aïllant l'àrea en la mateixa expressió, A =
abc/(4R) , s'obté una fórmula que pot resultar
útil pel càlcul de l'àrea.
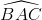 és igual a l'angle
és igual a l'angle 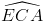 ). El tercer angle s'obté per la equació del sumatori d'angles. S'haurà
demostrat que els tres angles interns d'ABC són els mateixos que els
angles interns dels triangles perifèrics. Si es té en compte que també
hi comparteixen un costat (a,
b o c),
que és l'oposat a un mateix angle, llavors les mesures de tots
els
costats oposats a un mateix angle seran iguals entre cada un dels
triangles perifèrics i el triangle ABC; i per tant, iguals entre tots
aquests triangles. Així demostro que AE
=
AF, BD = BF i CD = CE, de manera que es
compleix
la segona condició.
Queda demostrada la coincidència entre les altures d'un triangle i les
mediatrius de l'altre.
). El tercer angle s'obté per la equació del sumatori d'angles. S'haurà
demostrat que els tres angles interns d'ABC són els mateixos que els
angles interns dels triangles perifèrics. Si es té en compte que també
hi comparteixen un costat (a,
b o c),
que és l'oposat a un mateix angle, llavors les mesures de tots
els
costats oposats a un mateix angle seran iguals entre cada un dels
triangles perifèrics i el triangle ABC; i per tant, iguals entre tots
aquests triangles. Així demostro que AE
=
AF, BD = BF i CD = CE, de manera que es
compleix
la segona condició.
Queda demostrada la coincidència entre les altures d'un triangle i les
mediatrius de l'altre.