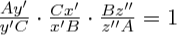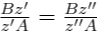5. Cevianes i teoremes relacionats
Una ceviana
és un segment del triangle que va des d'un vèrtex fins a un punt
qualsevol del costat oposat o la seva prolongació. Per analogia, el mot
ceviana també fa referència a la recta que conté el segment, que a
vegades també és anomenada
transversal
angular del triangle.
El nom ceviana
fou introduït per M.A. Poulain, en
honor del matemàtic Giovanni Ceva, que el 1678 havia formulat un
teorema que porta el seu nom i l'havia exposat en l'article De
lineis
rectis se invicem secantibus statica constructio (vegeu 5.3.
Teorema de Ceva).
5.1. Teorema de Stewart
El teorema de Stewart deu el seu nom al matemàtic
escocès Matthew Stewart; es creu que va ser ell la
primera persona
que el va enunciar, l'any 1746. Tanmateix, sembla que ja fou
descobert per Arquimedes de Siracusa en el segle III a. C. De totes
maneres, la primera demostració matemàtica de la qual es té coneixement
és la de Robert Simson, de l'any 1751.
El teorema de Stewart estableix la
relació entre
la longitud dels costats d'un triangle i la longitud d'una ceviana que
interseca amb el costat en un punt conegut. Afirma que si tenim un
triangle ABC,
una ceviana que va des del vèrtex A
fins a un punt al
costat a
que parteix el costat en dos segments m (amb un vèrtex a
B) i n
(amb un vèrtex a C),
llavors:
Ara
bé, cal
tenir en compte que perquè es compleixi la igualtat
anterior es permet que les longituds dels segments prenguin valors
negatius. La longitud d'un segment prendrà valor negatiu en cas que
aquest segment no se superposi més que per un punt amb el costat del
triangle, és a dir, quan només comparteixin el vèrtex. En canvi,
prendrà valor positiu sempre que el segment se superposi amb el costat
del triangle per més d'un punt. Per aquesta raó, es pot dir que
apareixerà un segment amb valor negatiu quan la ceviana intersequi la
prolongació d'un costat. A la pràctica, he utilitzat un
coeficient kn
que es multiplica davant de la longitud de cada segment, i que pren
els valors 1
o -1
segons la posició del segment.
En la següent representació es pot comprovar com
es compleix la igualtat per a qualsevol triangle i qualsevol ceviana:
Demostració:
(Obtinguda de Wikipedia, «Stewart's
Theorem» ,
i verificada).
Es traça una altura h del
triangle des del mateix vèrtex d'on surt la ceviana. Sense pèrdua de
generalitat, assumim que el peu de l'altura cau sobre el costat de la
ceviana anomenat m,
tal com s'il·lustra:
Amb el teorema de Pitàgores s'obtenen les
equacions:
(m - z)²
+ h² = c²
i
(n+z)² + h² = b²
Desenvolupant les identitats notables:
m² - 2mz + z² + h² = c²
i
n² + 2nz + z² + h² = b²
Multiplicant l'equació de l'esquerra per n i la de la dreta
per m:
nm² - 2mnz + nz² + nh² = nc²
i
mn² + 2mnz + mz² + mh² = mb²
Sumant les dues equacions:
m²n + n²m + 2mnz - 2mnz + nz² + mz² + nh² + mh² = nc² + mb²
Per àlgebra:
(m + n)mn
+ (m + n)(x² + h²) = c²n + b²m
Substituint a
= m + n, x² + h² = d², i per àlgebra:
amn + ad² = c²n + b²m
b²m + c²n = a(d² + mn)
I aquesta última ja és l'expressió que buscàvem.
5.2. Teorema de Menelau
Menelau
d'Alexandria (~70 - ~130 dC) va ser un matemàtic i astrònom grec del
segle I. En aquella època, l'astronomia era una ciència de cabdal
importància utilitzada, entre d'altres propòsits, per mesurar el pas
del temps. És per aquest motiu que els teoremes que conté el llibre de
Menelau titulat Les
Esfèriques
no són teoremes de geometria euclidiana, sinó de
geometria esfèrica, que és aquella que es pot aplicar a
l'esfera
celeste. L'obra conté entre 63 i 91 teoremes (segons com s'agrupin les
proposicions) que sembla que refacin Els Elements
d'Euclides per a la geometria esfèrica, tot i que
s'utilitzen mètodes de demostració diferents.
A Les Esfèriques
hi figurava la versió esfèrica del teorema de Menelau. La demostració
utilitzava cinc proposicions, que donava per conegudes. Una d'elles
era la versió plana (de geometria euclidiana) del teorema, que és la
que s'explica a continuació. Tot i així, aquest
llibre
es perdé i la demostració es difongué posteriorment a través de
l'Almagest
de Claudi Ptolemeu, que sí que contenia les demostracions de totes les
proposicions.
El teorema
de Menelau estableix la condició suficient i necessària per a
que tres punts diferents situats a cada un dels costats d'un triangle,
o a les prolongacions d'aquests, estiguin alineats. Donat un triangle
amb vèrtexs A,
B i C, i donats els
punts D, E i F que pertanyen a
les rectes dels costats BC,
AC i AB, respectivament,
llavors el teorema de Menelau estableix que D, E i F estan alineats si
i només si es compleix la següent relació:
on AF, per exemple, representa la longitud del segment que va des del
punt A fins al punt F.
Cal tenir en compte que en la igualtat anterior es permet que la
longitud dels segments prengui valors negatius, amb el mateix criteri
que en el teorema de Stewart (secció
5.1.). El
teorema es pot comprovar en la següent representació, on s'ha forçat el
punt D
a estar alineat amb E
i F.
Demostració:
(Basada
en la
de Ricard Peiró i Estruch. «El
triangle»
pàg. 49, vegeu bibliografia).
En primer lloc, cal
demostrar que el signe de la
part esquerra de l'equació sempre serà
negatiu. Anomenem f la recta que passa pels punts D, E i F, i observem que f pot no intersecar-se
amb cap costat del triangle o bé fer-ho exactament amb dos. En
conseqüència, hi haurà un nombre senar de talls amb les prolongacions
i, per tant, un nombre senar de segments amb una longitud amb valor
negatiu. Per les
propietats de la multiplicació, una quantitat senar de nombres negatius
multiplicant-se amb qualsevol quantitat de nombres positius dóna sempre
com a resultat un nombre negatiu.
⇒ En segon lloc, cal
demostrar amb valors absoluts que si els tres
punts estan alineats, l'equació es compleix. Prenent la recta f que hem definit abans, escollim els punts L, M i N que hi pertanyen tals què els segments BL, AM i CN siguin perpendiculars a f i, per tant, paral·lels entre ells, tal com s'ha representat:
Aplicant el teorema de
Tales:
 ,
,
 ,
,
I multiplicant aquestes
equacions:
⇐ En darrer lloc, cal
demostrar que si l'equació es compleix, els tres
punts estaran alineats. Suposem que l'equació es compleix. Considerem
la recta definida pels punts D i E, anomenem-la s. Aquesta recta talla el costat
AB, o la seva prolongació, en un punt G. I, com ja hem demostrat, es
compleix l'equació:
Igualant-la amb
l'equació original:
Els punts F i G pertanyen a AB, o la seva prolongació, i s'hi
situen amb una mateixa relació de distàncies respecte a A i a B, i per tant, coincideixen. En
conseqüència, D, E i F estan alineats.
5.3. Teorema de Ceva
El
teorema de Ceva estableix que tres
cevianes
de costats diferents d'un mateix triangle són concurrents en un punt P
si i només si es compleix la següent equació:
on x',
y' i z' són els punts
d'intersecció de les cevianes amb el costat. En la
següent il·lustració es pot veure com
per a qualsevol triangle, si forcem les tres cevianes a concórrer en un
punt P,
la fórmula del teorema de Ceva sempre és igual a 1:
Com hem dit abans, aquest
teorema deu el seu
nom a Giovanni Ceva que el demostrà el 1678. Tot i així, ja
havia estat demostrat al segle XI per Yusuf ibn
Ahmed al-Mutaman, un emir àrab de Saraqusta (Saragossa). El teorema de
Ceva és el teorema dual del teorema de Menelau, i precisament una de
les demostracions més
senzilles del teorema de Ceva utilitza el de Menelau.
Demostració:
(Basada
en
la d'Antonio Gutierrez, «Ceva's
theorem» ,
vegeu bibliografia).
⇒ Primer, s'ha de demostrar que donat el triangle ABC anterior, amb
el punt P
on conflueixen les cevianes i els seus peus x', y' i z', es compleix la fórmula de Ceva. Considerem el
triangle ACz'.
B, P i y' estan alineats i pertanyen a cadascun dels costats (o
prolongacions) de ACz'. Aplicant el teorema de Menelau es compleix:
Considerem ara el triangle CBz'. A, P i x' pertanyen als seus costats
(o les prolongacions d'aquests). Aplicant el teorema de Menelau de la
mateixa manera que abans queda:
Després de multiplicar les dues equacions, fer la inversa i
ordenar l'expressió s'obté:
que és la fórmula del teorema de Ceva.
⇐ Demostració que les cevianes d'un triangle concorren quan es compleix:
Considerem el punt de tall de les cevianes Ax' i By' i l'anomenem P. Allarguem la ceviana CP fins que s'intersequi amb el costat c definint un punt que anomenem z''. Ara s'ha de demostrar que z' és igual a z'' per a mostrar que les cevianes són concurrents.
Utilitzant la part d'anada (⇒) que ja hem demostrat, obtenim:
Podem igualar-la amb la primera equació donada, i simplificant obtenim:
I
com que l'expressió anterior vol dir que les posicions de z' i de z''
sobre el costat AB són proporcionals, llavors han de ser el mateix
punt. Per tant, les cevianes són concurrents, que és allò que es volia
demostrar.
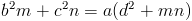
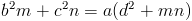
 ,
,
 ,
,