2. Introducció al triangle
2.1. Etimologia
La
paraula triangle o d'altres paraules amb forma
similar són les utilitzades en la major part de les llengües
indoeuropees per a
referir-se al concepte que estudia aquest treball. El mot procedeix del
francès
antic triangle (s. XIII), i aquest del llatí triangulum,
de
l'adjectiu triangulus: tri-
"tres" + angulus
"cantonada, angle".
És
curiós comparar aquesta etimologia amb la de quadrilàter
(del llatí quadrilaterus: quadri-
"quatre" + latus
"costat"), que per un concepte anàleg es refereix als costats en
comptes de als angles. Podria ser que aquest ús sigui herència de la
importància que tenen les relacions entre els costats en la
classificació dels
quadrilàters (paral·lelograms, trapezis), mentre que en l'estudi dels
triangles
prenen més importància els valors dels seus angles (agut, recte o
obtús).
D'altra banda, la etimologia de triangle també és
diferent de la de pentàgon,
hexàgon, heptàgon, polígon,
o la resta de n-gons,
que tenen l'origen en el grec antic gonia "angle".
Per
referir-se al triangle, els grecs sí que utilitzaven una de les seves
formes
genuïnes (com trigonon), però la singularitat
d'aquest polígon i del
quadrilàter ha fet que aquestes paraules evolucionessin de manera
diferent. De
totes formes, en català, juntament amb la paraula triangle,
d'arrel
llatina, utilitzem la paraula trigonometria,
d'arrel grega.
2.2. Definicions
En
el lèxic comú, un triangle és una “figura formada en unir tres punts no
alineats amb tres segments de línia recta”. La idea matemàtica de
triangle és tanmateix una figura abstracta, és producte de la raó i es
pot definir a partir d’axiomes.
En
el camp de la geometria, s’han anat succeint diverses definicions cada
vegada més rigoroses i formals. El primer en donar-ne una va ser
Euclides d’Alexandria, que en el primer volum de la seva obra Els
Elements, definició 19, escriu:
- “Figures
rectilínies són aquelles que estan formades per línies rectes.
Trilàters les formades per tres, quadrilàters les formades per quatre i
multilàters les formades per més de quatre línies rectes.”
Aquesta definició es completa amb les definicions
anteriors que fa de recta, línia i punt.
El
sistema axiomàtic de geometria definit per Euclides inclou un postulat,
el cinquè, que es pot formular com que per un punt exterior a una recta
hi passa una sola recta paral·lela a la primera. Aquesta és la base de
l’anomenada geometria euclidiana, que dóna lloc a les figures planes, i
a partir d’aquest tipus de geometria es desenvolupa aquest treball. Es
tracta, per tant, el concepte de triangle pla. Altres definicions
anàlogues s’han aportat per a geometries no euclidianes, com l’esfèrica
o la hiperbòlica, però no les tindrem en compte en aquest estudi.
Actualment, una definició general acceptada de triangle podria
ser:
- “Un triangle és una figura plana, tancada i amb
tres costats”.
Tot
i així, segons el context, la mateixa paraula també es pot per referir a les
rectes que formen la figura o bé a la superfície que cobreix.
2.3. Convencions d'escriptura
En
aquest treball s'aplicaran les convencions d'escriptura generals de la
geometria, sense extremar-ne la dificultat, per tal que pugui ser entès
per qualsevol persona que hagi rebut una formació en
matemàtiques
de nivell d'ESO.
Els punts importants d'una construcció geomètrica reben per nom alguna
lletra majúscula de l'alfabet llatí (P). Per punts
correlacionats, s'utilitzen lletres consecutives en l'alfabet (P, Q, R),
i per punts que comparteixen un gran nombre de
característiques
pot utilitzar-se la mateixa lletra amb diferents subíndexs (P1, P2).
Els segments s'anomenen pels punts dels seus dos extrems (PQ) i les rectes
s'escriuen amb una lletra minúscula (r). Els angles es
poden anomenar amb una lletra grega minúscula (α) o bé amb el nom dels
tres punts que el formen sota d'un barret (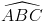 );
en aquest segon cas, el punt que s'escriu al mig és el punt on es
tallen les dues rectes que formen l'angle.
);
en aquest segon cas, el punt que s'escriu al mig és el punt on es
tallen les dues rectes que formen l'angle.
Un triangle rep el nom dels seus tres vèrtexs (ABC),
ordenats en el sentit contrari del de les agulles del rellotge, com
es fa en la resta dels polígons. Els tres vèrtexs d'un triangle solen
anomenar-se A, B i
C; i els
angles interns corresponents, α, β i γ. Finalment,
les rectes que contenen els costats del triangle reben la mateixa
lletra que el vèrtex oposat, però minúscula (a, b i c).
2.4. Propietats elementals
El
triangle és, d'entre tots els polígons amb superfície, el més simple:
és el que té menys vèrtexs i menys costats. No se'n poden modificar els angles sense modificar
els costats, i viceversa. També és l'únic que no té
diagonals. La resta de polígons es poden dividir en un nombre
finit de
triangles, mitjançant un procés que anomenem triangulació.
Això és útil per calcular àrees i distàncies d'altres figures
geomètriques que no tenen fórmules específiques per a fer-ho. A
continuació es presenten les propietats elementals més representatives
del triangle.
En
general, la concavitat es dóna quan alguna diagonal passa per
l'exterior de l'àrea que cobreix un polígon. El triangle, en no tenir
diagonals, té la propietat de ser sempre convex.
La
propietat de la desigualtat
triangular afirma que, per a tot triangle,
la longitud d'un dels costats mai no pot superar la suma de les
longituds dels altres dos: a
< b + c ; b < a + c ; c < a + b.
La suma dels angles
interns d'un triangle és igual a dos angles rectes, és a dir:
180
graus, 2π radiants o un angle pla. Una construcció que demostra aquest
fet, apareguda originalment a Els
Elements
d'Euclides, consisteix a fer una paral·lela a un costat que passi pel
vèrtex oposat. Llavors, coneixent que una secant que talla dues rectes
paral·leles ho fa amb el mateix angle, es pot deduir que els tres
angles que queden sumant-ne un de pla en aquest vèrtex són precisament α, β i γ, els angles interns del triangle.
L'àrea del triangle
es pot calcular a partir de diferents fórmules. La més coneguda diu que
l'àrea és igual a la meitat de la base (b) per l'altura (h): A = b*h / 2.
En la imatge següent es mostra com a partir d'un triangle, multiplicant
per dos la seva àrea, es pot construir un rectangle. Com que l'àrea del
rectangle és igual a la base per l'altura, i l'àrea del triangle ha de
ser la meitat de la del rectangle, llavors l'àrea del triangle és
igual a la meitat de la base per l'altura.
Altres maneres de calcular l'àrea s'expliquen als apartats 3.2.6. Fórmula d'Heró i 4.8. Càlcul de l'inradi i el circumradi.
2.5. Classificació
Els
triangles es poden classificar segons els costats o segons els
angles en tres tipus diferents en cada cas.
Segons la mesura dels costats:
- Equilàters,
si les longituds de tots els costats són iguals. En aquest cas, els
angles interns també són iguals entre ells i per tant tenen un valor
d'un terç d'angle pla cadascun.
- Isòsceles,
si les longituds de dos costats són iguals. Pot ser que el
costat desigual sigui més gran o més petit que els altres dos.
- Escalens,
si totes tres longituds dels costats són diferents entre
elles.
Segons la mesura dels angles interns:
- Acutangles,
si tots els seus angles són aguts.
- Rectangles,
si un dels angles és recte. En aquest cas, els costats contigus a
l'angle recte s'anomenen catets
i el costat oposat s'anomena hipotenusa.
- Obtusangles,
si un dels angles és obtús.
Donat que la suma dels angles és igual a un angle
pla, no hi pot haver més d'un angle recte o obtús en un triangle.
2.6. Criteris d'isometria i de semblança
Es diu que un triangle és isomètric
a un altre quan les mesures dels costats del primer són les mateixes
que les del segon. En general, una figura és isomètrica a una
altra si per passar d'una a l'altra és suficient amb utilitzar
transformacions que mantenen les mesures dels costats, com la
translació, la rotació o la simetria. Per tal què dos triangles siguin
isomètrics és suficient que compleixin alguna de les següents
condicions:
- Les mesures dels tres costats són les mateixes.
- Les mesures de dos angles i d'un costat són les
mateixes.
- Les mesures de dos costats i de l'angle que formen
són les mateixes.
Es diu que un triangle és semblant
a un altre quan els valors dels angles del primer són els mateixos que
els del segon. En general, una figura és semblant a una altra si per
passar d'una a l'altra és suficient amb utilitzar transformacions que
mantenen els valors dels angles, com la translació, la rotació, la
simetria o l'homotècia. Per tal què dos triangles siguin semblants és
suficient que compleixin algun dels criteris d'isometria o bé alguna de
les següents condicions:
- Les mesures de dos angles són les
mateixes.
- Les mesures dels costats són proporcionals.
- La mesura d'un angle és la mateixa i les dels dos
costats que el formen són proporcionals.
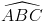 );
en aquest segon cas, el punt que s'escriu al mig és el punt on es
tallen les dues rectes que formen l'angle.
);
en aquest segon cas, el punt que s'escriu al mig és el punt on es
tallen les dues rectes que formen l'angle.