La realització del llibre "Un all i mig: Com s'escriu? " no va ser un objectiu determinat a priori, de l'aula dels Rat-penats de 4rt, sinó que va ser fruit del gran interès mostrat per l'aula entorn a la pregunta: Com s'escriu un all i mig?

Va ser sorprenent com una qüestió que semblava que podia ser una de les reflexions puntuals que podíem fer després d'una activitat sorgida en el Taller entorn a la Festa del Carnaval, es va transformar en un debat quasi diari, que anava i venia, amb noves idees que venien a refermar les idees anteriors, a ampliar-les o a refutar-les.

Va ser enmig d'aquest debat que es va trobar interessant recollir totes les idees que anaven sorgint, i elaborar un recull. Recull que s'aniria ampliant a mesura que la història de l'all i mig s'anés desenvolupant.

El format de llibre s'escollí per tal que pogués circular per la classe i pogués ser consultat i interpretat per tots els nens i les nenes.

Va ser el moment d'explicar totes les idees, les reflexions... que havíem anant tenint.

El llibre no pretenia recollir totes les produccions dels nens i nenes de la classe, sinó que reflectís el procés que es va seguir i poder veure com anaven evolucionant les idees i els coneixements.
Calia que les idees de tots i totes s'integressin en una història que compartia tot el grup classe i que l'escrivíem entre tots, amb les idees errònies i provisionals, amb els relats que venien de casa, el meu pare, la meva mare m'ha dit,..... amb les maneres de representar de cadascú, amb els dubtes...

Taller: El Carnaval. La xatonada

En el marc de la festa del carnaval, els nens i nenes des de 3r fins a 6è celebren La Xatonada. El dia del Dijous Gras tots els nens i les nenes es queden a dinar a l'escola i mengen el típic menú del Dijous gras: xató, truites i de postres merenga.

Tos els ingredients i plats els proporciona el menjador escolar, menys la salsa del xató que l'elaboren els mateixos nens i nenes.

Abans, però, es va fer un treball de revisió de la recepta que s'utilitzà l'any anterior i s'adaptà la recepta i la quantitat d'ingredients. Una vegada celebrada la Xatonada, tocava fer una valoració de la festa.
La recepta amb els ingredients per a quatre persones fou la que es deixà com a patró per l'any vinent.

Sobre aquesta recepta es va proposar calcular els ingredients per a un altre nombre de persones.

CÀLCULS DELS INGREDIENTS PER A 8, 10 I 12 PERSONES

Partint de la recepta original del xató per a 4 persones, els vaig proposar calcular la quantitat d'ingredients per a 8, 10 i 12 persones. El treball era individual.

Tots els nens i les nenes es posaren a resoldre els càlculs. Les seves idees sobre quines eren les relacions entre els nombres i la manera que els havien d'utilitzar per poder fer els càlculs generaven textos de calcular propis de cada un d'ells.

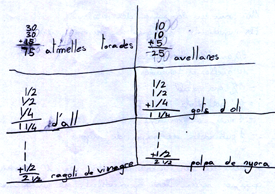
Et trobaves nens que després de diversos tempteigs havien pogut resoldre els càlculs mitjançant una taula d'equivalència. Altres que utilitzaven representacions gràfiques per resoldre el càlculs dels grans d'all. Em va agradar la manera que tenia en Pol de buscar la quantitat d'all i d'oli. Entenia que havia de sumar les quantitats, però com que ho havia de calcular per a 10 persones, la relació numèrica que havia d'establir era el doble més la meitat.
Sumava les fraccions utilitzant el mecanisme de la suma en nombres naturals, però com que coneix el significat de cada número fraccionari, és capaç de trobar el resultat.

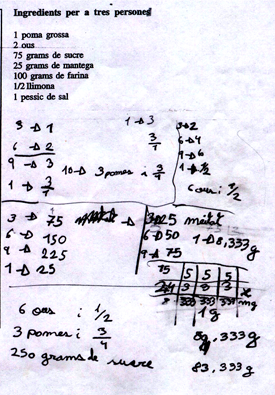
Alguns nens i nenes s'atreviren a calcular els ingredients d'un pastís de poma que la recepta especificava per a tres persones.

La Júlia utilitza taules d'equivalència per resoldre els càlculs de cada ingredient. En el càlcul de la quantitat de mantega, ha de resoldre mitjançant una divisió el càlcul dels grams de mantega per una persona. Organitza els números en una taula i reparteix primer 15 grams entre 3, després 9 més ( ja té 24 grams repartits) però li queda un gram per repartir tots 25. M'ho explica i acordem fer-ho amb la calculadora.
Després de resoldre tots aquests càlculs, d'haver observat les estratègies que utilitzaven, les dificultats que cada un tenia... s'havia de fer una devolució.

En qualsevol de les situacions que es plantegen a la classe s'obren diverses línies possibles de treball. El mestre decideix quina línia escollir. No ho fa arbitràriament, sinó que darrera de qualsevol decisió hi ha un propòsit. A vegades és una decisió pragmàtica, o a vegades es vol aprofundir en unes estratègies o en unes altres.
Una de les possibles devolucions era fer un treball de comparació de resultats i de les estratègies de càlcul utilitzades. No era la meva intenció compartir les estratègies de càlcul en aquell moment. Hi havia hagut altres situacions en què s'havia prioritzat aquesta línia de treball. La meva intenció era reflexionar sobre dues qüestions: quines eren les relacions numèriques que havíem utilitzat per fer els càlculs i compartir les diferents formes de representar els nombres fraccionaris. Ho vaig plantejar a tota la classe en forma de dues preguntes:
1. Quina és la relació que hi havia entre les 4 persones de la recepta i el número de persones per qui volíem calcular els ingredients de la recepta?
2. De quines maneres havíem escrit la quantitat d'all que necessitàvem per fer el xató per a 8, 10 i 12 persones?

La primera establí un diàleg entre tots els nens i nenes de la classe i s'arribà a la conclusió que per calcular les quantitats per a 8 persones era el doble de la recepta inicial, per a 12 era el triple, i per 10 persones, era el doble i la meitat més.

Pensava que la segona qüestió que els plantejava m'obriria una línia de treball sobre els nombres fraccionaris, i amb aquest convenciment la vaig plantejar. A la classe acostumem a recollir tots aquests debats en els llençols de manera que quedi registre de les qüestions que es debaten i dels acords que es prenen. L' escriure-ho a la pissarra no facilita el que quedi registrat.

Van anar apuntant les maneres que havien escrit mig all i després un all i mig.

Explicaven perquè ho havien escrit d'una manera o d'una altra. En general tots estaven d'acord. Seguiren el mateix procediment amb un all i mig:

Cap havia escrit 1'5. Els vaig preguntar si també podíem escriure-ho així: 1,5
La sorpresa va ser quan una gran majoria digueren que no. La pregunta la vaig fer quasi bé sense pensar, només em semblava que s'havia de completar amb un dels nombres que faltava. No em pensava que hi hagués aquests dubtes; jo vaig ser la primera sorpresa.
Va ser llavors quan va començar el debat dels nombres decimals.
Cadascú digué la seva, no es posaven d'acord amb la justificació, però tenien clar que no podia ser.
La majoria dels arguments coincidien i afirmaven que 1,5 sí que indicava un i mig, però que no servia per aplicar-ho a l'all i mig. Podien aplicar-ho a unitats de mesures, a euros, però no a objectes, perquè eren coses senceres.

Hi havia intervencions de nens i de nenes que realment intentaven convèncer els altres. Aquest intent de convenciment els feia estructurar els seus arguments i quan els altres els rebatien, els havien d'estructurar de nou.

Era el moment d'escoltar les idees que tenien, se'ls havia de donar la possibilitat d'argumentar, de justificar les seves idees.

Es va deixar penjat a la classe, el llençol de les diferents maneres d'escriure, mig all, i un all i mig, junt amb altres acords matemàtics de la classe. Aquest llençol sovint era centre de comentaris entre uns quants que discutien o comentaven el problema.

L'endemà els vaig demanar que expliquessin per escrit el que ells pensaven sobre aquesta pregunta:
ES POT ESCRIURE 1,5 ALLS PER EXPRESSAR UN ALL I MIG?

Varen elaborar textos argumentatius per justificar les seves idees respecte de la pregunta formulada. Tots van ser capaços d'explicar les seves idees, amb textos més o menys complexes, amb arguments més o menys fonamentats.

Sempre ets conscient de la diversitat de l'aula, però a vegades aquesta diversitat se't mostra d'una manera més evident i palpable. Aquesta era una ocasió per observar la riquesa de les idees dels nens i nenes i per adonar-te'n de la importància els processos comunicatius en l'aprenentatge de les matemàtiques. Hem de procurar donar veu a tots els alumnes, escoltar-los, deixar-nos seduir, i després actuar en conseqüència.

Era curiós com d'un dia per l'altre, les idees anaven evolucionant. El dia de la conversa quasi bé tots coincidien en què no era possible. En canvi l'endemà els seus arguments ja estaven plens de matisos molt subtils, que feien entreveure la part d'emoció que els va produir el debat i que aquest s'havia traslladat també a casa. Es podia deduir per la manera que van arribar l'endemà a classe: La meva mare m'ha dit que... el meu pare... jo he pensat que potser... aquests eren el tipus d'expressions que utilitzaven.

Vaig llegir-me tots els textos. Aquells textos eren demostracions i justificacions de les idees que tenien els nens i les nenes sobre els decimals i m'adonava que a l'escola s'havia de donar valor a les argumentacions. Era necessari, que davant de qualsevol afirmació matemàtica, tinguessin l'oportunitat de justificar-la amb els seus propis arguments.

Al llarg de tot el procés de l'all i mig, m'anava preguntant què passava abans quan no m'adonava del valor, ni de la importància de la comunicació a l'aula: abans deixava intervenir poc, no sabia bé què fer amb les explicacions de les criatures. Ara sóc conscient que desaprofitava una gran oportunitat d'enriquir l'aprenentatge. El valor que ara dono a la comunicació és diferent, la comunicació ens ha de servir com a instrument per comprendre i per arribar a generar estratègies de solució.
Els arguments que donaven ja no coincidien amb els del primer dia, quan va sorgir el problema. El fet de plantejar la pregunta, de parlar-ho, de comentar-ho a casa... havia propiciat l'ocasió per pensar què volia dir realment 1,5. En les seves respostes escrites es poden observar com van reelaborant les idees.

En l'exemple, en F. utilitza una negació basada en la relació de la meitat que ell suposa que hi ha d'haver entre l'1 i el 5 igual que la que existeix entre un all i mig all. Després al final incorpora un dubte i pot ser que ho hagi sentit a algun company o companya.

En moltes escoles un fet com aquest de suposar que ho havia vist o sentit d'algú i ho hagués copiat és motiu ja de fer les activitats sols i aïllats sense cap possible contacte amb els altres nens i nenes.

La valoració que en faig no és aquesta. Aquest nen incorpora la idea d'un altre company però no esborra la seva, sinó que l'expressa entre parèntesis, com si estigués dient: Dubto de l'afirmació que estic fent però no estic segur ni d'una ni de l'altra.
Hem de procurar que els nens i les nenes sàpiguen que poden aprendre dels altres i amb els altres i els mestres treballar per aconseguir-ho. Com he dit abans la comunicació ha de ser un valor de l'aula, la comunicació com element essencial en qualsevol procés d'aprenentatge. Aquesta comunicació no s'ha de limitar només a les converses entre els companys o amb el mestre, sinó que s'han d'establir discussions de grups per clarificar, qüestionar, argumentar. S'haurien de crear i promoure situacions on els nens i les nenes conversessin procurant argumentar les seves idees per convèncer els altres. No conversar per conversar, sinó procurant donar sentit a les idees matemàtiques i utilitzar-les per arribar a la solució dels problemes.

Aquest tipus de converses no només es donaven a l'aula, sinó que per les respostes que feien, s'intuïa que en alguns casos també s'establia un diàleg matemàtic amb la família.

Per exposar els seus arguments, aquesta nena estructura el seu text d'una manera determinada. Primer fa una afirmació que respon a la pregunta formulada, després fa servir dos arguments molt utilitzats en moltes altres justificacions. Però abans d'explicar el segon argument, es pregunta per la qüestió en què dubta, la part decimal. Ho justifica explicant que depèn del nombre de trossos que considerem.

Acaba fent una afirmació personal, com volent manifestar que està molt segura dels seus arguments.

En el cas de la segona figura, utilitza tot allò que sap sobre el valor i les equivalències de les unitats de diferents magnituds.

Sovint els mestres no sabem què fer amb els arguments i amb les idees dels nens i de les nenes. En aquest cas calia retornar al grup la responsabilitat d'interpretar els arguments que havien donat a la pregunta de si l'expressió numèrica 1,5 era vàlida per expressar un all i mig. Aquest retorn es pot fer de moltes maneres diferents.

En la devolució es presentaren totes les idees, i es va tornar a plantejar el problema a tot el grup. M'agradava veure com es qüestionaven entre ells. Era conscient que les meves intervencions no podien ser categòriques, ni tampoc de desinhibició. Havien de servir per centrar el debat, per dirigir i fer-lo evolucionar i amb ell les idees i les argumentacions sobre l'1,5.

Pensava que l'activitat no donaria més de sí després de la devolució dels seus escrits. En canvi, cada dia sortia el tema. Que si jo ho he preguntat a casa, que si el meu germà m'ha dit... Al final ja en dèiem el problema de l'all i mig.

Vaig pensar que això s'havia de recollir d'una manera o altra, tant podia ser amb un mural com en un llibre. Els càlculs dels ingredients i les idees sobre 1,5, varen omplir les primeres pàgines del llibre.

En aquest moment estàvem en un punt que el tema interessava però jo pensava que necessitàvem idees noves per poder anar més enllà. Els vaig plantejar si havien vist números com l' 1'5 en altres llocs.
Tinc la sensació que la majoria, per no dir tots, van considerar que com podia qüestionar una cosa tan evident.

D'aquí va sorgir la idea de buscar nombres amb coma, nombres decimals.

1,5 en el nostre entorn

Van anar portant números decimals que trobaven: de diaris, d'envasos, de caixes, fulls de propaganda... S'enganxaven en un full en blanc i es penjaven a la cartellera de la classe. Els vaig demanar si en estones lliures podien llegir els números i podien escriure les idees que tenien sobre aquell número que el seu company havia marcat.

Passats uns dies, quan molts dels nens i nenes havien expressat les seves idees als fulls de la cartellera, vaig recollir-ho i vaig escriure les idees en unes etiquetes i les vaig enganxar al costat del full de propaganda o del full de diari en qüestió.

La devolució la vaig organitzar en un treball per parelles. Les parelles llegien les anotacions que havien fet altres companys i companyes i escrivien els seus arguments, si estaven d'acord o no, si creien que hi faltava alguna explicació... Els arguments i contraarguments que utilitzen per explicar els nombres decimals que observen en els prospectes, etiquetes i diaris, són semblants als que feien servir per explicar el problema de l'all i mig.

Un dels textos numèrics que van portar fou una etiqueta d'una ampolla de llet. La primera argumentació que fan encara manté la idea inicial que 1'5 sí que es pot utilitzar per litres, però no per coses senceres, com és un pastís i es justifica d'aquesta manera: l'1 vol dir 1 litre i el 5 és la meitat del 10 i un pastís podria ser de 10 trossos, la meitat és 5. Però si fos de 20 trossos, la meitat seria 10 i no pot ser.

La parella que revisava va contestar: "No, perquè ens fem un lio. Perquè no s'entén. No estem d'acord amb això, perquè aquest sistema és de 10, només de 10 i, com que la meitat de 10 són 5, 1,5 sí que és 1 i mig. I que no estem d'acord amb aquest nen o nena".

El problema de l'all i mig ens porta de cap

Després de l'activitat dels nombres decimals, en tornem a parlar i tothom va dient la seva opinió. Les anem recollint en un llençol, agrupant les que coincideixen.

És sorprenent com expliquen la seva i l'argumenten i no es deixen influir per la dels altres. Després d'explicar els seus arguments, ja comencen a qüestionar afirmacions que altres han dit o a completar les seves.

Les afirmacions que feien són aquestes:

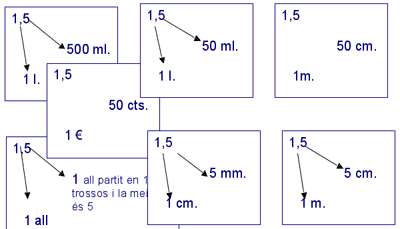
Tots els exemples que utilitzaven per argumentar-ho són en unitats de mesura d'alguna magnitud: euros, metres i centímetres, litres i mililitre. D'aquí podíem estirar un fil, tant per treballar els nombres decimals, com per estudiar les equivalències entre les unitats d'una determinada magnitud.

Però en aquell moment la qüestió que els interessava més, era comprendre l'afirmació que feia la Paula: Hi ha un sistema en què tot és 10.

Després d'aquest debat, comencen a estirar la idea de la partició de la unitat, l'all en 10 parts.

Però algú encara ho qüestiona:

Després de la conversa, queda una pregunta a l'aire: Què és això del Sistema Decimal en què tot és deu, en què tot es calcula de 10 en 10?

Per tal d'anar aclarint les coses, i ordenant les idees que constantment diuen sobre el sistema decimal, els vaig fer aquesta pregunta:

Què en penses d'aquesta idea: comptem de 10 en 10? Algunes de les seves respostes foren aquestes, en les dues pàgines del llibre de l'all aquí reproduïdes.

Les respostes que donen són diverses i les podríem ordenar en diferents categories, aquelles que es basen en la idea del comptatge de 10 en 10, basant-se en la lògica que regeix la sèrie numèrica, i les que analitzen els nombres decimals i per extensió el sistema de numeració decimal.

Alguns dels arguments expressen dubtes, són conscients que les idees que tenen sobre els decimals són provisionals, altres estan més segurs i s'aventuren a fer afirmacions.
Els nens i nenes són conscients que hi ha coses que encara no entenen, i ho expressen amb tota llibertat sense cap recança ni por, amb la confiança que ja ho aniran entenent, que ja tindran altres idees sobre el sistema de numeració decimal.

Després de totes aquestes activitats, diàlegs, reflexions, fins i tot discussions, s'havia arribat a un punt mort, que nosaltres sols no podíem tirar més endavant, que necessitàvem ajuda externa. Va ser quan va sorgir la idea de preguntar-ho a la classe de 6è.

Entre tots elaboràrem una llista de qüestions a preguntar i se'ls va donar a la classe de 6è. Ells s'ho van preparar i un dia ho van venir explicar a la classe.

Va ser molt emocionant veure l'Alejandra i en Fèlix a la classe explicant coses dels decimals als nens i nenes de 4t. Se'ls notava una mica nerviosos i també contents i emocionats.

La sessió va anar així:

EL SISTEMA DECIMAL

Aquesta va ser la conversa que vam tenir:

Júlia: Tot el problema va venir de la xatonada i de l'elaboració de la salsa del xató. La recepta era per a 4 persones. Després la vam calcular per a 8, 10 i 12 persones. Ens va sortir el problema d'un all i mig. Ho podíem escriure de diverses maneres, però ens va sortir el problema de si es podia escriure 1,5 per dir un all i mig. Ens van sortir molts problemes, entre ells què eren els nombres decimals.

Mestra: Què són els nombres decimals?

Alejandra: Són per exemple l'1 i el 2.
Entre l'1 i el 2 hi ha alguna cosa.
Dibuixa a la pissarra

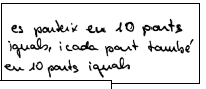
Alejandra: Tot pot ser 10, perquè tot va de 10 en 10. És un sistema que es va inventar perquè anés de 10 en 10, però pot ser que hi hagi 10 parts, 100 parts o 1000 parts.

Josep Mª: Però sempre es compta de 10 en 10.

Alejandra: Sí, sempre.

Lia: Perquè sempre és 10

Alejandra: El regle també va així:
Del 0 al 1 1 cm.
Posa com exemple l'esborrador. Compara la meitat de l'esborrador i diu que 1/2 = 0,5

Alvaro: Amb en Pol vam treballar això de l'1 i mig amb una pizza. Ell deia que eren 100 parts i 1/4 eren 25.
Jo també vaig dir que si feies 10 parts i n'agafaves 2,5 era el mateix.

Alejandra: No t'he entès molt bé.

Alvaro: Ho fèiem en una pizza rodona...(repeteix l'explicació).

Alejandra: Agafa un compàs de pissarra, dibuixa una circumferència. La vol dividir en parts iguals.
La circumferència fa 360º,...
Pregunta:
Saben fer regles de tres?

Tots se la miren amb cara d'estranyats.

Mestra: No

Alejandra: Com ho expliquem?

La circumferència fa 360º, i una circumferència és 1 ( assenyalant-la a la pissarra).

I ho escriu a la pissarra:

360º ---------- 1
----> --------- 0,4

no sabem quants graus són.
Però es fa així:

360 x 0,4 = 54
54 : 1 = 54º

Amb el semicercle marquem els 54º i es fan les divisions.
Tota la classe els mira amb cara de no entendre res, ara bé estan molt callats i expectants.

Alejandra: Això és la part del 0,4 (assenyalant i pintant la part corresponent al 0,4).

Alvaro: Però en quant es divideix, en 10 o en 100?

Alejandra: En 360º

Júlia: De tot això del 0,4, no he entès res.

Alvaro: A la carretera surt una rodona amb una rampa i hi ha el 6% de baixada. Potser vol dir que té molta baixada o poca.

Mestra: Això que dius et refereixes als graus.
Ho deixarem pendent d'estudiar.
Tornem al problema de la pizza. Si ens hem de menjar 0,4 trossos de pizza....
Si la dividíssim en 10 trossos... Ho podríem fer sense graus?

Alejandra: Divideix la pizza en 4, després en 8... després en 10 trossos. No li queden iguals.

Hauríem de calcular en graus.

Mestra: Si ens mengem 0,4, quan seria?

Alvaro: 4 parts i quedarien 6 parts. (Les assenyala a la pissarra)

Mestra: Ahir en Pol es feia una pregunta: si 1/4 d'una pizza era 0,25

Pol: Si la pizza feia 100 grams, cada 1/4 és de 25 grams.
Si era de 10 en 10 dèieu que seria 40
I jo vaig dir que jo m'imaginava de 100.

Mestra: Aquests dies dèieu que tot era 10, que el sistema decimal tot era 10.

Alejandra: Es pot multiplicar 10 per 10.
Sempre hi ha un nº que es composa de 10
10.000 ---> 1000 vegades 10

Júlia: Això que va dir en Pol, que 25 era 1/4, abans no ho entenia.
No sabíem si tot era 10.
Però ara, 1/4 és 2,5. Perquè la meitat de 5...
5 era la meitat

La meitat de 5 seria 1/4 i seria 2,5

Alejandra: Si jo parteixo la rodona en 4 parts (ho fa)...
Si la pizza és 1 això, la meitat serà 0,5
Si és 10 això, la meitat serà 5
Si és 100 això, la meitat serà 50
Si és 1000 això, la meitat serà 500
i escriu a la pissarra:
Si 1 part i assenyala la quarta part
1------>0,25 perquè és una part més petita.
10----->2,5
100---->25
... En un dibuix de la sèrie numèrica, explica la posició de l'1,5

Paula M: No sabem si 22,03m és igual que 22,3m

Alba: Quan vam construir la línia del temps, en mesurar les parets ens va donar diferent: 22,03m i 22,3m.

Alejandra: Quan els 0 estan darrera del nº, no passa res però quan es posa abans sí que importa...

Pol: Ara ho he entès. El meu pare deia que no era igual.
Perquè 22,03, entremig de la primera ratlleta encara pots fer més ratlletes.
...

Mestra: Si tenim 22,003 i 22,03, quin és el més petit?

Lia: Jo crec que és 22,03

Alejandra: És més petit el 22,003
Ho explica en la recta numèrica.

...

Mestra: No hi havia més problemes, més dubtes...

Nil: No sabíem si el 0 era un nº

Júlia: El 0 és un nº encara que no valgui res perquè sinó el 100 seria 1.

Arnau: Si el 0 no existís, el 50.000 solament seria 5

Oscar: Ens imaginem.... Dibuixa
Com ha dit la Júlia, sense el 0 no
valdrien els nº, però a vegades si.
Els nº romans per fer el cent tenien C, no posaven 100.
El 0 no existia. Quan els àrabs van inventar el 0, li van posar un altre nº i el van multiplicar perquè quedés un nº més gran.

Alvaro: Si el 0 no existís i existís de l'1 al 10, no podríem fer el cent-ú, perquè tot seria junt.

Alejandra: En veritat en el sistema decimal no és de l'1 al 10 sinó del 0 al 9.

Nil: El 0 pels romans no existia, ho hem estudiat i no el tenen.

Josep Mª: No coneixien el 0 els romans.

Júlia: Els romans no tenen el 0 perquè el 10 no en fan en dues xifres, sinó que el fan amb una X

Ainoa: Té raó, el 10 només el fan amb una xifra, si el 0 existís el farien en dues xifres però com que no existeix el fan amb una.

Pol: Si nosaltres no tinguéssim 0 potser saltaríem directament al 11 i al 12

Arnau: Si no existís el 0 comptaríem 1,2,....0,11,12....19,21,22...

Nil: Igual que s'ha inventat el 0 podríem haver inventat un altre nº.

Oscar: El 0, el 0 del mig sí que existeix, a dalt sí que existeix, a baix no existeix.

Alvaro: El 0 romà no existeix
10 X
100 C La X i la C són diferents.

Mestra: El X i el C no tenen cap relació, en canvi en el nostre sistema sí?

Alvaro: Sí perquè té 0

Mestra: Abans la Júlia ha dit que el 0 ha de tenir un valor. Fixem-nos amb el 0 i els decimals. 22,003 i el 22,03

Pol: No ens podem queixar massa dels nº romans perquè encara els utilitzem. Ens costa una mica explicar-ho. L'altre dia vam intentar explicar el nº romans i ens va costar.

Oscar: Sabem si existeixen el nº decimals en els nº romans?
...

Arnau: No ho he sentit bé.

Oscar: Sabem si existeixen el nº decimals en els nº romans?

Nil: Em sembla que sí, perquè el 10 existeix en la muneració romana.

Mestra: L'Oscar pregunta si existeixen els decimals en els nº romans?

Alejandra: Crec que no perquè si no tenen el 0 que hi ha entre l'1 i el 2, com ho fas si no tens el 0?

Alvaro: Igual com pots
10.000 deu vegades

Alejandra: No ho sabem, hauríem de buscar-ho.

Mestra: Però podríem parlar-ne a veure quines idees teniu vosaltres?

Júlia: Estic d'acord amb l'Alejandra que no existeixen, perquè, com s'escriuria el 0,4?

Josep Mª: Igual ells poden escriure l' u i mig

Mestra: Com deuen escriure l'1 i mig?

Josep Mª: L'I romà i el V

Mestra: Els romans tenien necessitat del nº decimals? Perquè els fem servir els nº decimals nosaltres?

Alvaro: Per mesurar, els litres, els centilitres...

Júlia: Per les unitats de mesura, els metres, els centímetres...

Pol: Pot servir per viure millor...

Mestra: Estàvem dient que perquè servien els nº decimals, i dèieu per mesurar, però en Pol ha dit que per viure millor...

Nil: Ho necessitem per mesurar... si no, no podríem fer cases...

Pol: Per anar a comprar

Mestra: Però creieu que els romans els necessitaven?

Alejandra: Si vols fer un pont que fa 12 per 5, potser ells no ho calculaven amb els nº sinó que ho calculaven d'una altra manera.

Alvaro: Abans quan el meu pare era petit, es mesurava per pams, llavors van descobrir els cm...

Mestra: Ens queda pendent investigar si els romans tenien nº decimals.

A partir del problema de l'all i mig van emergir nous objectes de coneixement, per exemple, el 0 i els romans. La història de l'all i mig s'acabava, i en començava una altra: potser la del 0 i els romans? o si serveixen el nombres naturals per viure millor?