Aquesta experiència és un projecte col·lectiu que s'emmarca en la unitat temporal que anomenem Taller. Sorgeix de la necessitat de l'escola per preparar una festa, en aquest cas el Nadal.
La finalitat dels tallers setmanals que es fan en el centre és la gestió de les festes. Serveixen per planificar i organitzar les festes d'una manera compartida amb famílies, barri, etc. Tots els cicles fan propostes i distribueixen les tasques a fer a la resta del centre: decoració, propagandes, actuacions...., implicant tant a professionals com a alumnat i famílies.
Un mestre coordinador fa de fil conductor que relliga en últim terme totes les propostes, aportant la visió organitzativa més general, fent d'enllaç entre els tallers dels diferents cicles.
La celebració de les festes ens ofereix l'oportunitat d'integrar-nos en el medi i poder realitzar diverses activitats: tallers de plàstica, investigació històrica, escriptura i representació de textos, dades numèriques, dissenys... treballar plenament des de la globalització.

El taller de Nadal es concreta en aquests eixos de treball:

- Calendari d'advent, cada dia, per sorteig, una classe obre una caixa d'un calendari gegant col·lectiu que hi ha penjat a l'espai central de l'escola. Allà s'hi troba un regal construït per una altra classe i especialment dedicat.

- Amic invisible, cada persona de la classe prepara i construeix un regal per a un amic invisible, previ sorteig. Se li ofereix a la persona indicada amb un poema dedicat.

- Esmorzar col·lectiu i cantada de nadales. Es fan quatre agrupaments diferents, de diferents edats, en diferents recorreguts, per tal d'oferir a la gent del poble un repertori de cançons de Nadal. L'alumnat de 6è prepara aquests recorreguts, tenint en compte les diferents edats, els llocs del poble més concorreguts i l'horari.

En aquest exemple veurem la classe de 6è dels P.G.G., Petits Grans Genis, dissenyant i construint el regal del calendari d'advent per la classe de 3r dels Espies.

Hem de fer el regal del calendari d'advent a la classe dels Espies

Durant el mes de novembre s'ha realitzat el sorteig de les classes pel regal del calendari d'advent. A la classe de 6è dels P.G.G. els ha tocat fer el regal sorpresa a la classe de 3r dels Espies. La mestra planteja la situació d'aula com un moment de comunicació, en el que cal encetar un procés de diàleg on compartir idees, arguments, opinions, dubtes... Els cal iniciar un procés d'investigació, disseny i construcció d'un producte que ha de ser potent a nivell emocional. Cal arribar al cor dels Espies.
En situació de gran grup comença la pluja d'idees sobre els seus gustos per l'edat, pel nom de la classe, pel tema del projecte... Tot plegat els porta a concretar-ho en aquestes idees:

- la mestra és la Pilar
- són vint-i-quatre, onze nens i tretze nenes
- tenen vuit i nou anys
- són la classe de 3rA
- es diuen Espies
- fan el projecte d'Egipte.

Aquests supòsits els fan pensar en uns gustos i interessos determinats:

- per l'edat encara els poden agradar els titelles
- pel tema dels projecte els poden agradar les piràmides
- pel nom de la classe els pot agradar fer com si fossin espies

Aquest és un moment difícil. Tothom aporta i té ganes de concretar, amb la immediatesa que caracteritza les persones d'aquesta edat. La mestra aprofita i condueix aquest moment de comunicació. Cal fer participar per dissenyar una proposta rica i complexa, que els faci fer un producte en el que puguin millorar el seu aprenentatge en la seva globalitat. Estan participant d'un moment comunicatiu en el que es posa de manifest que encara no saben i que caldrà escoltar-los per poder avançar i construir.

Van sorgint altres idees, d'altres tallers, d'altres cursos... es van fent connexions....
- ...els altres anys hi havia alguna llaminadura....
- ...podem fer un regal per la classe i un per cadascú...
- ...la llaminadura d'aquest any és una moneda de xocolata...
- ...tots junts són vint-i-quatre...
- ...fem una caixa amb forma de piràmide per posar les monedes i serà per decoració de la classe....
- ...no, fem un titella per cadascú, amb el cap de la seva foto i disfressat d'espia...
- ...no, fen una piràmide per cadascú...
- ...i per la classe també...
- ...fem-ho tot..
- ...com?...
- ... si fem una construcció per amagar-ho tot...
- ...posem també un enigma, que l'endevinin i ho trobin amagat a un altre lloc...
- ...la moneda dins d'una piràmide, la caixa personal de la xocolata...
- ...una pila de piràmides amb les monedes...
- ...tot dins les piràmides i tot a mida de cada cosa dels titelles, de l'enigma, de la moneda de xocolata...

...UNA PILA DE PIRÀMIDES, EN FORMA DE PIRÀMIDE I UNA CAIXA-PIRÀMIDE QUE HO CONTINGUI TOT!

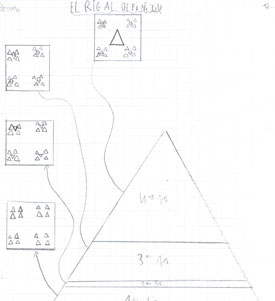
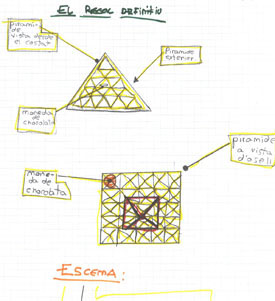
Esquema de l'alumna de 6è encarregada de recollir les idees pel regal.

Els P.G.G. dialoguen per aconseguir un bon resultat, un bon regal!

Les primeres problemàtiques

Les idees es van enllaçant les unes amb les altres. Arriba el moment de la concreció. El grup es comença a imaginar el regal.

La mestra recull les idees en el llençol "Idees pel regal". Tothom veu clar que seria interessant aconseguir una pila de vint-i-quatre piràmides apilades en forma de piràmide. S'enceta la discussió i comencen a sorgir les primeres propostes per fer la pila.

En aquest moment es posen en marxa les estratègies personals per analitzar les característiques i propietats de les figures geomètriques, de dues i tres dimensions. La situació afavoreix el desenvolupament de raonaments matemàtics sobre les relacions geomètriques.

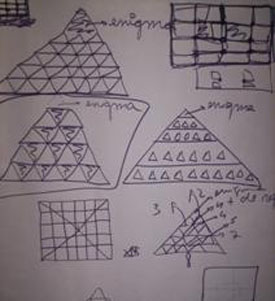
En principi, la conversa es desenvolupa imaginant la mida de la piràmide més gran. Si totes les piràmides tenen 5cm de costat a la base quadrada, ens podem imaginar una piràmide gran de 120cm de costat (veure imatge superior). Només s'han de posar totes les piràmides petites afilerades, una al costat de l'altra, i ja tindrem la pila de piràmides en forma de piràmide. Quan la mestra ho dibuixa en el llençol comencen a adonar-se que el que han fet no és una pila, és una fila. El resultat final no és una caixa en forma de piràmide, és un prisma rectangular!. La discussió que s'enceta és molt interessant: es fan connexions amb coneixements geomètrics que ja tenen. Saben que la superfície del quadrat és lxl. Per tant, si es fan fileres de vint-i-quatre piràmides sortirà una base per la piràmide gran molt més gran del que en realitat es necessita. I no tant sols això, els sobraran piràmides petites.
Ara els arguments eren uns altres: "hem de fer les piràmides petites amb el costat de la base més petit. Si la moneda de xocolata fa 3'5cm de diàmetre, en tenim prou amb un costat del quadrat de la base de la mateixa mida". La idea va ser molt interessant ja que estaven desenvolupant el concepte d'inserir un polígon en un cos geomètric. Per això la mestra ho va recollir i va continuar fent desenvolupar aquesta idea, fent-los adonar de la importància del moment matemàtic. L'eufòria del grup és manifesta i la motivació augmenta. La participació és cada cop més general, i això es nota, les idees avancen i cada cop són més complexes.
La conversa els porta a acords fonamentals pel grup. Les piràmides petites han d'omplir tota la superfície de la caixa que farà de continent de tot el contingut, les vint-i-quatre piràmides petites. La idea inicial comença a quedar obsoleta. Es poden repartir les piràmides per tots els costats: cada costat sis piràmides. Però l'agrupament no pot ser lineal, s'han d'apilar, s'han de fer pisos. Si es manté aquesta idea, la caixa final no tindrà forma de piràmide, continuarà essent un prisma.
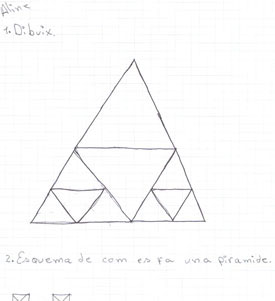
La mestra va intervenir proposant que provessin diferents formes d'apilar a la llibreta d'apunts personal. Tothom intenta dissenyar, individualment, com s'imagina el resultat final d'agrupar les piràmides en forma de piràmide. Comencen a sorgir les primeres propostes i es comencen a compartir amb tot el grup en els llençols. Les dificultats comencen a ser molt paleses. Els és molt difícil d'imaginar i dibuixar com es poden apilar les piràmides en forma de piràmide. En compartir les idees els sembla que potser seria més fàcil si ho fan apilant vint-i-cinc piràmides. D'aquesta manera, l'última piràmide podria fer més fàcil la punxa final de la piràmide gran. Aquesta no caldria que fos de la mateixa mida que les altres, tindria la mida que convingués per acabar de donar la forma exacta que necessités la piràmide-caixa. De passada, com que aquesta seria diferent i "sobraria", podria ser la que contingués l'enigma i els titelles.

Diferents propostes per apilar les vint-i-cinc piràmides en forma de piràmide-caixa
De totes maneres, s'està en una situació difícil. No aconsegueixen visualitzar i plasmar en el pla la situació de volum. Comencen a pensar que necessiten provar-ho amb d'altres materials. Alguns proposen construir unes quantes piràmides i anar fent diferents combinacions. D'altres pensen que es perdrà massa temps, caldria trobar uns materials que ens permetessin provar-ho sense tanta feina. A més, no saben com construir piràmides!. El problema és massa greu i les idees van molt ràpid: tenim el racó d'arquitectura. Si aprofitem la sessió de racons podem utilitzar les peces per fer proves i fins i tot construir el que calgui per assajar.
El fet de comunicar i la necessitat d'entendre la realitat els ha portat a haver de representar. Aquesta representació els ha ajudat a organitzar i transmetre les idees i els ha fet buscar altres maneres de representar per resoldre la situació problema.

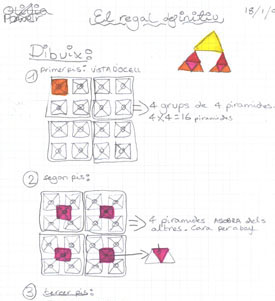
En el moment de la tria de racons es recupera la idea de l'activitat pel taller. En Biel i en Xavi agafen la responsabilitat d'anar a investigar per poder desenvolupar amb èxit el projecte de tot el grup. Els P.G.G. els donen la confiança i deleguen en ells la responsabilitat d'aquesta tasca. En l'activitat del racó es troben amb el context ideal per a poder experimentar. Troben unes peces amb encaixos que els serveixen per desenvolupar totes les estratègies que havien estat discutint a l'aula. Al final de la sessió de racó aporten una nova proposta al grup. En la sessió de devolució de racons exposen la seva idea que pot ser la solució:

"Les podem apilar en quatre pisos. En el primer pis fem quatre grups de quatre piràmides, plantades, cadascun. Quatre més en el segon pis, cap per avall. Quatre en el tercer pis, plantades. I, en l'últim pis, la que contingui l'enigma que haurà de ser amb les cares en forma de triangles isòsceles. Així, tindrem vint-i-cinc piràmides agrupades en forma de piràmide".

Tant en la situació de racó com en la posada en comú a l'aula, el grup va tenir l'ocasió de compartir coneixement i avançar en l'aprenentatge i en comunitat. En aquest cas l'eina fonamental que ho va permetre va ser l'ús de la visualització i el raonament matemàtic i la modelització geomètrica per resoldre el problema.

S'havia resolt una de les problemàtiques. Ara calia descobrir com construir les piràmides.

Volem construir piràmides

S'enceta la discussió a partir de les proves que han fet els companys del racó. La majoria de les piràmides les van fer amb les peces de colors i encaixos però quan es van acabar van utilitzar trossos de cartró tallats a la mateixa mida de les peces. En veure aquesta producció alguns companys en fan la crítica ja que es valora com a una feina poc rigorosa. Cal fer les piràmides molt perfectes per tal que puguin encaixar les unes amb les altres i la pila quedi perfecte. Després de parlar-ne molt decideixen que tenen poca informació i que els cal assessorar-se millor. Ho buscaran a nivell individual durant el cap de setmana. Cal tenir informació sobre:

- característiques de les piràmides
- classificació i tipus
- desenvolupament
- superfície
.....

En la sessió de posada en comú es veu que hi ha molt d'interès. Han recollit molta informació i ara cal tractar-la. Es posen per grups taula i comparen els materials i documents. El llistat podria ser el següent:

- diferents piràmides desplegades
- enciclopèdies matemàtiques
- llibres de text de diferents edats
- propostes de desenvolupaments de les famílies
- propostes de construcció pensades pels propis alumnes

Un cop es va recollir per grups, es va compartir amb tota la classe. La idea central que es va desenvolupar va ser sobre com dibuixar una piràmide regular de base quadrada. La discussió va girar al voltant de quatre propostes:

- anar comparant les mides amb un regle i fer el desplegament

- a mà alçada

- amb el regle i el transportador

- amb l'escaire i el cartabó, el regle i el compàs

De totes les propostes, la que es va veure més ràpida i econòmica (se n'havien de fer vint-i-cinc) va ser aquesta última. L'Alejandra va estar encantada de compartir amb tot el grup el seu coneixement. Ja havien tornat a avançar com a comunitat d'aprenentatge. El millor de tot era que ara s'obrien nous camps d'investigació a nous coneixements:

- la mesura de les piràmides
- la tecnologia i les eines
- les diferents classes de piràmides
- el treball cooperatiu
- ...

La mesura de les piràmides

La conversa continua i cal concretar la feina. Es proposa un treball individual pel cap de setmana "pensa quina alçada vols que tinguin les piràmides petites sabent que:

- la base és un quadrat
- un costat de la base mesura igual que el diàmetre de la moneda de xocolata
- les cares són triangles equilàters"

També es proposa que investiguin sobre els materials, els colors... de les piràmides individuals, de la piràmide de l'enigma i de la piràmide-caixa.

Pel retorn, s'organitza l'aula en petits grups d'interessos. Cada grup està format per persones interessades especialment en resoldre la problemàtica de cada situació:

- la piràmide-caixa
- la piràmide per l'enigma
- la piràmide de la moneda

El grup de les piràmides més petites, per les monedes de xocolata, comença a fer proves amb diferents materials. És un grup que té les mides pactades i acordades, només han de seguir la mida del diàmetre de la circumferència i utilitzar-ho per la base quadrada i les cares dels costats dels triangles equilàters. Decideixen fer les piràmides de cartolina de color terrós.

El grup de la piràmide-caixa fa els càlculs de la base de la piràmide a partir de la mesura del costat de la base de la piràmide petita, sumen tots els costats de les quatre bases i ja tenen la mida del costat per calcular la base de la piràmide gran. En aquell moment s'adonen que necessiten saber l'alçada de la caixa i decideixen consultar al grup de la piràmide enigma. Poden prendre la decisió del material. Faran les arestes amb llistons de fusta i les cares amb paper transparent.

El grup de la piràmide de l'enigma té un problema. Pensen que la seva piràmide no pot ser regular. Ha de tenir l'alçada justa per encaixar en la piràmide-caixa, just a partir de l'últim pis. Van fent diferents proves amb diferents mesures. Tenen la mesura del costat de la base del tercer pis però no saben com han de ser les arestes per coincidir amb el vèrtex de la piràmide-caixa. Les diferents experimentacions i proves els porten a fer un descobriment mot important. Cada vegada que construeixen una piràmide, sigui de la mida que sigui, la seva alçada és una unitat de mesura més petita que un dels costats de la base. Per això decideixen aplicar-ho i generalitzar-ho a la seva piràmide. El resultat va ser el següent:

- la base serà un quadrat de 11,5cm de costat
- les cares seran triangles isòsceles. Els dos costats més curts mesuren 10,5cm i el més llarg mesura 11,5

Per tant

A partir d'aquí tots els grups van utilitzar aquesta descoberta per acabar de realitzar els seus càlculs.
La situació va ser molt rica. Es va crear una situació a partir de la necessitat de compartir experiències per establir acords i prendre decisions encertades i operatives, reals i, per això, decisives.
Una altra vegada s'havia produït l'aprenentatge en comunitat.

Però els problemes no van acabar aquí.

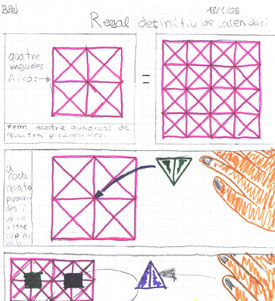
El grup de la piràmide-caixa va tenir un error de càlcul important. La pila de piràmides ni hi cabia. Se'ls havia acabat el temps i no tenien marge per tornar-la a construir. Decideixen utilitzar les peces d'encaixos de colors per fer de caixa.

Aquestes peces els tornaven a solucionar el problema. Per la mida de cada peça han de canviar altra cop els càlculs. Quedarà una mica més gran però decideixen tirar endavant. La construcció de dintre la deixaran ben fixada amb cintes adhesives i damunt d'una base de plàstic perquè aguanti bé.
Per resoldre-ho definitivament han passat per l'argumentació i la prova, han hagut d'utilitzar diferents tipus i mètodes d'argumentació així com desenvolupar i avaluar aquestes proves i arguments.
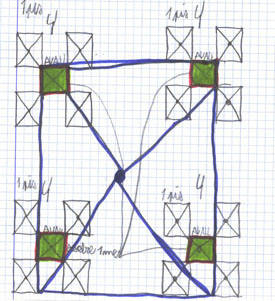
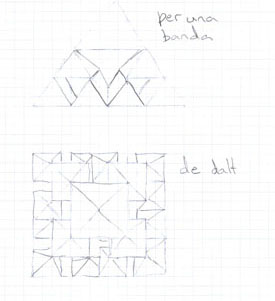
El marc de comunicació que s'ha viscut els ha permès analitzar i consolidar el pensament clarament i coherentment i, tot això, utilitzant el llenguatge matemàtic. És interessant veure diferents exemples de representacions dels càlculs:

En ells es posa de manifest la complexitat de la situació i les diferents maneres de representar-la: més descriptiu, més lingüístic, més simbòlic, més analític... però tots ells rics, dinàmics, amb significat, tant personal com de grup. Una vegada més s'evidencia que quan hi ha unes intencions, en aquest cas per part de l'ensenyant, les idees es transformen en nous coneixements.

És en aquesta línia que la mestra va continuar el procés demanant una valoració del treball realitzat. Una de les qüestions que surten en el debat és si en aquest moment tindrien tantes dificultats com a l'inici del disseny del regal per representar la pila de piràmides. Els proposa que ho intentin a nivell individual i que argumentin la seva representació. Els resultats van ser espectaculars. Gràcies a la comunicació, a l'intercanvi, a la interacció i a l'ús social i cultural del llenguatge matemàtic l'aprenentatge havia resultat un èxit per la totalitat del grup.
Podem comparar aquestes produccions amb el primer llençol de propostes per apilar les piràmides:

Ja hem dit en altres moments d'aquest treball que el creixement personal de cada criatura depèn del propi nen o nena, però també de la naturalesa de les experiències en les quals aprèn a mirar el món i a situar-se en ell. Si les activitats de l'aula estan fonamentades en situacions reals s'utilitzen dades i informacions reals i es pot conèixer la realitat a la vegada que s'aprenen nous coneixements.
Les interaccions entre les persones han fet possible que la interpretació de la realitat hagi produït aprenentatges matemàtics. La mestra va saber plantejar el procés del treball. L'alumnat va poder viure experiències adequades, on es va poder experimentar i aprendre el paper que juga la comunicació en els processos de resolució de problemes que van permetre construir una visió nova de les coses i de la realitat.

Per acabar, calia un bon moment d'aturada, de reflexió, tant individual com conjunta. S'havien de posar de manifest les intencions i els objectius de les persones que havien interactuat a l'aula. Les dels alumnes, fent un bon i rigorós regal als companys de 3r. Les de la mestra, compartint un aprenentatge, aparentment matemàtic, entre tota la comunitat i transformar-lo en un aprenentatge social molt més ampli, passant per processos comunicatius importants per les persones. D'aquí la importància de què tothom pugui controlar els processos. En finalitzar el treball se'ls demana que ho reflecteixin tal i com ho han viscut i ho fan d'una forma molt clara i entenedora per tot el grup. L'esquema final del procés va ser el següent:

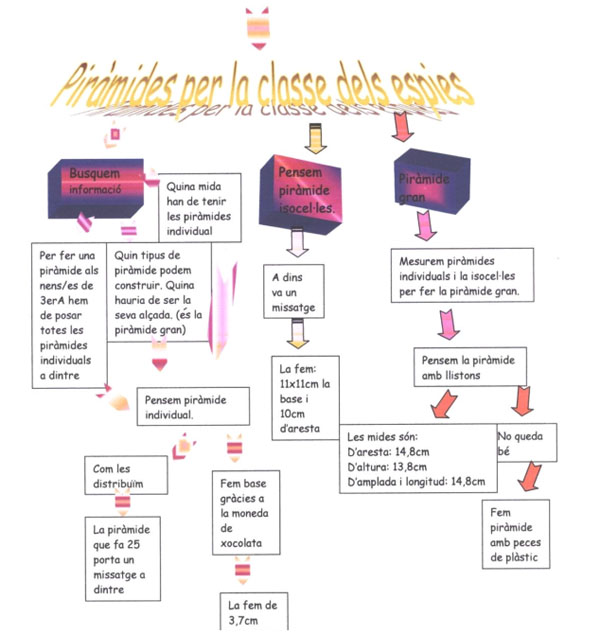
El regal va ser tot un èxit. Les emocions es van desbordar. L'esforç havia valgut la pena.