A l'escola, dins l'horari setmanal de totes les classes figura un espai anomenat "Taller de festes" que, com el seu nom fa pensar, serveix per donar cabuda a totes les activitats que la preparació de les diferents festes (Castanyada, Nadal, Festa Major, Carnaval, Sant Jordi, Final de curs) genera.

Respon al desig de donar molta rellevància a uns moments, les festes , que unifiquen l'activitat de tots els alumnes des dels més xics fins als grans, uns moments rics en convivència entre les diferents edats, en intercanvis i en participació de les famílies (tan en el disseny i organització com en la col·laboració per a la seva posada en pràctica o la participació en el que és la pròpia festa).

La preparació de les festes a cada classe és una font inesgotable de creació de necessitats, en la resolució de les quals es veuen implicades totes les àrees del currículum. Les activitats que es realitzen són de debò, i la força de la realitat potencia al màxim el seu significat per als nens i nenes. Cal, però, defugir de les presses, que les festes comencin a preparar-se amb el temps suficient. I tan és així que a la setmana d'haver celebrat una festa, ja estem pensant en la següent. De fet no és tan estrany si pensem en el que passa a la societat amb els col.lectius que organitzen les festes rellevants: comencen a preparar-les amb un any d'antelació!

Aquesta història comença dins d'aquest marc de Taller de Festes.
Es tracta en aquest cas de la festa de Nadal i d'una de les activitats que dins d'aquesta festa realitzem: El calendari d'Advent.

Quan comença el mes de desembre el calendari d'Advent passa a presidir el vestíbul de l'escola (foto). Es com els calendaris d'Advent que es poden trobar al mercat, amb les seves finestretes de cada dia que amaguen sorpreses a dins. La seva mida és gegant: cada dia és una capsa de cartrò tancada i amb el número a la tapa.
Cada classe sap quin dia li toca obrir la porta i quedar-se el regal que amaga i quina altra capsa ha de preparar per als nens d'una altra classe.
Sempre ens ha donat bons resultats deixar els números "dificils", 11,12,13... per als més petits. És una forta motivació per aprendre a esperar i de passada aprendre el nº.

Aquest any a la classe de 5è A ens ha tocat obrir la caixa del dia 9 i preparar la caixa del dia 19, que serà per als nens i nenes de 5 anys, de la classe dels avions.

Aixì doncs dediquem la primera sessió (dues hores) d'aquesta història a decidir quin regal volem fer per als "avions".

Propòsem als alumnes agrupar-se lliurement en grups d'entre 3 i 5 alumnes. Cada grup haurà de presentar un o més projectes sobre els que estiguin tots d'acord. Un representant de cada grup farà desprès les propostes a tota la classe i entre tots decidirem quin regal els farem . És importantíssim que pensin en la viabilitat de les propostes i en l'edat dels nens als qui va dirigit el regal.

(Buscar la coherència del pensament dels altres és una constant de la nostra manera de treballar, és el que ens permet nodrir-nos de la Diversitat. Veurem molts exemples pràctics dins l'aula més endavant. Aquí vull destacar que les festes provoquen moltes situacions que demanen a l'alumne posar-se al cap d'altres companys d'edat molt diferent a la seva i intentar comprendre què els agrada, què els interessa, què poden fer i què no, com pensen...)

Podem fer una proposta inventada o que ja saben, i en aquest cas cal que facin els dibuixos pertinents, o una proposta que han trobat en un llibre dels racons de l'artista o d'arquitectura, i llavors han de dur el llibre i ensenyar-nos de què es tracta. Limito el temps de que disposen i comencem a treballar en grups.

Treballen força bé, de manera molt autònoma. Cap grup em demana ajut, només volen compartir amb mi les seves propostes, satisfets d'haver-les trobat. Tots els grups prefereixen buscar les propostes als llibres dels racons i generalment en troben més de una, un grup de nenes van fer un llistat de set propostes!

Quan el temps s' ha acabat ens reunim a la classe i van exposant les seves idees. Jo les apunto a la pissarra i un cop les han vist totes hi ha vàries intervencions a favor o en contra d'algunes d'elles.

Proposo una votació especial, ja que hi ha moltes idees: cada alumne podrà votar-ne tres: la que més li agrada amb 15 punts, la segona amb 10 i la tercera amb 5. No és obligatori votar-ne tres, si algú té molt clar quina vol millor que voti només la primera i no faci servir els altres punts .

La votació resulta apassionant i molt interessant des del punt de vista del càlcul, jo els dic que controlin si m'equivoco i ja ho crec que ho fan! També és molt interessant com anticipen en quin moment de la votació el resultat ja està decidit.

Hi ha dues propostes molt destacades de la resta: "Les butxaques texanes", que ha guanyat i "Les medalles" (foto).

Acordem que farem les dues coses, ja que "Les butxaques texanes" ha de ser un regal col·lectiu i a aquests nens tan petits els agradarà molt també poder tenir una cosa personal com és el cas de les medalles . Acordem que en comptes d'un animal com proposa el llibre, el motiu de la medalla serà un avió, ja que segur que els agradarà molt perquè han triat aquest nom per a la seva classe.

A partir d'aquest moment comença la Història de les medalles que ,com podreu veure ens va donar moltes satisfaccions personals i moltes oportunitats de treballar la matemàtica en un context molt significatiu per als nens i nenes de cinquè.

Encara vam fer una feina final aquest primer dia: decidir quins materials necessitaríem i la seva quantitat i veure quins teníem a l'escola, quins podríem portar de casa i quins hauríem de comprar.

Presentació de l'activitat

Recordo als nens i nenes que la sessió passada vàrem decidir que per a cada medalla faríem servir 28 cm de cinta però ara ens cal saber quanta cinta necessitem en total. Ells saben que a la classe dels avions són 25 alumnes però jo els recordo que em van dir que per la mestra també li volien fer medalla per tan n'hem de fer 26.

Els dic que ho calculin en un full que repartim i que quan ho hagin fet passin a calcular el que diu a la segona part del full: quant ens costarà. Que no sabem a quant ens costarà el m però que l'any passat jo vaig comprar una cinta que em va costar a 23 cèntims el m (escric a la pissarra 0,23 ?) i podem utilitzar aquesta dada per fer-nos una idea del que ens pot costar.

Que poden fer els càlculs de la manera que vulguin. Que les calculadores les poden fer servir per a comprovar els resultats o com a últim recurs si no se'n surten, però que en aquest cas anticipin, pensin abans quin és el resultat que estimen que els donarà i sobretot analitzin si el resultat que ens marca la calculadora és un resultat possible (és fàcil equivocar-se al pitjar els botons).

Realització de l'activitat

El primer problema el resolen sense cap incident remarcable: necessitarem comprar 7,28 m de cinta. No apareixen càlculs personals, ja que saben fer la multiplicació convencional. Els tres nens que tinc amb dificultats específiques de càlcul passen directament a la calculadora. Dels altres alguns comproven i rectifiquen si cal. D'altres no comproven el resultat. Crec que hi ha els dos extrems: els que estan segurs d'haver-ho fet bé o els que desconfien del que han fet (alguns no saben bé les taules, altres encara no controlen l'algorisme)

El segon problema és ben diferent. També es tracta d'una situació de multiplicar però els factors tots dos són decimals. En alguna ocasió havien fet alguna multiplicació on apareixia algun factor decimal (euros amb cèntims) i l'havien resolt espontàniament expressant els diners en cèntims (la qual cosa eliminava els decimals) i després passant el resultat de cèntims a euros.

Al cap d'una estona sento el neguit que es va generant i demano que parin de treballar individualment i comentem què els passa entre tots.

A.- " No sé fer aquesta multiplicació. No puc imaginar-me com es poden multiplicar dos decimals. No ho entenc"
Mestra- " Algú té alguna idea".
P.- "Podríem separar els m i els cm i calcular les dues coses per separat "
Mestra- " Qui vol dir més coses?"
No hi ha cap paraula així és que els animo a continuar el càlcul tenint present , si els va bé la idea de P.
Hi ha un grup que fa càlculs per aproximació i d'aquests només un arriba al resultat final, el de la J. , el podeu veure a continuació (aquest treball donarà origen a la sessió següent, com s'explica al següent capítol)

Càlcul de la J. Per saber quant costarien 7,28 m de cinta a 0,23 el m:

Hi ha d'altres nens que fan l'algorisme però no saben què fer de tants decimals. Altres acaben buscant el resultat a la calculadora.

Quan la majoria han acabat fem una posada en comú dels càlculs que han fet i les dificultats que han tingut. Hi ha molt d'interès per saber com es deu fer aquest algorisme i decideixo fer-lo a la pissarra.
"És veritat que aquesta multiplicació era diferent de les que heu fet fins ara. Alguns nens i nenes han calculat el resultat sense fer la multiplicació...es pot fer de moltes maneres.

Els grans la fan amb la calculadora si en tenen i si no fan la multiplicació d'aquesta manera que ara farem a la pissarra. Tots m'ajudareu i, si voleu ,la podeu copiar al costat dels vostres càlculs. Si ho feu marqueu bé la separació i ningú esborra res del que ha fet, ja que tot és molt important. Recordeu l'anècdota d 'Edison que us vaig explicar l'altre dia.

(L'anecdota d'Edison:

Aquesta anècdota la vaig sentir per la ràdio i la vaig explicar als nens i nenes perquè alguns esborraven el que havien fet quan veien que no arribaven a la solució. Sovint en faig referència.

"Una vegada un periodista va preguntar a Edison com anàven les seves investigacions sobre l'electricitat i ell va contestar que anaven molt bé i estava molt satisfet.
Llavors el periodista va pensar que havia fet un descobriment molt important i li va demanar que li expliqués per poder publicar la notícia al seu diari.
Davant la seva sorpresa Edison li va dir que no havia descobert res encara però que anava per molt bon camí ja que havia fet 800 experiments sense èxit i per tant ja havia descartat 800 hipòtesis que ja no el destorbarien i segur que ja estava molt a prop de la vertadera.")

Passo a fer la multiplicació i veig que tots estan molt interessats a copiar-la.
Mestra- " És veritat que ens costa entendre què passa amb els decimals quan multipliquem com abans ha dit A. Els matemàtics van pensar una manera de facilitar els càlculs i així ho fem normalment els grans si no tenim la calculadora a la mà: abans de fer la multiplicació treuen les comes fent el nombre deu, o cent o mil vegades més gran (alguns de vosaltres també ho fèieu quan abans de multiplicar passaven els euros a cèntims). Però després ho hem de compensar al resultat fent-lo deu o cent o mil... vegades més petit. Si els decimals són als dos factors traiem els decimals de tots dos i després hem de fer una doble compensació al resultat
Si trec la coma de 7,28 en quina quantitat es converteix?"
Alumnes- "728"
Mestra- "Quantes vegades l'he feta més gran aquesta quantitat. Per quant he multiplicat?"
No està gens clar. Algú diu per cent però veig que la comprensió és molt minoritària.
Faig la mateixa pregunta amb el 0,23. Aquí s'afegeix la dificultat del 0 al davant però veig que per alguns no és cap problema, en canvi d'altres es limiten a "escoltar".
Entre tots anem multiplicant i al final compensem el resultat.
Mestra- " Ara hem de fer el resultat cent vegades més petit pel 7,28 i altres cent vegades pel 0,23. Dividirem per cent i una altra vegada per cent"
P. diu que per 10.000
Ningú sap com fer-ho. Els pregunto com feien per passar de cèntims a ? i això ens dona la pista per fer la primera compensació. La segona costa més de veure. Sóc jo la que continuo desplaçant la coma dos llocs més.
Veiem el resultat amb quatre decimals. Els pregunto si tenim monedes tan petites i em diuen que no. No aclarim el valor que tindrien de aquestes monedes si existissin, expressament no m' hi aturo en aquest problema ja que crec que és millor fer-ho en una altra situació on aquestes unitats més petites tinguin més significat (pocs dies després sortiria el tema del nombre Pi).
Mestra- "Com que no hi ha monedes tant petites hem d'arrodonir el resultat. Quants diners seran?"
Alumnes- "1,67"
Mestra- "Teniu raó. Aquest seria un bon arrodoniment, ja que la xifra següent és un 4 està més a prop de 1,67 que de 1,68. Si fos un 7 o un 6 estaria més a prop de 1,68. ( ho dibuixo a la pissarra). No sabem com ho arrodoniria el botiguer, potser ho faria cap el 1,68 per no perdre diners..."

Reflexions sobre l'activitat

Uns continguts lligats a les necessitats de la vida a l'aula

Després d'haver fet l'activitat repasso la gran quantitat de continguts del currículum que hem fet servir (m, cm, ?, cèntims, sistema de numeració, nombres decimals, multiplicació, proporcionalitat, estimació, arrodoniment...). Alguns d'ells no els havia previst abans com és el tema de l'arrodoniment de quantitats.
Tots aquests continguts tenen el valor inestimable d'haver aparegut dins un context significatiu per als nens i nenes. De debò ens han servit per a solucionar situacions de la nostra vida a l'aula, situacions semblants a les que els adults han de solucionar fora de l'escola. Els alumnes es van fent la idea d'uns continguts matemàtics lligats a situacions més àmplies i globals on aquells en són un bon instrument per a poder-les controlar i comprendre.
Quan treballem les àrees de forma globalitzada de vegades tenim por de que hi hagin buits en els aprenentatges dels alumnes, de que algun contingut se'ns escapi i no aparegui. És cert que hem de portar el control del que es va treballant a l'aula però sempre resulta més fàcil del que a priori pugui semblar, ja que els continguts importants surten constantment , lligats a situacions ben diverses. El paper del mestre està a triar la situació que sembli més adient per aprofundir en aquell o altre contingut.

Estratègies pròpies dels alumnes i algorismes convencionals

En el nostre Projecte de Centre les estratègies de càlcul de nens i nenes són molt importants. Més endavant, en aquest treball s'aprofundeix sobre el tema però aquí voldria destacar la diferència entre el primer i el segon exercici de l'activitat proposada.

En el primer cas, el càlcul és molt més senzill. Els nens saben fer l'algorisme convencional (l'hem après aquest curs, 5è). Es tracta d'un exercici semblant a la majoria dels que s'han fet durant molts anys a les escoles. Els nens apliquen el mecanisme (bé o malament). La diversitat resultant, les idees que emergeixen són ben pobres, més aviat inexistents.

En el segon cas cal multiplicar dos nombres decimals i els nens no ho saben fer. Aquesta situació més complexa dóna peu a l'aparició de les estratègies personals de cadascú. Totes aquestes estratègies posen en joc un tempteig íntim amb les quantitats, amb el sistema de numeració, amb la qualitat de les quantitats, amb el sentit de les relacions...que necessàriament fa avançar el pensament matemàtic dels nens i nenes.

D'altra banda els nens i nenes tenen molt d'interès per als algorismes convencionals. L'escola ha de contenir i donar sortida a les inquietuds de les famílies per això cal explicar molt el sentit del que fem i donar a conèixer quan tenim previst treballar cada algorisme convencional, transmetent la idea de que al final els sabran tots però, pel camí recorregut, sabran molta més matemàtica que si d'entrada els hi haguéssim ensenyat sense més ni més.

Presentació de l'activitat

Mestra- "He estat mirant els càlculs que vàreu fer ahir per saber quant hauríem de pagar per 7,28 m de cinta si cada metre valgués 0,23 ?.
Alguns nens i nenes varen dir que era un càlcul difícil però malgrat això tots ho vàreu fer força bé. Alguns alumnes no van arribar al preu exacte però es van aproximar molt.
Avui el que farem és que entre tots mirarem el que va fer un de vosaltres i intentarem comprendre què és el que va fer per a calcular. He triat el treball de la J. , un altre dia triarem el d'un altre nen o nena. Fixeu-vos que la J., en el seu full, no només fa números, també fa altres signes (fletxes, cercles, dibuixos, signes d'interrogació...). Tot plegat ens pot ajudar a entendre què és el que ella anava pensant quan calculava.
Primer copiaré el seu treball a la pissarra i entre tots anirem pensant com va calcular. La J. ens podrà anar dient si ho encertem o no. Després repartirem una fotocopia del seu treball a tothom perquè cadascú ho expliqui a la seva manera. Vigileu, que al full també hi ha la multiplicació que vàrem fer després, està separada per una línia vertical i aquesta no s'ha d'explicar."

Realització de l'activitat

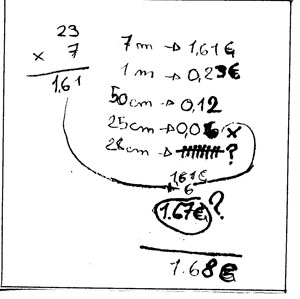
Copio a la pissarra el treball i vaig preguntant per on va començar, per què els sembla que multiplica 23x7, què representa la taula del costat amb les fletxes, com la va fer aquesta taula, què deuen significar els dibuixos, i els interrogants, quin és el resultat...
Entre tots van sortint les respostes i la J. va dient que sí:
-"Ha començat fent la multiplicació i ha separat els m i els cm, per això només multiplica per 7, que són els 7 m"
-"Multiplica per 23 i no per 0,23 perquè multiplica pels cèntims i després el resultat el posa en euros: 1,61"
-"La taula del costat la fa per buscar quant valen els 28 cm"
-" Va calculant cada cop la meitat fins a 25cm que valen 0,06 ?"
-"No sap quan valen els 28 cm. Dibuixa 8 pals però no ho sap i els tatxa i posa un interrogant"
-" Es que és molt poc: si 25 cm valen 0,06 ?, 3 cm de més que té 28 no arriba ni a un cèntim per això es queda amb el preu dels 25 cm"
-"Després suma els 6 cèntims al preu dels 7 m i li dóna 1.67 ?"
-" El resultat és 1.68 ? perquè el botiguer no vol perdre diners"

Molts nens i nenes no han participat del debat però han estat atents aparentment. Tinc curiositat per veure que faran al full. Repartim el treball de la J. i els dic que posin de títol "Idees de la J."; que al full poden fer el que vulguin: escriure a sota, al costat, fer fletxes... tot el que els sembli que representa millor el que ells pensen.

Reflexions sobre l'activitat

- Els càlculs de la J.

Quan vaig veure el full de la J. em vaig quedar meravellada del que aquesta nena havia estat capaç de fer, del pla que havia dissenyat i havia seguit fins al final controlant en cada moment el significat del que anava fent. La majoria dels aspectes del seu "text de calcular" van ser analitzats molt bé per els seus companys i ja s'han explicat però jo encara destacaria el domini que mostra del sistema de numeració quan calcula amb xifres decimals, per exemple no té cap dubte sobre com sumar els 6 cèntims dels 28 cm als 1,61 ? dels 7 m.; o fa sense problemes la meitat de 0,12 : "0,06".

Vaig decidir que tota la classe ho hauria de compartir. Per sort no havíem analitzat encara cap treball d'ella. Els alumnes saben que fa les coses molt bé i em fa por que es desanimin o que es despertin sentiments de gelosia si n'abusem.
Em representa una preocupació buscar aspectes en tots els alumnes que puguin ser interessants per a la resta però normalment els trobo, ni que sigui en altres activitats.
També pensava si els alumnes més immadurs podrien comprendre el que la J. havia fet, per això ho vàrem comentar primer tots junts.

- La comprensió de les idees de la J. per part dels seus companys

La meva primera sorpresa agradable va ser que tots poden dir alguna cosa sobre el que la J. ha fet. Segurament ha influït el debat previ. Em quedo amb el dubte de què hagués passat si d'entrada els dono el full per a la seva interpretació de manera individual de manera individual.
He seleccionat una mostra de treballs de nens i nenes que reflecteixen com sempre la gran diversitat de l'aula. En primer lloc copio el que diuen alguns alumnes que es limiten a escriure al peu del full el que pensen:

a).- "Ha anat fent la meitat dels números"
b).- " La J. ha fet primer 7 metres i ha deixat els 28 cm i els ha anat restant fins que li ha donat el resultat"
c).- "La J. parteix 7.23 en m i cm. Primer ha buscat el preu de 7 m, ha multiplicat 23x7. Després volia trobar quant valien 28 cm i ho ha aproximat"
d).- " Els 7 metres són del 7,28m que valen 1,61?. 1 m val 0,35?. 50 cm són la meitat de 1m, que val 0,12 ?. Els 25 cm són la meitat de 50 cm, que val 0,06?"
e).- "Això sembla el que vaig fer jo. La J. ha anat fent la meitat fins a 28 però li ha donat 25 i ja es passava. Llavors era tan poca la diferència que només li ha afegit un cèntim"
Els exemple f), g) i h) són treballs on els alumnes manipulen el treball inicial de la J.per a fer les seves pròpies observacions (estan repassades en vermell per distingir-les millor)

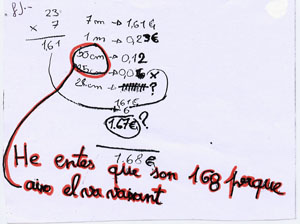
F)

G)

H)

La diversitat és ben patent en els dos tipus de treballs. El grau de comprensió és molt diferent i, malgrat aquest fet, el treball de la J. passa a ser patrimoni de la classe i enriqueix de maneres diverses a tots els membres de la comunitat d'aprenentatge.
Si anem analitzant una per una les diferents respostes sempre hi ha coherència encara que ens puguin semblar molt parcials o poc precises .

El treball f), per exemple, és segurament el que mostra un nivell menor de comprensió, diu ben poqueta cosa. Intento comprendre i valorar el contingut d'aquest tipus de treballs en lloc de pensar en què li falta, això sempre em dóna bons resultats com a mestra ja que sempre trobo motius per sorprendre'm i respectar el que fan els alumnes.
En primer lloc ja és molt que s'hagi atrevit, sense por, a dir la seva davant d'un treball d'una alumna tan brillant. Segurament la seva ment ha estat recorrent el text de càlcul cercant activament relacions entre els components...ha entès perfectament quin és el resultat, pensa que, per arribar-hi, la J. ha fet un càlcul complex, que és a l'espai de dalt. Ell intenta comprendre aquest càlcul i troba com a significatives dues quantitats: 50 i 25, de seguida comprèn que la J.,el que fa en aquesta columna és manipular aquesta quantitat "el va baixant".
Segurament hi ha moltes altres coses que les intueix , encara que no les expressa: la manera com "baixa" les quantitats (fent meitats), la relació entre les dues columnes de la taula , el procés seguit per la J. (com a mínim que ha seguit un procés) ...

De la mateixa manera podríem analitzar els altres treballs i fer l'esforç de pensar que ha suposat per als autors en cada cas. Sempre ens trobarem amb una gran esforç per apropiar-se del pensament de la J., cosa que és possible perquè el que la J. ha fet és coherent i la ment de tots els alumnes de l'aula també ho és.

El grup viu aquest tipus d'activitats com una oportunitat d'enriquiment personal molt gran. Em va sorprendre la proposta d'una nena que va acceptar tot el grup:
"Al títol de l'activitat - Idees de la J.- podríem afegir el nostre nom:- Idees de la J. i del/ de la.....................- , ja que si entenem el que ha fet també són idees nostres"

- Els treballs de nens i nenes com a objecte d'estudi, una bona eina per aprendre en la diversitat

Les activitats que es fan a l'aula a partir dels treballs d'un alumne o grup d'alumnes tenen com a conseqüència immediata la vivència de que el que els nens i nenes fan i pensen és important per a la comunitat d'aprenentatge. Ens poden ser tan útils com la informació que podem trobar a un llibre, com el que pugui explicar un mestre , com el treball personal ...per ajudar-nos a aprendre.
Es necessari però, haver creat un clima previ que afavoreixi l'expressió de les idees pròpies, el respecte cap als altres i la confiança en que totes les idees ens fan avançar, ja que, si més no, posar-nos al cap d'un altre per saber com pensa és un bon exercici mental .
El contrast de les idees pròpies amb les del altres no tindria com a objectiu primer que els alumnes avancin en veure altres produccions més elaborades , cosa que pot succeir i de fet es produeix freqüentment. L'objectiu més important és fer créixer la racionalitat com a valor de la comunitat que aprèn, una racionalitat que busquem en la coherència dels pensaments diversos i no en una única manera de pensar, la dels continguts oficials.

Reflexionant en el procés de l'activitat d'aquesta sessió, tenim una situació inicial on els alumnes són molt diversos. L'activitat ens permet que tots participin d'un objectiu comú com a comunitat, entendre el treball de la J. La manera com aquesta activitat incideix en cada nen i nena és també molt diversa però tots participen i tots avancen.
En aquest cas el treball presentat era d'una gran qualitat però aquest fet no és necessari, fins i tot crec que seria contraproduent presentar sempre els treballs de més alt nivell. Es fàcil anar variant el nivell sempre i quan anem a buscar la coherència i no les falles. Crec que ,en canvi, sí que pot ser positiu proposar als nens que completin o acabin el treball d'un company quan hi ha una proposta interessant que no s'ha pogut acabar.

- Puc entendre el càlcul del meu company, em sento autònom, confio en el meu pensament

Dins la situació escolar intervenen molts elements no explícits que incideixen d'una manera molt important en la dinàmica de l'aula. Quan fem una pregunta als alumnes ells de seguida intueixen què volem:
a- Que ens contestin una resposta concreta, la bona, la acabada, la oficial...
En aquest cas deixarem al marge una bona pila d'alumnes, que no saben la resposta i, el que és més important: els alumnes creuran que a l'escola no és important pensar sinó dir el que el mestre vol sentir.
b- Que ens donin una resposta personal, d'acord amb les seves idees, que el que pensen és important per fer avançar tota la comunitat d'aprenentatge.
Només en aquest segon cas aconseguirem un grup creatiu, participatiu on la diversitat es respecta i es viu com un factor positiu que enriqueix a tots.
Només en aquest cas els alumnes confiaran en les seves possibilitats i afavorirem la seva autonomia, fins i tot davant el que puguin dir els llibres o els adults.

Presentació de l'activitat

Explico als alumnes que he anat a la merceria a comprar les agulles imperdibles i la cinta per fer les medalles.

D'agulles imperdibles no he pogut comprar les 26 que necessitàvem perquè les venien en paquets de deu (vegeu la fotografia ).

Pregunto si saben quants paquets he hagut de comprar i de seguida alguns diuen que tres i ningú protesta. Pregunto quantes agulles ens sobraran i de seguida diuen que quatre.

També els explico que no tenien cintes de quadres com els models del llibre. Havien de ser de seda i eren una mica més cares del que havíem pensat. He comprat cinta de dos colors (blava i vermella) per poder triar cadascú el color que més els agradés; i he comprat quatre metres de cada color ( una mica més del que necessitàvem per si hi havia algun incident i algun tros no es podia fer servir).

Mestra -" Ara repartirem un full per cadascú on hi ha la fotocòpia del tiquet de compra. Comprovarem entre tots el preu de la cinta i les agulles"

"Com és que posa tres cops agulles?"
Alumnes- " Han comptat cada paquet de deu per separat"
Mestra- "Quant val cada paquet?"
Alumnes- " 35 cèntims"
Mestra- "En canvi la cinta l'han cobrat tota junta, quant han costat els vuit metres?"
Alumnes- " 3 amb 20 cèntims"
Mestra- "Quant he hagut de pagar per tot?"
Alumnes- "4 ? amb 25 cèntims"

Proposo als nens de fer alguns càlculs a partir del tiquet:
En primer lloc calcular quants diners necessitaríem preparar si haguéssim de comprar diferents quantitats d'agulles (5, 48, 30...)
En segon terme calcular a quant val el metre de cinta si per tots 8 m ens han cobrat 3.20?.

Realització de l'activitat

Alguns alumnes em demanen poder treballar en parella o ajudar-se. Jo els dic que sí però que tothom ha d'entendre el que escriu al full, que es pot fer de moltes maneres i totes són vàlides si podem arribar al resultat i també ho són si no ens porten al resultat per què ja sabem un camí que no hem de seguir, que no esborrin res perquè tot és important i ens serveix per millorar la nostra manera de calcular.

Alguns treballen sols, normalment són els que se senten molt segurs. Algunes parelles s'ajunten espontàniament, el seu ritme és semblant i se senten còmodes treballant juntes. Alguns tenendificultats i demanen ajut als companys o a mi.
Alguns nens em demanen si poden utilitzar la calculadora. Jo els dic que provin sense i després la poden agafar per comprovar el resultat o bé per resoldre el càlcul si és massa difícil.
Respecte al càlcul del preu de les agulles imperdibles:
Veig que un alumne té dificultats per saber quants paquets de deu ha de menester en cada cas (treball 1), m'ha demanat que l'ajudi.
Li dic que dibuixi els paquets i no m'entén. Jo li dibuixo cercles i li poso 10 a dins i juguem a veure quants paquets compraríem si volguéssim 6 agulles, 18... Ell m'ho pregunta un cop i jo un altre...Veig que no pot comprendre quants paquets necessita per 18 agulles. Li dic que dibuixi les 18 agulles i les empaqueti de 10 en 10. Sembla que veu que necessita comprar 2 paquets ja que amb un li falten 8 agulles. Així ho va calculant al costat d'un altre nen que també té dificultats. Els dic que poden fer servir la calculadora i , entre tots dos, se'n surten.

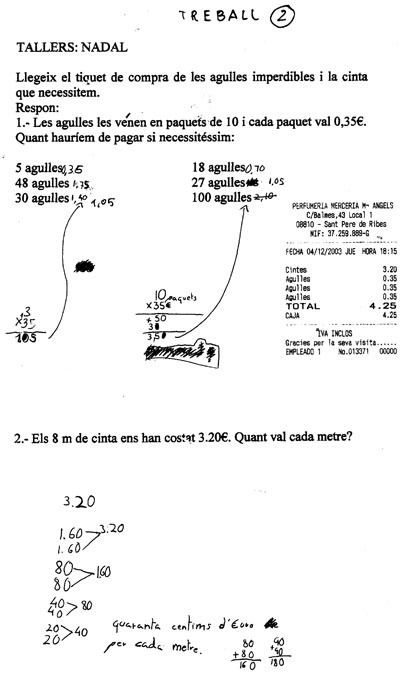
Els altres nens no tenen aquesta dificultat de saber quants paquets han de comprar. L'esforç el dediquen als càlculs. Depenent del nombre de paquets alguns fan el càlcul mentalment o amb la calculadora (treball 2)

El treball 3 em crida l'atenció per la facilitat per col·locar la coma entre els ? i els cèntims del producte de les multiplicacions malgrat als factors de l'operació que fa no n'hi ha ni una de coma. Sembla que multipliqui cèntims i després ho passa a ?. També multiplica pel nombre d'agulles i no pel de paquets, però després ho arregla traient un zero.

El treball 4 resulta interessant perquè intenta arribar al preu dels paquets establint una taula de correspondències entre paquets i preus...

Respecte el càlcul del preu d'un bon metre

Vegeu les dificultats que es mostren al treball 5. Es tracta d'una alumna nova a l'escola. Sap molt bé els mecanismes de les operacions i en canvi no comprèn les relacions entre les quantitats. M'ensenya la multiplicació que ha fet ràpidament i jo li dic que com pot ser que si 8 m valen 3.20?, 1 m valgui més. Es queda parada. Li dic que dibuixi els 8 m i que 3,20 és el preu de tots vuit i ella ha de calcular quant val un i que pot agafar la calculadora si vol. En acabar la sessió veig el seu treball però ja no li puc preguntar.

Veig que ha dibuixat els 8 m i no entenc que significa 23 cm (es possible que recordés que a la sessió anterior vàrem estimar que valdria cada m 23 cèntims? , potser ha girat l'ordre de les xifres 3,2?) La solució hi és però no massa destacada, per la qual cosa penso que no ho té massa clar encara.

La mateixa dificultat, fa una multiplicació quan ha de fer una divisió, apareix en el treball 1. Ha fet l'operació amb la calculadora. Li dibuixo els vuit m i li dic que 3,20 és el preu de tots 8 i ell ha de calcular quant val un. No sap què fer. Li dic que ha de repartir els 3.20 ? entre els 8 m per veure a quant li toca cada m. Em respon "dividir!" i ho fa amb la calculadora.

El treball 9 comença també fent primer una multiplicació (es tracta d'una alumna amb greus dificultats per al càlcul).

El treball 2 mostra un alumne que resol la divisió fent meitats fins que arriba a la vuitena part. A aquesta mateixa idea és la del treball 6, encara que la desenvolupa d'una manera més àgil. Una altra estratègia és la de anticipar el resultat i comprovar i ajustar. És el cas del treball 7 (és un nen que no sap bé les taules i se sent més segur realitzant agrupaments i sumes. Al final ha d'acudir a la calculadora). Jo li dic que quan aprengui bé la taula del 8 no haurà de treballar tant perquè sabrà que 8x4 són 32 .

També anticipa l'alumne del treball 3 i comprova multiplicant. Aquesta nena només col·loca les comes als resultats però sap molt bé el que es fa.

El treball 4 comprova la seva anticipació de dues maneres: multiplicant i fent una sèrie de dobles.

Una nena fa la divisió (treball 8 ). Sap el mecanisme perquè li ha ensenyat una professora particular (es tracta d'una nena amb dificultats de tipologia "dislèxia"). El dibuix mostra una bona comprensió de la situació i li dic que molt bé (el seu treball serà un dels que triaré per comentar i veure que diuen els altres)

Reflexions al voltant del treball

- Els tiquets de compra, un document de càlcul de la nostra cultura
El treball a partir de documents reals, que la societat fa servir per a calcular, dóna al treball escolar la qualitat de la credibilitat, de que allò que fem realment serveix per a la vida, de que els serà útil als alumnes de portes enfora de l'escola. Sempre que treballem amb aquests documents (sigui el tiquet de la compra, la factura del preu de l'autocar per anar d'excursió, les taules de preus d'estada de l' hotel del viatge final d'estudis segons sigui temporada alta, baixa o mitja, etc.) l'interès dels nens i nenes està assegurat perquè l'activitat respon a la seva necessitat de comprendre el món adult. La classe de matemàtiques s'omple de sentit .

- L'ensenyament dels mecanismes de càlcul
Aprendre els mecanismes de les operacions ha representat tradicionalment el primer objectiu de la classe de matemàtiques, al qual hem dedicat tots els mestres la major part del temps i els esforços.
En canvi podem veure que dominar aquests mecanismes no assegura la comprensió de la relació entre les quantitats. Tampoc la pràctica continuada de càlculs d'aquests tipus representa una gran ajuda per al millorar les nostres estratègies de càlcul mental ni el nostre coneixement sobre les quantitats.
Els nens tenen moltes estratègies personals per poder resoldre situacions de càlcul que no deixen de sorprendre'ns. La pràctica d'aquestes estratègies sí que afavoreix l'evolució del pensament matemàtic dels nens i nenes, el càlcul mental, el seu concepte de quantitat, el domini del sistema de numeració, la confiança en ells mateixos.
Avui dia sembla massa agosarat prescindir de l'ensenyament del mecanismes però en el projecte de l'escola els retardem al màxim , ja que un cop han après el mecanisme els alumnes deixen de fer els seus càlculs personals que els suposem molt més esforç. Parafrasejant a l'assessor del nostre centre ,Carlos Gallego els algorismes van ser inventats per a que poguessin calcular les persones que no sabien matemàtiques.
Ara bé, és un aspecte que cal explicar molt als pares que de seguida detecten que el seu fill a 5è no sap dividir o a 3er no sap fer restes portant. A les reunions de pares ens fem un tip de fer-los resoldre situacions de dividir sense que puguin emprar el mecanisme, ho fem en grups perquè se sentin còmodes (no es tracta d'examinar a ningú) i sempre es generen discussions molt interessants. Poden vivenciar la presa de consciència dels elements matemàtics que els ha suposat aquest treball i comparar-lo amb el que hagués passat si haguessin fet la divisió. Si disposem de treballs de nens i nenes resolent aquest mateix problema es sorprenen i s'admiren del que són capaços de fer els seus fills. També és interessant fer-los pensar quantes vegades ells a la seva pròpia vida fan divisions per dues o tres xifres amb paper i llapis.

- L'ús de la calculadora
La calculadora és una eina de càlcul imprescindible avui dia a la nostra cultura. Als mestres ens fa de vegades una mica de por i restringim el seu us a situacions molt controlades. En aquest treball la calculadora va ser molt útil per a que tots poguessin tenir la satisfacció d'arribar a una solució, tot i que d'entrada els vaig demanar que intentessin resoldre el càlcul sense aquesta eina. La calculadora ens estalvia temps ( cosa que alguns càlculs llargs és necessari per no perdre'ns), ens estalvia esforços (ens permet centrar-nos en una dificultat com per exemple quants paquets d'agulles hem de comprar), ens dóna la seguretat de la comprovació o pistes sobre com deu fer per trobar aquest resultat.

- I ,com sempre...la diversitat a l'aula
Veient els treballs dels alumnes, escoltant el que diuen, sempre es manifesta una gran diversitat. Treballar de manera que tots aquests alumnes formin part activa de la comunitat d'aprenentatge de l'aula és un repte no gens fàcil d'aconseguir. D'altra banda no podem eliminar la diversitat: les solucions pedagògiques que no accepten aquest fet i intenten classificar als alumnes en grups homogenis , o treballar a l'aula per a un alumne "mig", inexistent no solucionen res perquè parteixen de la idea de que és possible igualar nivells i eliminar la diversitat.
En aquest grup d'alumnes hi ha molts que presenten dificultats per a les matemàtiques, alguns dificultats molt específiques (hi ha una nena diagnosticada de dislèxia que no sabem si algun cop podrà memoritzar les taules i no oblidar-les o entendre les relacions multiplicatives). Si la meva proposta fos tancada, si demanés a tothom el mateix, més de la meitat quedarien sense possibilitats de poder fer els exercicis i una gran part de la resta s'avorririen molt.
En canvi si la proposta és interessant i plena de sentit; si és oberta i deixo que cadascú faci servir les estratègies que vulgui (inclosos els dibuixos i l'ús de la calculadora) , si permeto que els nens s'ajudin , si respecto i m'interesso per les idees de tothom i aquest respecte passa a ser l'actitud habitual del grup... el miracle es produeix: tots treballen una proposta comú, el sentiment de pertinença a una comunitat d'aprenentatge es reforça, tothom rep el que necessita (els nens amb més bon nivell busquen normalment el "més difícil encara"; i els nens amb dificultats no es veuen marginats, comprenen el sentit del que fan i avancen).
Com a criteri de centre, no està previst que hi hagin organitzacions paral·leles al treball de l'aula ( del tipus de grup d'Educació Especial o Grup Flexible) . Es cert que hi ha algunes excepcions (alumnes que necessiten logopèdia o amb greus problemes de conducta) però sempre cal justificar el cas com una excepció a la regla i generar en aquell cas el tipus d'organització més pertinent segons les possibilitats.

Presentació de l'activitat (1ª part)

Es la tarda que havíem previst dedicar a fer les medalles. Tenim tots els materials necessaris a l'aula.
Comento als alumnes la necessitat de posar-nos d'acord sobre la grandaria de les medalles. Es una qüestió estètica, han de ser proporcionals a la cinta.
Mentre van passant els vuit metres de cinta, quatre blaus i quatre vermells perquè triin el color que els agrada, medeixin amb el regle els 28 cm i tallin un tros; els proposo de dibuixar en un full circumferències de diferents mides per veure quina queda millor. Els comento que per poder explicar com és la circumferència de la que parlin cal que apuntin la mida del radi cada cop, que medeixin la distància entre les puntes del compàs i un cop dibuixada assenyalin el centre i un radi i apuntin quant medeix .

Realització de l'activitat

Tenen poca experiència amb el compàs i la majoria no van gairebé (les potes s'obren amb facilitat). Malgrat tot tots treballen amb interès, s'ajuden i es deixen el compàs si hi ha un que va malament. Veig que apunten sense dificultat els radis. La majoria opten per nombres enters (2, 3, 4 cm), alguns es decideixen pels decimals (2,3; 2,9; 2,5). En aquest últim cas no tenen cap dificultat en expressar les unitats mm del regle en forma de decimal de cm.
Al mateix temps van passant les cintes i tallen 28 cm sense cap mena de problema.

Segona part del treball

Tots tenen les cintes tallades i les circumferències dibuixades. Van provant amb la cinta la mida que els sembla millor i fem una votació.

Nen per nen em diuen la mida que volen. Jo "forço" que surti la paraula radi.
Nen/a- "Dos cm
Mestra-"Dos cm de què"
Nen/a- "De radi"
Vull que vegin que per mi és important que diguin aquesta paraula, però és veritat que resulta forçat repetir-la tants cops.
La circumferència més votada va ser la de 3 cm de radi.
Així doncs passem a fer les medalles d'aquesta mida. Cadascú triarà el color de cartolina que li sembli millor i un cop feta la rodona , farà un avió de la manera que vulgui i l'enganxarà a dins (els nens de cinc anys són la classe dels avions i per això ja havíem parlat de que en comptes d'un animal ,com en el llibre del model, els faríem un avió)
Quina meravella d'avions! De tota mena, de tots colors, un de mòbil (penjant d'un fil), un en 3d... (podeu mirar les fotografies).
Encara queda un problema a resoldre i és que hem de fer 26 medalles i només som 21 nens avuí a la classe. Decideixen voluntariament quins cinc alumnes faran dues medalles.
Només queda enganxar-les a la cinta, enganxar la cinta doblegada i passar l'agulla imperdible.
Les anem posant a una caixa en exposició i ens sentim molt orgullosos del resultat. Segur que als nostres companys de 5 anys els agradaran molt aquestes medalles!

Reflexions sobre l'activitat

Continguts matemàtics importants van ser treballats durant la tarda:
. experiències de mesura de longituds: us d'eines (regle, compàs) , us d'unitats de mesura, els cm
. experiències de numeració: els nombres decimals (2,5 ; 2,9 cm, per exemple) ,
.experiències de geometria:les circumferències, el disseny dels avions (2d, 3d), la proporcionalitat entre les parts de l'objecte medalles (cinta, rodona, avió).

Però la manera de treballar aquests continguts: dintre d'un context, com a resposta a unes necessitats d'una activitat no matemàtica sino real i per tan global , fa que aquests continguts s'omplin de significat i que el cervell els classifiqui com a "útils a llarg termini, necessaris per la vida" i no els oblidi amb facilitat.

Treballar d'aquesta manera és més lent però els aprenentatges són més ferms.
Treballar d'aquesta manera vol dir que els continguts no segueixen un ordre imposat per l'assignarura però els continguts importants surten tots. Cal que els mestres tinguem uns bons criteris per dedicar el temps al que és prioritari. Amb l'experiència cada cop sabem més del tipus d'activitats que porten a uns continguts o a uns altres. Al principi nosaltres som els primers sorpresos i prenem consciència de la utilitat de conceptes que hem aprés de manera teòrica pel tipus de formació que hem rebut.

Presentació i desenvolupament de l'activitat

Recordo als alumnes que el dia anterior havíem estat dibuixant circumferències de diferents mides per decidir la mida de les medalles.
-Mestra-"Recordeu de quina mida les vàrem fer?"
-Nens- "De tres cm de radi"
-Mestra- "Avuí estudiarem quines altres línies i figures de la circumferència i el cercle, a part del radi, ens pot interessar aprendre. Les anirem dibuixant a la pissarra i tots les fareu al vostre full. Començarem fent una circumferència amb el compàs i dibuixarem radis diferents" (Jo faig una circumferència a la pissarra i surten quatre alumnes a dibuixar quatre radis, parel.lelament ho van fent a les fitxes que hem repartit)
Veig que no els resulta fàcil dibuixar circumferències amb el compàs, no hi estan acostumats i els compassos no són gaire bons. Representar els radis ho fan sense dificultat.
-Mestra- "A part del radi els matemàtics han definit altres línies interessants en una circumferència, als diferents llibres de text de la classe les podem trobar a les lliçons que parlen de la circumferència i el cercle.
Una és el diàmetre. Si aneu a comprar una mànega , un tub o una anella; el radi no ens serveix massa perquè no sabem on és el centre, la mida ens la dòna el diàmetre, de banda a banda la distància més gran (dibuixo una altra circumferència a la pissarra i faig un diàmetre). Al paleta li diran al magatzem de material: vol la tuberia de 10 cm de diàmetre , o de 12...?
El diàmetre també passa pel centre i val el mateix que dos radis, veieu cada diàmetre té dos radis, un a cada costat del centre"
Surten més alumnes a la pissarra a dibuixar altres diàmetres i tots ho van fent al full.
-Mestra.- " Si agafo la meitat d'una circumferència, d'aquesta línia els matemàtics en diuen semicircèmferència, semi vol dir meitat. Per pintar una semicircunferència justa heu de dibuixar un diàmetre, que la parteix en dos trossos iguals. Surten dos semicircumferències"
-Mestra.- "Encara hi ha més línies interessants, mireu aquesta uneix dos punts però no passa pel centre, és una corda. La corda és molt interessant perquè ens permet trobar el centre de qualsevol circumferència, un dia ho farem."
Surten alumnes a dibuixar cordes diferents i van fent tots la fitxa
-Mestra.- "Les línies que hem dibuixat eren a partir de circumferències. Ara representarem línies i figures a partir d'una altra cosa diferent , que és el cercle. Qui vol explicar quina diferència hi ha entre un cercle i una circumferència?"
-Nen.- "El cercle està ple i la circumferència està buida"
-Mestra.- "Molt bé. Algu vol dir més coses"
-Nen.- "La circumferència és lo de fora i el cercle lo de dins"
-Mestra.- "Molt bé: la circumferència és una línia, només té una dimensió; en canvi el cercle és una figura plana, té dues dimensions.
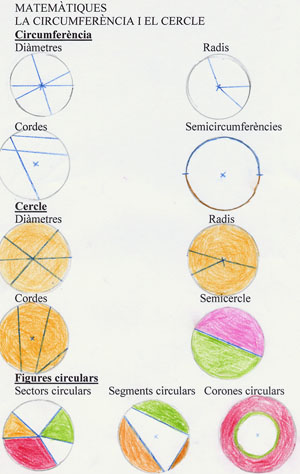
Continuem l'activitat de manera similar i dibuixem els radis i diàmetres del cercle, sectors circulars, segments, corones i semicercles.
Els pregunto si ells han fet servir o han vist alguna vegada aquelles figures en les representacións gràfiques.
Em diuen que sí els sectors i les corones les han fet servir al racò de periodistes per representar els tants per cents. Jo els dic que tenen raó i els vaig recordar una representació d'un nen que s'havia inventat fer-ho amb segments circulars (s'imaginava el cercle com si s'anès omplint , el nivell pujava com si fos un líquid i el 90% era gairebé tot ple). Era cert però que la manera convencional de representar els percentatges era mitjançant sectors o corones circulars
A la cartellera de racons encara tenim penjada la representació gràfica que va fer un alumne del resultat d'una enquesta , realitzada en el marc del racó de periodistes

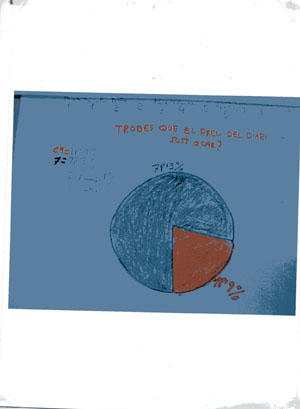
Els alumnes responsables de les cartelleres s'encarregaran d'escriure al mural de matemàtiques tots aquests conceptes que avuí hem treballat.

Reflexions sobre l'activitat

- Context i currículum

Amb la nostra manera de treballar procurem que els continguts sorgeixin com una necessitat, dintre d'un context que faciliti als alumnes la comprensió del seu significat. Els continguts s'aborden des d'una óptica globalitzada sense seguir les assignatures de forma parcialitzada. En aquest cas havíem arribat a la necessitat de definir el radi de les circumferències per poder-nos comunicar de quina mida faríem les medalles i que totes fossin igual de grans. Es com si els continguts matemàtics els segmentéssim i els treballéssim dins d'organitzacions diferents: als racons, als tallers de preparació de festes, a les activitats d'organització de la vida quotidiana.
Però després cal organitzar aquest puzzle, cal arribar a les matemàtiques com a ciència molt important dins de la nostra cultura, amb uns continguts específics , organitzats amb una lògica que parteix de la pròpia materia i que ja no tenen a veure amb situacions concretes.
Poder compaginar les dues visions és difícil. Com a mestres hem anat seguint una evolució. Ara mantenim una doble organització a l'aula. Per una banda els continguts parteixen de situacions globalitzades i els treballs s'arxiven segons els criteris: festes, racons, projectes, organització d'aula, etc. Per altra banda els continguts es treballen dins d'altres situacions hipotètiques, ja no lligades directament a les vivències dels nens i nenes, també s'amplien o s'organitzen , consultem els llibres de text, els pengem al mural de les matemàtiques. Els nens fan servir un altre tipus d'arxiu on aquests treballs no lligats directament a les necessitats de l'aula s'organitzen segons les àrees curriculars: matemàtiques, llengua, ciències naturals, ciències socials...Sempre és un equilibri difícil, sovint provoca el debat entre els membres del Claustre, i es que tot és important però el temps és limitat.
Els continguts apareixen o s'aprofundeixen i s'organitzen més lentament que si eliminéssim el context però dificilment s'obliden, la xarxa que es genera a la ment dels alumnes es mostra molt més sòlida i potent que en la realització de tasques escolars tradicionals.
Per completar aquesta visió de la problemàtica cal esmentar l'actitud de tranquil.litat dels pares quan veuen treballs de sistematització i en canvi el neguit que mostren davant els treballs globalitzats i les preocupacions que expressen sobre si estaràn ben preparats quan passin a l'institut (sobretot al cicle superior) . Molt sovint necessitem fer reunions d'aula per explicar el treball que estem fent i contenir les pors de les famílies perquè no perdin la confiança en l'escola.

- Propostes tancades. Activitats dirigides

Quan estem acostumats a donar als alumnes un full en blanc per què resolguin un problema, ens dònin les seves opinions, organitzin propostes i itineraris de treball; quan preferim treballar documents reals, propis de la cultura i del món adult...un tipus de treball com aquest sempre resulta molt pobre. Una activitat dirigida que ens dòna molt poca informació sobre el pensament dels nens i nenes. Als mestres ens assalten dubtes sobre l'aprenentatge real que produeixen aquest tipus de tasques.
Representen una mínima part del treball a les aules i responen a les necessitats d'organitzar l'assignatura, de que cada alumne tingui al seu dossier el que anem organitzant al mural de la paret, de conectar amb les famílies i amb el treball que realitzen altres escoles...Segurament l'experiència ens ajudarà a tenir criteris més clars sobre el valor d'aquest tipus de tasques.

- El mestre, dissenyador i editor dels treballs escolars

Al centre hi ha un punt de concentració, nervis, cues...:la sala de màquines. Si la fotocopiadora s'espatlla, o la màquina de ciclostil, es produeix una crisi important.
És un dels punts febles. El mestre necessita dedicar moltes hores a preparar aquestes fitxes i a imprimir-les.
L'ordinador és un gran ajut (aixì com la càmera digital) però , fins que no té un cert domini, requereix també molt temps. De vegades el resultat no és massa estètic o poden haver errors.
Els pares ens diuen que el món és en colors però el cost d'imprimir en color no ens el podem permetre...
Tot i que és un problema organitzatiu, no pedagògic em sembla important tenir-lo present perque pot arribar a fer inviable l'escola pel temps que demana del mestre.
Hauríem de poder utilitzar materiars ja editats en certs moments que ens estalviessin feina. El problema és que costa molt trobar aquest tipus de materials, ja que les nostres necessitats són molt minoritàries. Els llibres de text i quaderns d'exercicis tenen altres funcions i estan fets sota altres criteris. Tot i així de vegades els utilitzen com a recurs per omplir aquest buit.
Treballar d'aquesta manera fa necessari disposar de molts materials (atles, enciclopèdies, projector de cossos opacs...) que enriqueixin i afavoreixin les experiències d'aprenentatge dels alumnes. La gestió econòmica del centre ho ha de tenir molt present.

1. Proposta als alumnes

Ahir vàrem estar consultant als llibres de text les lliçons que parlaven de la circumferència i el cercle .
Vàreu dibuixar als vostres fulls, diàmetres, cordes, semicercles i altres línies i figures circulars.
Els llibres de 5è també diuen que la longitud de la circumferència és tres vegades el diàmetre aproximadament, una mica més de tres diàmetres. Ho comprovarem mesurant les circumferències que trobem als objectes de la classe.
(Amb l'ajut d'un cordill mesurem la longitud de les circumferències mínima i màxima de la paperera, després la tapa d'un pot.)
Uns alumnes comenten que no entenen com sempre és el mateix, tres diàmetres i una mica, que si la circumferència es més gran hauria de donar més... La resta no ho veuen clar. Jo els dic que això passa perquè també és més gran el diàmetre i la relació és la mateixa sempre com hem vist : tres diàmetres i una mica, i continuo.
"Des de l'antiguitat els homes ja havien descobert que la longitud de qualsevol circumferència era 3 diàmetres i una mica més.
Ara us explicaré la història de com els matemàtics van estar buscant durant molts anys el valor d'aquesta mica més. Volien trobar la fórmula de la longitud de la circumferència, i per això volien saber per quin número calia multiplicar el diàmetre més exactament (si multiplicaven per tres s'aproximaven però la circumferència en realitat era més llarga , calia multiplicar per un número una mica més gran de tres). Ja veureu que els va costar molt, varen trigar segles.
Serà com una conferència. Podeu prendre els apunts que volgueu. Jo porto algunes dades apuntades perquè no me les sé de memòria (els ensenyo el paper), les he trobat a les enciclopèdies, algunes també us les apuntaré a la pissarra però no cal que les copieu si no voleu: només apunteu el que considereu més important. Després haureu de fer un resum.

Desenvolupament de la "conferencia".

"A l'antiga Grècia els matemàtics volien saber el valor d'aquest tros que sobrava. Intentaven aproximar-se però no ho aconseguien. Van decidir que a aquest número que era una mica més gran de 3 però no sabien exactament quant era li posarien el nom d'una lletra, el nom d'una lletra grega, Pi, que s'escriu d'aquesta manera, ? . Així ja podien escriure que la fòrmula de la longitud de la circumferència era:
l = d x ? (escric la fòrmula a la pissarra)
Però continuaven sense saber quant valia Pi.
El que més es va acostar a l'antiguitat va ser Arquímedes de Siracusa. Siracusa és una ciutat de l'illa de Sicília, que està al sud d'Itàlia."

Alguns nens comenten que tenia un nom ben estrany, altres diuen que lleig. Jo els dic que en aquella época potser dir-se Arquímedes era tan normal com ara dir-se Pol o David.

"Arquímedes va nèixer l'any 287 a JC i va morir l'any 212 a JC" (escric els anys a la pissarra)

Hi ha una protesta general. Diuen que no pot ser.
Jo dibuixo a la pissarra una recta i represento on serien alguns anys amb el seu ajut. Representem el 0 a la recta com el moment en que va néixer Jesús. Els pregunto què vol dir abans de Jesucrist. Tots estan d'acord que són anys a l'esquerra de la recta. Situem alguns anys a JC:, 5, 10, 100... i al final el 287 i el 212.
Alguns diuen que sí que pot ser. Un nen diu que els anys a JC són com els nombres negatius.
Abans de seguir amb la història els comento que la nostra cultura compta els anys a partir del naixement de Jesucrist però d'altres pobles ho fan a partir d'altres fets i per a ells no és l'any 2003. Per exemple, els xinesos, els àrabs... Li pregunto a uns nena magribina de la classe si sap en quin any estan les persones de la cultura àrab i no ho sap però quedem que ho preguntarà a casa i ens ho dirà.

"El pare d'Arquímedes era astrònom. De ben petit Arquímedes veia al seu pare fer càlculs molt difícils per saber el moviment i la distància dels astres i ell va voler ser matemàtic i ara se'l considera el matemàtic més important de l'Edat Antiga. Va llegir tot el que havíen escrit els matemàtics grecs sobre el número Pi i ell va continuar investigant sobre quin era el seu valor. Va arribar a aproximar-se molt". (Escric a la pissarra les dades numèriques)

3 + 10/71 < ? < 3 + 10/70

" Arquimedes ho devia escriure amb números romans, perquè en aquella epòca eren els romans qui havien conquerit Sicília i encara no utilitzaven els nostres números, que els van portar els àrabs més tard. Arquímedes, no coneixia el sistema de numeració decimal, no podia escriure el número ? amb nombres decimals, com nosaltres ho faríem ara, 3,..,. Només ho podia fer en forma de fraccions."

Comentem l'expressió numérica de la pissarra. Hi ha nens que diuen que 10/71 és més gran que 10/70, per la qual cosa l'expressió és impossible.
Pregunto si tothom està d'acord i hi ha diverses opinions. Jo faig referència a una altra discusió que s'havia produït a l'aula dies enrerra: què era més ½ o 1/3. Llavors ho haviem estat comprovant amb dibuixos i valors numèrics. "Si d'una cosa faig 70 trossos, i d'una altra igual faig 71 trossos, quins trossos seràn més petits?"
(Crec que ho comprenen parcialment però no insisteixo i continuo la història)

"Arquímedes va ser mort per un soldat romà, segurament va ser una confusió perquè el cònsul romà l'apreciava molt. Diuen que potser el soldat li va dir alguna cosa i ell no se'n va adonar, concentrat com estava en els seus càlculs...no se sap ben bé què va passar.
Van passar els anys i els segles i no hi havia manera de trobar quin era exactament el valor de Pi.
A partir de l'Edat Mitjana els càlculs es feien ja amb el nostre sistema de numeració decimal (l'havien introduït els àrabs). Els matemàtics utilitzaven els números decimals per arribar al valor de Pi, cada vegada s'aproximaven més: ? = 3,141592653589...(escric el número a la pissarra fent una pausa entre l'escriptura de cada xifra decimal) però sempre, quan multiplicaven pel diàmetre faltava un tros per arribar a la longitud de la circumferència, malgrat s'aproximaven cada cop més."

Dibuixo a la pissarra la recta numèrica i situo les unitats del 0 al 5 , els pregunto on situarien el número que acabo d'escriure a la pissarra. Davant la meva sorpresa no tenen cap dubta, va entre el 3 i el 4. De seguida veig que he donat massa pistes.

"Els matemàtics van començar a pensar que potser Pi no donaria mai exacte, que potser no es podia calcular però no ho sabien.
Va ser al segle XVIII, quan un altre matemàtic, Jean-Henri Lambert va demostrar que Pi era un nombre irracional, que no es pot calcular, mai dòna exacte. Lambert va viure entre 1728 i 1777 a França i Alemanya.
Al segle XX amb un potent ordinador IBM es van arribar a calcular els primers 100.000 decimals de Pi, però no dona mai exacte perquè és un nombre irracional com va demostrar Lambert"

La història s'ha acabat i han estat molt interessats tots. (a l'endemà un nen em diu que quan tingui un fill li posarà Arquímedes de nom)

Els dic que haurem d'afegir al mural de les fòrmules la de la longitud de la circumferència i al dels nombres, els nombres irracionals, que potser en trobarem més ara només sabem el número Pi. Un alumne diu , segur que hi ha molts, un altre afegeix hi ha infinits!.

Reflexions sobre l'activitat"

Jo m'havia proposat dos objectius ben diferents:
El primer fer viure als nens i nenes la matemàtica com a part de la cultura i la història dels homes. Apropar-los als matemàtics, al valor del pensament matemàtic, de la curiositat intel.lectual.
També volia ampliar la seva visió sobre els nombres, acostar-los a la idea de l'infinit que hi ha entre dos decimals, introduir la idea de nombre irracional.
Els continguts eren complexes. Els nens capten que allò que expliques és de debò i els interessa molt més que si ho simplifiquem tot pensant que no ho entendran. Cada nen i nena entén segons les seves capacitats i experiències però tots entenen alguna cosa i ningú ho entén tot. Es tracta de continguts importants, ja ens els tornarem a trobar aquest curs, o a 6è o a l'ESO i seguiran avançant. Crec que és l'única manera de poder treballar en la diversitat. Durant la sessió hi havia present una companya i em va comentar que li havia sorprés la cara d'atenció i plaer de tots ( és un grup d'alumnes molt mogut i de vegades costa aconseguir un bon ambient de treball a l'aula).

Durant la sessió es produí un debat que jo no havia previst sobre temes interessants (anys a JC, comparació de fraccions, els noms de la gent...), aspectes proposats pels propis alumnes que , només per aquest fet, són poderosos a l'hora de aprofundir en els coneixements.

La modalitat de treball :"conferència" em sembla que aporta valors interessants, hi és present a la cultura com a forma de transmissió de coneixements, crec que ha de ser present a les aules i ,si és possible, donada per un expert. La llibertat donada als alumnes per prendre els apunts que considerin importants em sembla que afavoreix molt la seva capacitat de valorar el que se'ls diu. De fet els alumnes em sorprenen quan sistemàticament valoren el que els dic i ho qüestionen si no ho veuen clar.

Hi ha un altre aspecte problemàtic, relacionat amb la constatació anterior : quan hem de donar la solució els mestres?. Ara ja sabem que donar la resposta no vol dir que els alumnes la facin seva i que si sempre donem la resposta els alumnes deixen de pensar. Però si que cal de vegades aportar algunes dades, crec que pot ajudar sovint a la dinàmica de l'aula i que si ho fem d'una forma equilibrada no és contraproduent. Durant la sessió els nens no veuen que la raó entre el diàmetre i la longitud de la circumferència és constant, potser no és el moment per a molts i ara no m'interessa dedicar el temps a discutir aquest tema, per això faig la meva aportació i continuem. Sòc conscient de que la majoria no han entés del tot el que he dit però sempre penso que alguna cosa comencen a entendre...
Quan gestionem l'aula prenem constantment decisions, seguim uns camins i en deixem uns altres ja que és impossible fer-ho tot. De vegades ens equivoquem i a mida que ens fem més experts veiem que podíem haver seguit un altra via més profitosa però crec que la majoria de vegades el resultat es positiu. Per sort els continguts importants ens els trobem a cada moment i hi ha moltes ocasions per seguir aprofundint.

- Els apunts que van prendre els nens i nenes:
La major part dels apunts són la còpia del que jo anava apuntant a la pissarra però gairebé totes les còpies són diferents ja que decideixen apuntar unes coses o unes altres.
Només en el cas d'una alumna veig frases estil telegrama "matemàtics preocupats", "àrabs van portar nºs decimals"; que acompanyen el que ha copiat. Crec que el temps ha estat un factor important: si jo escrivia ells podien copiar però si jo parlava havíen d'anar molt més ràpidament i no només per escriure sinò també per a prendre les decisions i seguir escoltant.
La mateixa nena representa gràficament l'enunciat del problema que ens ocupa: trobar la fòrmula de la longitud de la circumferència .

- Els resums:
Hi ha una gran diversitat de produccions. Des de nens i nenes que expliquen la història gairebé en la seva totalitat a alguns que només escriuen un parell de frases. En alguns casos donen més importància als aspectes personals, en d'altres a les qüestions científiques. No falten errors com dir que Siracusa era un matemàtic o que Lambert va inventar els nºs decimals però tots crec que han pensat en que hi havia un problema matemàtic a resoldre, que era difícil i va costar molt de temps arribar a la solucions i que al llarg de la història els matemàtics s'hi anaven aproximant.

En aquest cas hi ha dos finals. El primer el podeu veure a les fotos: l’entrega dels regals a la classe dels avions. Els van encantar les medalles , la Joana, la seva mestra els va dir que era una medalla de pilot i els nens de 5è els van ajudar a posar-se-les. Era l’ultim dia d’escola i tot seguit sortíem al carrer a cantar nadales, podrien lluir la medalla i tothom la veuria.

Els de 5è , alumnes i mestres (ja que a part de la tutora, la Loli, mestra de suport , ens havia acompanyat i ajudat durant gran part del procés) estàvem molt satisfets, contents i emocionats.

El segon final va ser a la reunió amb els pares i mares de l’aula que es va fer la darrera setmana del primer trimestre. Un tema de l’ordre del dia , a petició de les famílies era el treball dels continguts del currículum.

Vaig aprofitar el recull de materials de que disposava de la història de les medalles per presentar-la als pares i tots van dir que els va agradar molt i els va ajudar a comprendre com treballaven, ja que alguns van confesar les seves preocupacions en veure ja a prop l’entrada a l’institut.

Són les vacances de Nadal. Quan tornem a l’escola haurem de començar a pensar en la Festa Major i el Carnaval!

1.-La història de les medalles continua...

La història de les medalles ens va permetre treballar a la classe una gran quantitat de continguts matemàtics. La majoria d’aquests continguts no eren nous per als nens i nenes que ja havien tingut moltes experiències anteriors de resolució de problemes sobre preus i costos (estratègies de càlcul, decimals, arrodoniments, lectura de documents...), de reflexions sobre el Sistema de numeració (trencats i decimals), de mesura (magnituds: longitud, 1Di 2D, us d’eines, unitats: m i cm), d’àlgebra (escriptura de fórmules), de disseny (funcionalitat i estètica , proporcionalitat, figures geomètriques).

Cada nen i cada nena tenien ja moltes idees, idees que van evolucionant constantment amb les seves vivències dins i fora de l’aula. Segurament alguns coneixements eren nous per a ells (nombre irracional, la longitud de la circumferència) i cada alumne els va poder veure “a la llum” del que ja sabia i va buscar a quin lloc de la xarxa dels seus coneixements els podia connectar.

Segurament tot el que va passar a l’aula durant aquestes sessions va servir per què cada nen i cada nena establís nous lligams i reforcés les connexions d’aquesta xarxa de coneixements pròpia.

El grup, com a comunitat d’aprenentatge, va permetre transcendir aquest nivell individual a l’haver de construir conjuntament acords, validacions; a l’ exigir de tots una comunicació coherent i comprensible, al fer-se dipositari dels nous coneixements que anaven apareixent i s’anaven materialitzant (mural de matemàtiques).

Després de les vacances de Nadal , en ocasions molt diverses vàrem haver de fer referència a la història de les medalles. Les diferents situacions que se’ns van presentar van permetre posar en joc els mateixos continguts des d’altres punts de vista, en situacions ben diferents, amb un major grau d’aprofundiment.

Faig referència a algunes d’aquestes situacions. He seleccionat les experiències relacionades amb la circumferència i el cercle, ja que és impossible explicar-les totes:

a) La maqueta del Sistema Solar (Racó d’arquitectura )

Una nena a la “ rodona de racons” (espai horari on cada alumne explica el seu treball un cop finalitzades les dues sessions de racons) ens explica que s’havia proposat fer una maqueta del Sistema solar. La volia posar dins una caixa quadrada i per això va desestimar representar les distàncies de manera proporcional. Només representaria l’ordre dels planetes i les seves òrbites . Les òrbites les faria circulars, separades per dos cm l’una de l’altra.
Ens diu que, un cop tallats, doblegats i lligats els filferros que representen les diferents òrbites, veu que no ha aconsegueix el seu propòsit (que estiguin separades per 2 cm).
El grup, amb la maqueta al davant, li pregunta com ho va fer. S’explica malament i entenem (tots!) que ha tallat els diferents filferros cadascun 2 cm més llarg que l’anterior.
La meva primera sorpresa és que ningú protesta, totes les intervencions són sobre si no havia controlat el tros de filferro sobrant per lligar els dos extrems!
Aquest fet em va fer pensar molt. La fórmula de longitud de la circumferència (que tenim penjada al mural), explicada com una conferència no els serveix per resoldre aquest problema pràctic, no hi veuen cap relació. Penso aprofitar aquesta oportunitat i dedicar l’endemà una bona estona a resoldre el problema de les òrbites i així ho apuntem com a tasca pendent.
Al dia següent iniciem el matí parlant de les òrbites en gran grup. Faig dibuixar a l’alumna el seu projecte a la pissarra. Veig que els resulta molt difícil i decideixo intervenir per simplificar la situació. Faig que l’alumna decideixi el valor del radi de la primera òrbita i, a partir d’aquí va dibuixant.
Mestra.- “Si el radi de la primera circumferència és 3 cm, quant valdrà el radi de la segona òrbita?” El dibuix ajuda molt. Molts veuen clarament que són dos cm més i així anem calculant els radis de totes les òrbites.
Mestra.- Bé, ara hem de saber quant filferro necessitem per fer cada circumferència, com ho podem calcular?...(silenci)... ens pot servir la longitud dels diferents radis? Ningú respon.
Mestra.- Recordeu que quan vam fer les medalles per als Avions vàrem parlar de com es calculava la longitud de la circumferència?
La majoria sap on tenim la fórmula penjada malgrat fins ara no l’havíem feta servir.: Longitud de la circumferència = d x ?
La majoria diuen que el diàmetre és dos radis. El problema es planteja amb multiplicar per ?. Mestra.- Si ? és irracional, no pot ser mai exacte, cada cop hem de decidir quant d’exacte volem que sigui el nostre càlcul, segons la situació desestimarem més o menys decimals. En aquest cas, si calculem en cm el primer decimal seran els mm i ja no tenim unitats més petites al regle...Què us sembla?
Un nen diu que 3.1 és molt poc aproximat. Davant la meva sorpresa decideixen multiplicar per 3.14, i després arrodonir.
Tots fan els càlculs al seu full, nou cops (un per planeta) han d’aplicar la fórmula, i després afegir 2 cm per poder lligar els extrems. Els proposo calcular amb calculadora per anar més ràpids.

Els proposo penjar la fórmula al Racó d’Arquitectura per si algun dia la tornen a necessitar. Acompanyarem la fórmula amb la foto de les òrbites i així ho recordarem.

Com anècdota: en acabar els càlculs, l’autora de la maqueta em diu secretament que no l’havíem entès, que ella en realitat anava fent les òrbites donant-les forma sobre del regle, directament, mirant que quedessin separades per 2cm (“anava fent els filferros cada cop 2 cm més”) . Jo li dic que veig que sabia molt bé el que es feia, que això era més lògic que no tal com ho havíem entès. Ho expliquem al grup sense donar més importància, i jo comento que aquesta situació havia estat molt interessant perquè ens havia permès aprendre més coses de la circumferència.

Reflexions

Aquesta nova situació sobre el coneixement del càlcul de la longitud de la circumferència és completament diferent a la que es va produir a la “història de les medalles”. Ara es tracta d’una situació instrumental , hem de solucionar un problema pràctic. Anteriorment havíem abordat aquesta qüestió des de la història de les matemàtiques i com un contingut que apareixia al llibre de text. Hem vist com els alumnes tenen de vegades dificultats per reconèixer el contingut après en situacions i contextos diferents.
Per això cada nova situació aporta nous valors i quan més variades siguin aquestes situacions més rica serà la experiència dels alumnes i més profunds els coneixements.

En el cas de la longitud de la circumferència l’aprenentatge no s’enriqueix de manera quantitativa , no sap més coses sobre la longitud de la circumferència. L’aprofundiment que se’n fa és ,podríem dir, qualitatiu. Per a què pot servir saber calcular la longitud de la circumferència? La situació real amb la que ens vàrem trobar ens va aportar la força de la necessitat. Segurament hagués estat diferent si la proposta hagués partit d’una situació simulada.

En canvi si que apareix la necessitat d’aprofundir sobre què representa un nombre irracional a l’haver d’operar amb ell, la qual cosa augmenta la quantitat de contingut a la que exposem als alumnes.

b) El rellotge de sol (Racó d’experimentació)

Dos nens ens mostren a la rodona de racons el rellotge de sol que han fet. Diuen que no es van decidir fins molt tard sobre quin projecte dur a terme i per això les parts les van fer molt ràpidament i són desiguals. També diuen que no van tenir temps d’acabar de posar les hores (vegeu la imatge del costat)
Després de discutir sobre si els rellotges de sol són així (el model utilitzat és com el rellotge d’agulles amb un pal clavat) i com es pot fer un rellotge de sol, passem a parlar sobre com es pot partir un cercle en parts iguals.

Anem a buscar els transportadors al racó d’Arquitectura i parlem de graus. Els dic que el cercle complet té 360 i practiquem una bona estona partint diferents cercles en 3, 4, 6, 10, 12 parts. Pengem la informació a la cartellera i fem una còpia per al Racó d’Arquitectura.

Reflexions

En aquest cas hem pogut ampliar el que sabíem sobre el cercle i la circumferència. Aquest mateix problema va aparèixer a finals de curs. Els alumnes havien inventat preguntes d’història per construir un joc del tipus “Trivial” . Van voler comprar les fitxes de joc al mercat (formatgets) però no les venien sense el joc. Llavors van decidir que dibuixarien els cercles dividits en sis parts i cada jugador aniria pintant cada part del color corresponent a mesura que anés guanyant Una parella es va encarregar de fer el dibuix dels cercles partits ,que després fotocopiaríem i, ho van fer molt bé amb el transportador de manera completament autònoma. Quan ens ho van ensenyar vam aprofitar per que ens recordessin com es feia.

c) La disfressa de hawaians i hawaianes (Taller de Carnaval)

En aquest cas ens havíem confegit la disfressa amb flors de paper de seda i fil elàstic. Les flors les formàvem a partir de cercles que havíem dibuixat amb plantilles i retallat Per elaborar el dossier vàrem voler apuntar com havíem fet la disfressa i no sabíem com posar la mida dels cercles, ja que a l’estar fets amb plantilles (tapes i pots) no sabíem quin era el radi ni quin era el centre.
A partir d’aquí vam aprendre a buscar el centre d’un cercle. Primer a partir de les idees dels propis alumnes (algunes molt encertades com doblegant el cercle de paper de seda) i després com ho feien els matemàtics: traçant la mediatriu d’una corda.

Reflexions

En aquest cas, vàrem seguir aprofundint els coneixements sobre la circumferència i el cercle a partir de la Festa de Carnaval. Si busquéssim al llibre de 5è informació sobre com trobar el centre a partir d’una corda, no la trobaríem ja que la distribució de continguts la reserva per bastant més endavant. En canvi no va ser gens difícil i sobretot va valer la pena introduir aquest contingut en uns moment ple de significat per a ells.

d) El sostre dels túnels (Racó d’Arquitectura)

Tres nens venen del racó d’Arquitectura amb una maqueta sense acabar, han retallat dos rectangles de cartolina per a fer el sostre, han pres les mides directament, fent coincidir la cartolina amb el semicercle del túnel . Plantejo als alumnes que si la maqueta fos més gran o fos una construcció real no es podria fer aquesta manipulació directa. Com es podria fer? Abans els autors ens mostren la forma rectangular dels dos sostres i com encaixen a l’estructura dels ponts. Deixem la maqueta al centre de l’aula per a que puguin mirar-la i prendre les mides que vulguin.
Treballen individualment, sabent que després en farem un debat.
D’entre tots els treballs he seleccionat dos ben diferents com a representació de la diversitat de l’aula.

La primera alumna mostra una comprensió molt bona del problema, dissenya un pla on totes les accions tenen sentit, no pren cap mida innecessària, no necessita fer cap dibuix per visualitzar la situació, només pinta a la fotografia les dimensions que són significatives en aquest cas.

Ben diferent és el segon exemple.

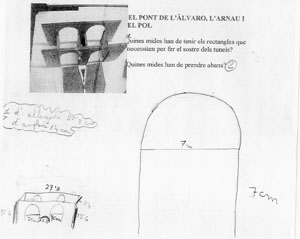
No ha pogut visualitzar la transformació de les voltes en rectangles i, com que demanem les mesures d’aquests rectangles, pensa en un rectangle pla que cobreixi tota l’estructura. I aquestes són les mides que dóna com a solució , destacada en el núvol.

Arribar a aquesta solució no li ha estat fàcil. Crec que per això espontàniament té la necessitat de dibuixar la situació, i comença prenent moltes mides sense saber ben bé què en farà.

Reflexions

No sabem si la nena del segon exemple després del debat es va adonar de que aquest no era el rectangle que es demanava i fins a quin punt va poder visualitzar com a rectangles les voltes dels dos túnels. Els mestres mai controlem els processos íntims d’aprenentatge significatiu que es produeixen en el cap dels nostres alumnes, depenen de moltes variables que no podem controlar. Malgrat aquest fet l’aprenentatge es produeix, el grup avança, avancen els alumnes, tots els alumnes (encara que en moments i ritmes diferents). També és cert que si bé no controlem sí que influïm de manera molt decisiva en aquests processos.

Les estratègies per resoldre els problemes, si deixem llibertat als nens i nenes, resulten sempre molt “econòmiques”: cadascú fa allò que necessita fer. Si no comprèn la situació la dibuixarà, si no necessita dibuixar s’estalviarà aquesta feina. Són ells qui porten el control, qui prenen les decisions.
Cada treball ens permetrà acostar-nos molt al pensament del seu autor. Els resultats seran molt diversos i creatius.
De vegades els mestres hem cregut que sistematitzar la manera de resoldre els problemes ajuda als nens i els obliguem a seguir tot un procés (dades, dibuix, operacions, solució, comprovació, resposta...) i /o a distribuir l’espai d’una determinada manera. Des del meu punt de vista no és necessari , resta espontaneïtat i creativitat, i no aporta valors a la confiança dels alumnes en ells mateixos ni al treball en la diversitat.

TEIXINT EL CURRÍCULUM

Moltes altres situacions, al llarg del curs, varen ser viscudes a la classe provocant la necessitat de recórrer als continguts treballats a “la història de les medalles”. És impossible explicar-les totes. Molts cops calia ampliar el que ja havíem treballat, altres simplement calia ampliar la perspectiva sobre aquests continguts al canviar el context o tipus de situació.
Poc a poc el currículum va prenent forma, es va materialitzant. Els coneixements dels nens i nenes formen una xarxa cada cop més atapeïda i més connectada, i així seguirà al llarg de tota la seva escolaritat i tota la seva vida.
La història de les medalles no tindria sentit si no és vista des d’aquesta posició ,dins d’un continuum que no s’acaba mai.

Sempre els mestres ens preocupem pels continguts del currículum:
Si no seguim la pauta que ens marca el llibre de text com ens podem assegurar de que els alumnes sabran tot el que han de saber?.
Si la nostra dinàmica respon a les necessitats que moltes vegades són plantejades pels mateixos nens i nenes, les situacions sovint són imprevisibles. Com es pot programar d’aquesta manera?
Si treballem en la diversitat , apostant per les respostes personals i veiem que cada nen i nena està en un punt diferent, com podem fer que tots avancin?

Aquests problemes en realitat no ho són. A mida que ens anem fent més experts en aquesta manera de treballar anem constatant una sèrie de fets:

a.-
Els continguts importants, si obrim l’aula a la vida i a la societat, surten sempre i surten des d’òptiques molt diverses. Si el context té per nosaltres tanta importància no podrem avançar tan ràpidament com si ens limitéssim a anar seguint el que diu el llibre, però els aprenentatges són molt més sòlids, i els alumnes no els oblidaran amb facilitat.
Els mestres, però, sí que és important que ens anem familiaritzant molt més amb els continguts, que millorem els nostres criteris per saber què és l’important, que coneguem aquests continguts amb profunditat, que sapiguem, per exemple, a quines necessitats responen (així podrem tenir més bon ull per aprofitar les situacions que ens presentin).
Al final de cada projecte, de cada mes o trimestre, realitzar amb els alumnes el “buidat de continguts” de tot el que s’ha fet en aquell període resulta molt profitós per als nens i nenes, que van prenent consciència del procés en el que estan immersos.
El problema de si algun contingut no hagués sortit té molt fàcil solució. Esperem una situació adequada o , simplement el treballem des del llibre de text (els alumnes saben que hi ha un programa oficial que cal complir)
El que els mestres diem “mecanismes”, com per exemple la taula de multiplicar, és necessari que els nens els aprenguin com sempre. Un alumne que domina les taules estarà en millors condicions per resoldre una situació de càlcul que un altre que es mostra insegur. Però saber els mecanismes, no és la garantia d’una educació matemàtica de qualitat. Les matemàtiques són molt més que fer operacions sense equivocar-se. Cal doncs donar a l’aprenentatge d’aquests mecanismes la seva importància justa sense que ens ocupin la major part del temps i els esforços.

b.-
No podrem programar les activitats de l’aula a llarg termini. Caldrà programar períodes més curts, setmanalment, per exemple. És interessant fer-ho conjuntament amb els alumnes.
Haurem d’estar preparats per improvisar si volem aprofitar una situació “potent” que s’hagi generat a l’aula i no havíem previst.
Si els fulls no estan preparats (em refereixo a que no hem pogut fer la “proposta” a l’ordinador i ciclostil), ho fan els nens i no passa res. Els pares del centre prefereixen que els treballs estiguin ben explicats pel mestre a l’encapçalament per facilitar-ne la comprensió a casa si el nen o nena no se saben explicar, o resulta massa novedós per a les famílies. Malgrat ho procurem fer sempre, val la pena en ocasions aprofitar el moment i fer servir fulls blancs (si és que cal paper, que no sempre es necessari)
No hem de tenir por de que no sorgeixin situacions interessants. Potser ens pot passar els primers dies però després és just al contrari, són tantes les situacions que necessàriament hem de triar, que no podem seguir tots els camins que se’ns van obrint.

c.-
Si coneixem cada cop millor els continguts, ens serà més fàcil treballar en la diversitat. Veurem el punt del procés on és cada alumne i comprendrem millor com avança.
Si no aprenem a moure’ns en aquesta diversitat, si ens fan por les respostes “intermitges” i demanem sempre la solució correcta, acabada, haurem de pagar un preu molt alt. De seguida molts alumnes es despenjaran i reservaran l’ús del seu cervell per a
les situacions extraescolars, ja que a l’escola ,comprendran, que no van a pensar si no a dir el que el mestre vol sentir.
La experiència ens demostra que si ens sabem moure en la diversitat, com a mestres, com a grup d’aprenentatge, tots els nens avancen i es mostren molt més motivats per aprendre. Tots participen del projecte comú, les tasques especials queden eliminades i els grups paral•lels de recuperació. Els alumnes més avançats no s’avorreixen, ja que poden treballar al màxim de les seves possibilitats, no han d’esperar-se per anar fent tots el mateix.
A mida que ens anem fent més experts en aquest “treballar en la diversitat”, l’ambient a l’aula es va transformant paral•lelament, baixa el nivell d’ansietat i augmenta la participació i el sentiment general de satisfacció.
Ho podeu comprovar!