1. El context

A la classe de Les Bruixes i Els Bruixots hi ha 27 nens i nenes.. La primera decisió col·lectiva que prenem és el nom de la classe. Aquest nom afavoreix la identificació i el sentit de pertinença al grup-classe de cadascú. Per això, el moment de decisió del nom és molt important: els nens saben que cal vetllar perquè el nom sigui del gust de tothom i que tothom s’hi pugui sentir còmode i reconèixer, com a mínim, durant un curs. A més, en funció de l’edat, dels interessos i necessitats del grup, del nom de la classe se’n pot derivar un treball d’aula més o menys extens. En aquest cas, decidim que el nom no coincideixi amb el tema del projecte, ja que li volem donar un caire més de treball creatiu, imaginatiu i de fantasia.
El grup, doncs, està avesat a prendre decisions des de principis de curs, tenint present que aquestes afectaran la col·lectivitat i tots se’n faran responsables i s’hi sentiran compromesos. I això cada any.
A l’aula hi ha 13 nenes i 14 nens, dels quals 3 tenen una Adaptació Curricular Individualitzada. Val la pena remarcar que l’atenció a la diversitat de tot l’alumnat es veu afavorida per la manera d’organitzar i gestionar el currículum que tenim a l’escola. Propostes interessants, significatives, complexes, funcionals faciliten que tots i cadascun dels alumnes s’hi puguin apropar a partir de les seves característiques; que el pensament, la mirada i la veu de tots sigui imprescindible per tirar endavant els reptes o per superar les dificultats que el grup-classe presenta en cada moment.
Les Bruixes i Els Bruixots, doncs, conformen una comunitat d’aprenentatge a l’aula que necessita discutir, opinar, escoltar, empatitzar, argumentar, esforçar-se, desanimar-se i tirar endavant, comprometre’s. I això passa cada any i durant tot el curs: des de la gestió pròpia de l’aula (com distribuïm el mobiliari, quins càrrecs fem, com adaptem l’horari setmanal a les necessitats del grup, com buidem els continguts previstos per aquell curs escolar i com els anem desenvolupant, etc.) fins al treball de Tallers, Racons i Projectes, passant pels moments de Treball d’Aula que vagin sorgint.
Les dinàmiques i les relacions que s’estableixen a l’aula vénen condicionades per les característiques dels nens i nenes però també per com treballem. Per tirar endavant un projecte, per exemple, cal compartir moltes idees, neguits, interessos, estratègies, habilitats; ens cal posar-nos d’acord i, per tant, discutir, contrarestar punts de vista, entendre què diu l’altre per avançar en les pròpies opinions. I, sobretot, hem de ser conscients que tots som imprescindibles, que totes les nostres aportacions tenen valor; i ens exigim aquesta implicació i consideració, de manera que les discussions a l’aula, que són moltes, ens suposin un pas més en el nostre procés d’aprenentatge.

2. El projecte

El moment de tria del projecte de curs, per tant, és molt important. La classe de Les Bruixes i els Bruixots explicita les característiques que ha de tenir el projecte: que sigui un tema interessant que no hagin fet mai, que sigui difícil però no impossible, que hi puguem aprendre continguts de diverses àrees, que puguem fer sortides per recollir informació, que puguem demanar a algú que ens vingui a fer una xerrada com a expert.
Escollim Antoni Gaudí com a projecte de treball. Després de veure què en sabem i què voldríem saber sobre Gaudí, proposem vertebrar el nostre treball a partir de tres eixos: la vida, l’època i l’obra. Ens fem preguntes com per què va construir els edificis que va fer (ho va decidir ell? Li va demanar algú? Per què eren tan “diferents”? Només ell construïa així?). Volem saber en quina època va viure (d’entrada ens sembla molt llunyana); i ens preguntem si nosaltres tenim familiars coetanis a ell. Surt el dubte: Gaudí ja era famós, quan vivia? Era ric? Tothom el reconeixia pel carrer? Ens demanem com va aprendre a fer d’arquitecte, si li agradava, en quins moments del procés de construcció d’un edifici intervenia ell; són molt diferents, els arquitectes actuals? Treballen igual? En definitiva, es tracta d’entendre una realitat llunyana per acabar-nos entenent millor a nosaltres mateixos. Reflexionar sobre el passat i el present; les causes i les conseqüències dels processos històrics, socials, culturals, econòmics; analitzar ambdós moments i comparar-ne els trets diferencials.
Una dificultat important a l’hora de decidir com organitzem la feina és que intuïm que la nostra recerca no té un fil conductor estrictament cronològic. Per això, durant tot aquest procés, el dossier personal de cada nen es va ampliant amb materials propis o col·lectius i amb textos individuals o de grup que resumeixen o recullen informacions diverses. Per exemple, una nena va assistir amb la seva mare a una conferència que es feia sobre Antoni Gaudí en una entitat associativa del poble, en va prendre apunts i després ens ho va explicar. O el cas d’una altra nena que ens va portar el full informatiu d’una jornada amb actes sobre el modernisme que s’havia organitzat a Sitges. Donada la possible dispersió que pot suposar la diversitat de temes tractats simultàniament, de tant en tant ens aturem i refem el procés seguit fins al moment; de vegades tots junts i de forma oral, de vegades per escrit, individualment.
Les primeres consultes del material que anem aportant a l’aula (llibres, enciclopèdies, CDs, pàgines web, etc.) ens serveixen per iniciar la biografia del personatge i per decidir quines visites volem fer al llarg del curs: la colònia Güell, la Pedrera, la casa Batlló, el Parc Güell, la Sagrada Família i alguns espais modernista de la nostra comarca. En aquest moment dediquem algunes sessions a calcular el pressupost de cada sortida (autocar, entrada a la Sagrada Família, etc) per preveure quines visites podrem realitzar sense sortir-nos del pressupost.
I decidim fer diversos agrupaments i deixar-nos un cert temps per fer recerca d’informació, cadascú sobre un o més temes d’interès pel projecte. Així, durant unes quantes setmanes, els nens i nenes llegeixen, consulten a internet, veuen vídeos, recullen informacions, dades o comentaris que els han sortit a casa amb les seves famílies, etc. A la vegada, continuem la recerca d’informació i comencem a preparar la visita a la Colònia Güell. Abans d’anar-hi, tots mirem un CD sobre la colònia que ens acosta per primera vegada a la vida dels treballadors de les colònies tèxtils de l’època. Veiem fotografies reals on apareixen nens i nenes vestits de manera diferent a la nostra. Comentem, per exemple, informacions sobre com era l’escolarització, com eren els pobles (aquí decidim que algú s’ha d’encarregar de buscar informació sobre Sant Pere de Ribes i Barcelona), la indumentària (surt el tema del negre com a senyal de dol).
La visita a Santa Coloma de Cervelló és una font riquíssima de vivències i informacions. L’equip de guies adapta les seves explicacions a les nostres necessitats; fem fotografies de tots els racons; passegem per tot el poble i fins i tot ens deixen visitar una fàbrica que actualment està en funcionament i que conserva l’estructura original; ens prenem un moment per poder dibuixar i fer esquemes de diferents detalls de la cripta, per dins i per fora. Una primera conclusió confirma el que ja pensàvem: La colònia, l’església inacabada amb la cripta, la història de la família Güell i la seva relació amb Gaudí, etc. reflecteixen un entramat de relacions que estan en l’origen i configuren el desenvolupament de la seva obra, vida i el moment en què va viure.
Arriba Nadal i agafem el compromís d’aprofitar les vacances per parlar amb familiars. Farem un arbre genealògic que reflecteixi el nom i cognoms, la data de naixement i mort, si s’escau, i l’origen de germans, pares, oncles, avis, besavis, rebesavis... fins on puguem arribar.
En tornar de les vacances, preparem una petita exposició dels arbres genealògics (passar a net, situar en mapes els indrets d’on provenen els nostres familiars, etc.).

I, paral·lelament, reprenem les vivències de la visita a la Colònia Güell.

3. La història dels rals

Un grup llegeix en un llibre sobre les colònies tèxtils que els treballadors cobraven 20 rals per setmana treballada, i que treballaven de dilluns a dissabte. Ho comenten i veiem que no sabem què són els rals. Per això un altre grup queda encarregat d’investigar-ho. A partir d’aquí dediquem un temps ampli a treballar la vida a les colònies tèxtils. Aquest coneixement es complementa amb altres aportacions d’alguns familiars (avis i àvies) sobre com vivien ells quan eren petits.

5. Altres connexions

Paral·lelament, anem preparant les properes vistes a la Pedrera, la casa Batlló, el Parc Güell i la Sagrada Família. Per la visita al Parc Güell ens cal fer un treball previ sobre plànols, ja que allà a cada grup s’orientarà a partir del que hem aconseguit per internet. Abans d’anar-hi (ningú hi havia estat abans) ens l’imaginem a partir de les dades que ens dóna el plànol i de les imatges i el que llegim en diferents webs. De vegades el treball és més intens en la preparació, de vegades en la devolució de la visita. En el cas de la casa Batlló, cadascú va imaginar, descriure en un text, dibuixar i realitzar amb caixes de cartró i altres materials una casa “a l’estil” de la casa Batlló.

Aquí tenim el complement sobre la informació de l’època: la burgesia catalana de la Barcelona de l’època. Coneixem com vivien, la indumentària, els habitatges, les professions (les dones no treballaven i els nens tampoc), els vehicles que usaven. Van creixent els elements que ens serveixen per comparar i completar la visió de la societat de l’època. A més, descobrim que s’escrivia en català, però de manera diferent a la nostra. Per això un grup s’encarrega de buscar informació i materials (llibres de principis de segle) sobre com s’escrivia en català abans i després de la reforma fabriana, qui era Pompeu Fabra, etc.

De tant en tant anem explicitant el procés: recordem l’índex, què volíem saber, què hem fet fins ara, què ja no ens interessa tant o què considerem prioritari. Desestimem algunes idees: per exemple, seguint els criteris que presideixen l’estètica modernista i gaudiniana, com dissenyaríem nosaltres ara una paperera, un cotxe, un fanal, la biblioteca municipal...
Arriba un moment en què ens interessa aprofundir sobre la professió de Gaudí. De les diferents visites i altres fonts d’informació, ens hem anat fent una imatge del Gaudí arquitecte. Des dels seus orígens humils fins a la seva prolífica obra, donada la magnitud de cada construcció. Per això ens posem en contacte per correu electrònic amb en Miquel Mas, un arquitecte de Vilanova i la Geltrú que s’avé a passar un matí amb nosaltres i compartir la seva feina.

Preparem la visita i decidim explicar-li el projecte que estem realitzant. Acordem, però, que aprofitarem la seva estada per aprendre, sobretot, tant com puguem sobre la professió i ens allunyarem de Gaudí. En Miquel ens mostra estris antics per dissenyar, ens parla dels que nosaltres tenim al nostre abast i ens ensenya el seu ordinador portàtil amb els programes en 3D que li serveixen per visualitzar les obres acabades.
Aquesta visita ens provoca l’interès per dissenyar i construir maquetes nosaltres mateixos, seguint algunes de les seves indicacions. Afegim, doncs, un altre camp obert de treball: construirem un poble. Comencem posant-nos d’acord sobre els edificis que hi haurà, seguint el que tenim a Sant Pere de Ribes en l’actualitat. Al llarg del curs, al racó d’arquitectura alguns nens han practicat fent rectes paral·leles i perpendiculars. Altres han iniciat un treball d’escala i de proporcionalitat. Necessitem que ho comparteixin amb tot el grup per tal d’unificar criteris i tenir recursos per la construcció. Individualment o per parelles, dissenyen i construeixen la seva part del poble de tots.

6. Acabem el projecte

S’acosta el final de curs i veiem que el treball al voltant d’informacions i experiències s’ha anat teixint considerablement. Ens costa decidir com organitzem tota aquesta informació. Per això decidim que el dossier de cadascú recollirà els escrits, fotos, dibuixos, textos de càlcul, mapes, resums, reflexions, etc. De manera cronològica. Però que per compartir amb els altres (companys d’altres cursos, família, amics) ens interessa alguna altra fórmula que no sigui tan lineal. D’una extensa conversa molt controvertida sorgeix la idea de plasmar els que hem après en forma de web. Pensem que el llenguatge d’internet facilita reflectir les connexions i passejar lliurement seguint el criteri i l’interès de cadascú. Demanem al Manel Garcés, informàtic, pare de l’escola, que ens orienti sobre el tema. Amb ell aprenem a escanejar fotos i textos, a reduir i ampliar documents, a importar d’internet, crear hipervincles, etc.

Decidim que no tenim temps per passar a l’ordinador tot el que hem treballat, així que a partir d’un índex seleccionem les informacions o les experiències que més ens interessa compartir amb els altres. Els procés d’elaboració de la web, que penjarem a la de l’escola, és llarg i costós. Finalment, però, ens en sortim i acabem el curs satisfets.

Presentació

Ja s’ha comentat el marc en el que s’origina el treball que presentem a continuació. Podríem haver escollit un altre aspecte matemàtic del projecte per mostrar-lo de manera detallada. En la decisió presa hi prenen part tant qüestions de documentació (és un treball del que disposem de molta documentació, especialment en forma de transcipció de converses), com especialment el caràcter de les relacions entre els elements socials del treball i els elements matemàtics presents en aquest context que hem denominat “Història dels rals”.

Podem dir que és una història matemàtica carregada de significats socials, o bé una història sobre la vida de les persones d’un moment històric determinat de la nostra societat, que requereix de l’ús de les matemàtiques per entendre-la.

Aquest lligam entre persones i matemàtiques, persones vinculades a un moment social i històric molt concret, persones que viuen d’una manera determinada, que tenen unes necessitats determinades i que organitzen la seva vida de treball, de quotidianitat d’una manera concreta, s’expressa a partir del valor del seu treball i del valor de les coses que necessiten per viure, del valor econòmic i també del valor emocional, que és el que ha vinculat més en especial els nostres alumnes amb les persones de l’època de’n Gaudí.
Si bé doncs, des del punt de vista matemàtic, la podem veure com a una història de proporcionalitat, és principalment una història de vinculació històrica amb la comunitat cultural de la que els nens i nenes de la classe formen part. Les matemàtiques esdevindran en aquest context, principalment una eina privilegiada per facilitar aquests vincles i aquestes relacions entre el ser i el pertànyer de les persones que configuren la comunitat de l’aula...

Respecte de l’organització del treball:

Hem volgut mantenir un relat basat en el fil temporal del que va passar al llarg de les 7 sessions que configuren el nucli fort d’aquest treball.
Com que la situació i els elements cognitius i emocionals que es movilitzaven en les diferents sessions eren molts i sovint complexos, hem optat per presentar cada sessió des d’un eix explicatiu i interpretatiu diferent, de manera que focalitzem la valoració de la sessió a partir d’algun element que forma part de la manera comuna en què ens plantegem a l’escola el treball també amb les matemàtiques. Elements bàsics com la diversitat i la interacció, l’organització de la informació, la conversa i l’argumentació, la complexitat, l’ús de llenguatges simbòlics o els vincles entre situacions, etc.

No obstant, aquesta opció no pot amagar que en diferents capítols hi podem rastrejar elements de gairebé tots els altres. Focalitzar un punt de vista ens ha permés una presentació més intencional i diferenciada de la que en realitat sovint es donava en el dia a dia a l’aula.

Informació, interacció i diversitat

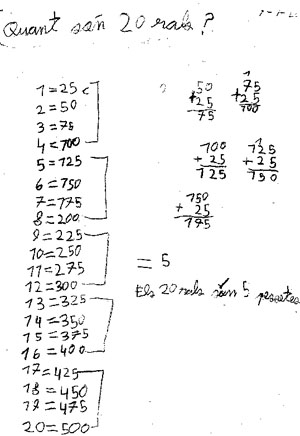
¿Quantes pessetes són 20 rals? (09-01.03)

Presentació de la situació

En el desenvolupament del projecte de Gaudí, uns nens han trobat la següent informació:

Aquesta informació es comenta a la classe i un grupet de tres nens i nenes queda encarregat de buscar més informació sobre el que són els rals. Als pocs dies ofereixen aquesta explicació a la resta de la classe:

La mestra proposa trobar QUANT SÓN 20 RALS EN PESSETES?.
Com que els tres nens que hi havien treballat ja havien buscat aquesta informació, van oferint el seu ajut a la resta de la classe mentre cada nen va elaborant les seves idees.

El VALOR DE LA INFORMACIÓ.

Una primera qüestió que ens interessa remarcar, abans de l’anàlisi de les produccions dels nens, és la manera com s’ha gestionat l’arribada de nova informació al grup:

- Ens porta també a pensar en el valor que té que uns aportin informació i després sàpiguen transformar-la, fent-ne partíceps a tota la classe.

QUINA HA ESTAT LA MANERA COM ELS NENS S’HAN ENFRONTAT A LA TASCA?

Tot i la dificultat intrínseca de la feina proposada, que implicava la necessitat d’establir relacions sistemàtiques d’equivalència entre tres tipus diferents de quantitats, la manera d’actuar dels nens és molt lliure i oberta i es basa en els dos elements següents:

- Primer escullen una de les dues informacions de la definició com a element organitzador del seu text de càlcul. La majoria sobre la relació entre rals i cèntims. Aquesta opció sobre la informació serveix com a base matemàtica que s’utilitzarà per a la producció del treball posterior.
- A continuació elaboren aquests textos de càlcul, guiant-se per un costat per l’opció d’informació que han pres, i per un altre per la seva capacitat i domini d’utilitzar els nombres i la seva composició i, finalment, pel sentit lògic (d’addició repetida, d’agrupament múltiple, de part-tot, de proporcionalitat, etc.) que poden assignar a l’operació implicada en la seva opció.

QUINES SÓN LES IDEES QUE REFLECTEIXEN ELS SEUS TREBALLS?

Veiem ara alguns dels treballs més significatius de manera que ens permetin valorar la riquesa de pensament i la capacitat de treball de l’alumnat quan té la possibilitat de treballar de manera creativa i lliure.

Hem categoritzat els diferents treballs en quatre classes, intentant imaginar el pensament del nen quan pren opcions d’escriptor de càlculs, independentment que hagin pogut resoldre o no la situació.

1. Fer 20 vegades 25.Utilització d’una unitat simple

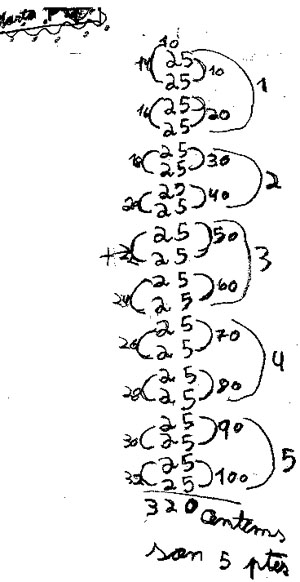
Text de la M

La M. ha buscat al seu repertori de mecanismes de càlcul algun que ella pugui utilitzar i que li pugui servir per justificar una resposta conseqüent: ha d’arribar a 5, que és la quantitat de pessetes que sap que valen els rals.

Com ho fa?

Si bé hi ha 20 vegades 25 (deu ser el que fa primer, escriure el llistat) després ho intenta sumar. En aquest procés, es perd en el resultat, ja que a partir del 16 ha anat comptant com confonent la quantitat de valors de cada parella (2) amb la suma total de les desenes. Per això no li dóna 50 desenes(500 cèntims), encara que no es perd tant en el significat. Avalua el seu resultat aplicant un altre criteri de càlcul diferent: que 4 de 25 fan 1, 4 més en fan 2, etc., que és el que anota a la dreta del text de càlcul.

És a dir, ha actuat intentant ser conseqüent amb la informació que té disponible: per un costat els seus coneixements de càlcul li permeten imaginar que el resultat ha de venir de sumar 25 cèntims 20 vegades. D’una altra, en veure que no li surt el resultat previst, utilitza l’altre criteri. No té tant una intenció de validar el seu primer text de càlcul, ja que no utilitza cap marca per reflectir la contradicció amb l’altre resultat, sinó que busca un mecanisme de validació del resultat que ella espera.

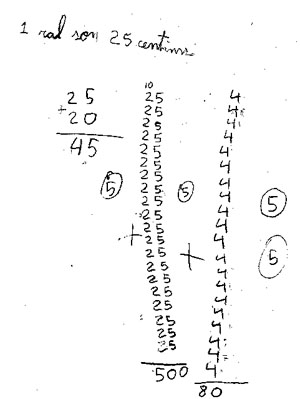
Text de la C

El text d’en C. també reflecteix aquest doble pensament: sobre la quantitat total d’unitats de 25 a sumar per una banda, i sobre el valor de partició que la unitat 4 efectua sobre la quantitat total de cèntims per una altra. En C. primer suma 20 i 25, cosa que ja dóna idea de les seves confusions entre el sentit de cada quantitat. Després suma 20 vegades el 25. Ho fa correctament, ja que li dóna 500, però perd el significat del que està fent: no sap què són, ni què tenen a veure amb la resposta esperada, és a dir com es relaciona amb el nombre de pessetes (5). Possiblement ha perdut de vista que els 500 són cèntims, i que cada 100 cèntims val per una pesseta, és a dir, no pot considerar el conjunt de la informació que té disponible. Com que el 5 és un element referencial el va posant en el seu text, però sense cap relació amb els càlculs que fa. En aquest moment es veu clarament que en combinar les dues informacions s’ha perdut. Per això, torna a fer el mateix amb el 4, sumant-lo 20 vegades, confonent les relacions numèriques entre el nombre de parts (4) i el valor de cada part (1/4), de manera que el nombre ¼ no té un significat diferent de 4. Confon el nombre de parts del tot amb el nombre de vegades que ha de repetir aquesta part.

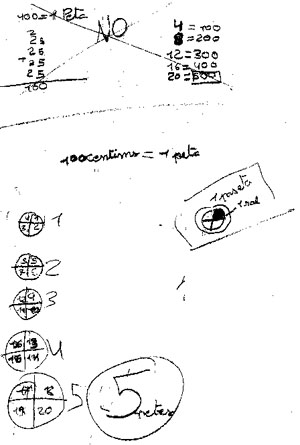
2. Cada 4 de 25 fan 1, sense incorporar la idea de ¼ (de relacions part-tot) sinó que potser es centren en la informació que 4 de 25 fan 100. Es basa en com construir una unitat d’ordre superior

Text de la I

L’I. estableix una clara correspondència entre els rals i els cèntims, i després entre aquests i les pessetes, agrupant les quantitats anteriors de 4 en 4. Tot i així, no manifesta clarament com sap que 100 cèntims són 1 pesseta. En realitat no usa unitats compostes...
Per a realitzar els càlculs es recolza en les sumes de la dreta. Necessita fer les sumes fins que s’adona de les regularitats: en la darrera suma, que és semblant a la primera, abandona la repetició del recurs i actua directament sobre la taula de correspondència de les tres quantitats.
L’A. estableix equivalències ben definides entre els cèntims i les pessetes (100 = 1 PTA), però no queda tan clara la relació entre els rals i les pessetes: ho fa sempre a partir de les relacions entre rals i cèntims.

Ella sí que usa les diferents unitats de comptatge i les relaciona clarament entre sí, sempre, però, a partir de les pessetes.

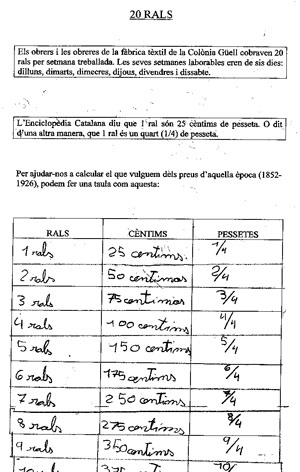
3. Treballar amb la informació ”un quart” ¼, buscant mecanismes (gràfics) per construir el càlcul

Text de la P

La P. estableix interessants relacions entre els cèntims i les pessetes, però sobretot entre “cada 4” i els cèntims (i les pessetes??). Però el que fa al principi no li sembla prou clar, com a mecanisme argumentatiu, com si fos per a ella una espècie de cosa intuïtiva que no sap explicar prou bé.
Aleshores, ho torna a fer amb dibuixos, establint relacions de part a tot i explicant en el requadre el seu argument: el mecanisme calculador és el ¼, i amb els dibuixos va controlant i argumentant sobre el càlcul, com si estés elaborant una especie de taula: 4-1, 8-2, fins arribar a 20, que són 5. Possiblement la via del 1/4 li sembla més clara com a manera d’explicar d’on surten les 5 pesetes.

4. Pensar globalment en les relacions entre les 3 quantitats, imaginant com creixen respectivament, és a dir, com s’afecten mútuament.

Primer escriu les dues definicions, com si el fet de repetir-les, expressant les 3 unitats, hagués de tenir conseqüències per als mecanismes de càlcul. És a dir, valorar la informació disponible i fer-la conscient des del principi és molt important per a aquest nen. Transforma aquesta informació, amb un dibuix que li serviria també com a base de càlcul però, de fet, el sistema més fàcil usant nombres és per a ell el que fa servir com a base en la segona definició. Per això, a continuació es fa com una pregunta hipotètica:”1 pesseta quants cèntims té?”, i ho fa com pensant en el que cal saber per utilitzar adequadament la segona definició del text. La resposta és com un parlar amb si mateix, per a buscar una manera apropiada d’argumentar. No obstant, després són les relacions entre les dues definicions les que fa servir per als mecanismes de càlcul escollits: elabora com una taula entre pessetes, rals i cèntims com a mecanisme per calcular.

L’E. relaciona globalment les tres quantitats al mateix moment. A partir del 100 utilitza aquesta quantitat com a unitat composta, sense necessitat de repetir els passos anteriors (125, 150...) i és capaç de fer-ho fins a arribar a tenir clara la informació de la darrera línia: l’equivalència 5 ptes=500 c=20 r.
És interessant remarcar com el signe = s’utilitza molt poc com senyal d’equivalència en el conjunt d’aquestes produccions, ja que per als nens té principalment un significat de resultat.

EL PERQUÈ DEL QUE FAN ELS NENS I DE LA SEVA MANERA D’ACTUAR

- La primera qüestió que ens interessa remarcar és la manera com actuen els nens. La seva tasca és la d‘escriptors de textos de càlcul que utilitzen per organitzar i avançar en el seu pensament. Organitzen les seves produccions amb una finalitat clara: saben el que volen trobar, per a què ho volen trobar, i fins i tot, en alguns casos més que altres, coneixen el resultat. Però han d’escriure una argumentació clara per al seu pensament, una argumentació que és una elaboració mental que els ha de servir com a mecanisme d’aprenentatge en qüestions tan importants i complexes com la multiplicació (relacionada amb la proporcionalitat), la correspondència múltiple, la composició de quantitats, l’equivalència, la idea de valor... Per a fer això es plantegen un problema, han de valorar una situació i han de dotar d’un sentit a aquests números, per tal d’establir les relacions entre ells per poder resoldre’l. És a dir, la manera com organitzen els seus textos reflecteix les estratègies que utilitzen per calcular i la capacitat que tenen per fer conjectures, imaginar possibilitats, valorar els seus resultats, etc. Per això podem dir que els seus textos tenen un alt valor argumentatiu.

- La segona qüestió es refereix al valor de la informació . El principal sentit d’aquesta informació és que remet el problema de treball a un projecte més ampli, que és el que li dóna sentit i continuïtat.
Aquesta informació permet la contextualització i la construcció d’un sentit per a la situació, a partir del fet d’escollir elements de la seva comprensió tant del context com del sentit lògic dels nombres i les operacions. Aquesta contextualització conté elements de diferents nivells: el que aporta la dinàmica del mateix grup; el projecte, uns nens que aporten informació, ajuden…; però també la rellevància del problema que està present lligat a la manera de viure de les persones i el fet que posa les persones en el centre de l’activitat de calcular, relacionada amb un context històric llunyà però encara proper, o la relació amb el significat cultural dels sistemes de monedes i de compra-venda…

- A més, la manera com aquesta informació s’ha gestionat, la manera com s’ha treballat, implicant l’alumnat de la classe per generar-la, per fer-la circular, per generar noves preguntes, per valorar els resultats diversos, ha estat definitiva en la manera com tots i cada un dels nens han entès el seu protagonisme de treball. Disposar d’una informació prèvia clara i oberta, que aporta possibilitats diverses de treball, que serveixi com a base d’elaboració del problema ha estat importantíssim. Hem vist de quina diferent manera els nens decideixen escollir una part o el conjunt de la informació, però a més, hem de valorar les possibilitats d’interacció que ha creat. Tot i que el treball d’elaboració textual ha estat personal, les relacions entre els nens no es deixen de banda. Especialment el grupet que va aportar la informació va tenir un paper bàsic en la regulació de la informació i en la gestió de la dinàmica de treball...
Compartir informació permet l’argumentació i la capacitat explicativa que aporta la situació, en aquest cas, tant respecte de la comprensió del salari dels obrers de la fàbrica (per exemple, permet plantejar-se posteriorment la pregunta: i això és molt o poc? És suficient?) com respecte de la comprensió dels processos de càlcul que utilitzen els companys i la relació amb el sistema de monedes, també les actuals (cèntims). Aquesta capacitat explicativa s’ha de vehicular didàcticament, per exemple a partir dels mecanismes de devolució que funcionen habitualment en el grup, com veurem més endavant.

- Finalment, cal manifestar la diversitat i riquesa col•lectiva dels textos de càlcul: és importantíssim respectar aquesta diversitat com a valor de la identitat personal de cada nen (com poden escollir una o altra de les informacions, com elabora cada un les relacions que per a ell son més significatives...) però també com a condició bàsica per a la creativitat en els mecanismes de càlcul. No podem pretendre que els nens desenvolupin capacitats com la de conjecturar i hipotetitzar, la d’ ajustar i reflectir processos, la d’argumentar i analitzar el propi pensament, etc., si no tenen llibertat per enfrontar-se amb els problemes de manera lliure, creativa i personal, de manera que puguin organitzar les relacions que ells poden establir entre els nombres, decidir quins recursos representatius i simbòlics entenen i són capaços d’utilitzar, valorar quina és la trama explicativa que té el text que estan elaborant…
Però la diversitat té sentit també en el valor i la riquesa que pot aportar a l’argumentació i la construcció del sentit col•lectiu de significats a l’aula.
Per això, el valor de la diversitat no consisteix només en el respecte a les possibilitats de cadascú, en l’afavoriment de la seva integració a l’aula, sinó que aquest respecte està definitivament vinculat a l’afavoriment de la riquesa de l’aula, que passa per l’ampliació dels recursos personals de tots i cadascun dels nens i nenes de l’aula.

ALTRES QÜESTIONS QUE ELS MESTRES ENS PODEM PLANTEJAR A PARTIR D’AQUESTA SITUACIÓ

1. Com ajudar a estructurar aquestes idees, de manera que el coneixement que circula a la classe sigui vist com a un coneixement disponible en altres moments i situacions
2. Com es programa la continuació per tal que sigui VIVA, cosa que implica tres condicions al menys:
- Mantenir el vincle amb la situació, és a dir, no perdre’ns en els aspectes lògics i de càlcul
- Mantenir el context: intern de l’aula i extern (per exemple les aportacions dels avis, o la documentació històrica sobre la vida en aquella època…)
- Generar comunicació i conversa com a fonamental per continuar generant elements de coneixement personal


COM es programa la continuació per tal que sigui VIVA: - Mantenir el vincle amb la situació
- Mantenir el context
- Generar comunicació-conversa


Apèndix: POSSIBLES CONTINGUTS IMPLICATS EN EL TREBALL

- La Multiplicació (relacionada amb la proporcionalitat).
- Correspondència múltiple
- Composició de quantitats
- Equivalències, sense el signe =

- Idea de valor
- Sistema de monedes: valor de les diferents unitats, equivalències entre elles
- Canvis històrics…

- Plantejar-se el problema
- Imaginar un sentit per als números que permeti resoldre un problema
- Relacionar problemes i operacions

- Organitzar textos i estructures per calcular
- Calcular de diferents maneres
- Estimar els resultats com a vàlids i/o possibles

- Generar estratègies
- Ajustar i reflectir processos
- Fer conjectures, hipòtesis, investigar…
- Organitzar, plasmar, transmetre idees

- Analitzar el pensament dels altres
- Organitzar el pensament de forma clara i coherent

- Interpretar fenòmens socials
- Establir connexions
- Construir valors socials
- Construir valor sobre la pròpia matemàtica

La consideració de l’aula com a un espai d’interacció de veus diverses, que construeixen coneixement en comunitat, implica la necesitat de considerar que un dels objectius principals del treball del mestre és imaginar com pot contribuir a la construcció de l’aula com a un projecte de comunicació.

REGISTRE DE LA SESSIÓ

La conversa consta com a mínim de tres parts ben diferenciades. El punt de partida de les tres és comú:
Els nens i nenes estan fent el projecte sobre Gaudí. Fa dies que varen visitar la Colònia Güell i varen buscar informació sobre la vida dels treballadors de la fàbrica. Varen saber que en aquella època el sou era de 20 rals per treballar sis dies a la setmana i ara estaven dins del procés de saber què volia dir 20 rals i si això era molt o poc. Han elaborat els sesu textos de càlcul i ara és el moment de parlar-ne.
No obstant, veurem com qualsevol conversa s’obre a noves possibilitats en funció de les intervencions d’uns i altres i de les intencions que ens mouen a l’actuar. Crear una intencionalitat col.lectiva per a l’aula com a projecte de comunicació, és una de les funcions de la conversa.

1. Els treballadors de la Colonia Güell guanyaven 20 rals per treballar sis dies a la setmana

Tutora.- Anem a explicar a l’Albert i la Bea (mestres suport) el treball que vàrem fer l’altre dia per saber quant eren 20 rals.

Entre tots.- Uns nens van trobar a l’Enciclopèdia que un ral valia una quarta part d’una pesseta, 25 cèntims. 20 rals són 5 pessetes. (cada grup ho havia calculat a la seva manera el dia anterior)

Tutora.-Què us sembla?
N.-També treballaven el dissabte, el diumenge feien festa.
A.-(Aixeca la mà)
P.- Els nens feien sis dies d’escola.
A.- Imagina’t que avuí és festa,doncs ells tindrien un dia més de treball
T.- Exacte: Tenien un dia més de treball i guanyaven 20 rals.
X.- Era poc, eren 5 pessetes

T.- Com ho vam fer per saber que eren 5 pessetes?
E.- 1,2,3,4... fèiem un grup. 5,6,7,8... un altre grup... fins arribar al 20. I tots els grups feien 5 pessetes.
T.-Per què fèiem grups de 4?
P.- Perquè 25 cèntims és un ral. Una pesseta té 100 cèntims, n’hi ha 4.
D.-25,25,25 i 25 fan 100.
T.- Què podem fer si volem recordar què més vàrem dir
Grup.-Mirem el full

(Treuen el full que van fer el dia anterior de la carpeta: Són els fulls que s’han analitzat en les pàgines anteriors) L’A. no el troba. La C. que és al seu costat li ajuda a buscar-lo. El full no hi és.

T.-Com sabíeu que un ral eren 25 cèntims.
N.-Van trobar a l’Enciclopèdia que un ral era ¼ de pesseta.
T.- I això què té a veure amb 25 cèntims?
L..- (Dibuixa a la pissarra una rodona i la parteix en quatre parts) És un pastís i faig quatre parts i a cada quart hi ha 25 cèntims.
T.-Com ho saps?
P.- Si a una pesseta hi ha 100 cèntims, jo vaig sumar 25 quatre vegades i així havia comprovat que 25+25+25+25=100
Albert.- Vejam si ho he entés bé: A l’enciclopèdia vàreu trobar que un ral era ¼ de pesseta, (al dibuix del Luca escriu a una part: ¼, 1ral=25 cèntims)
Quants rals són la pesseta?
S..-4, perquè necessitem quatre quarts
Albert.-Això no és un pastís. Representa una pesseta. No la podem partir de veritat, els senyors de l’época d’en Gaudí no la voldrien!; l’hem de partir en el nostre cap.
La meitat quants quarts serien? Quants rals serien mitja pesseta?
L..- 2 rals són mitja pesseta
Albert.- (Escriu a la pissarra: 2 rals= =1/2 pesseta)
Què hi pots posar aquí al mig?
R.-50
Albert.-50 pessetes?
R..-Sí
Albert.-Qui li ajuda
D..-Cèntims
Albert.- Qui no hi està d’acord?
D.- Jo crec que 25
Albert.- 50 o 25?
P.- 50 , perquè 25 i 25 fa 50 i n’hi ha dos
D..-Sí
Albert.-I quantes pessetes?... Mitja! Esteu fent una cosa molt important, esteu pensant en pessetes, cèntims,rals. N.- I per què no ho fem en euros?
N.-Perquè és l’época d’en Gaudí
Albert.-(Assenyala la “pesseta” de la pissarra partida en quatre parts) Aquí caben 20 rals?
Grup.- No
Albert.-Quantes en necessitem per fer 20 rals?
J.- 5, perquè ja ho havia fet (fa referència al full del dia anterior)
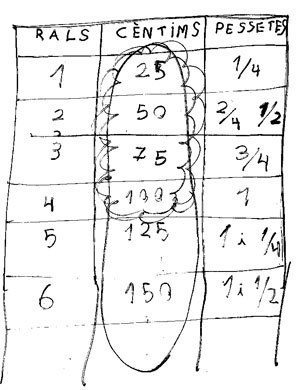
Albert.-Els nens grans per ajudar-se a pensar fan una cosa com aquesta

Em sembla que els nens grans ho farien així, no perquè vosaltres no ho feu bé sinó perquè ells pensarien que seria més fàcil comptar fins a 20 o més rals.

2. La conversa ens permet obrir nous camins

Com que l’objectiu de la conversa no era tancar sinó obrir, les intervencions dels nens poden ser recollides encara que no siguin ajustades al moment en què es diuen:

Albert.- Abans un nen (en Xavi) ha dit que era poc, 20 rals
E. .- La mare m’ha dit que un dinar a l’avi li costava 1 pesseta i mitja
T.- Com ho pagaríem?
Albert- Seria de l’època del Gaudí?
Grup.- No
J.- Coges una peseta y la partes (s’aixeca de la cadira i fa el gest amb cara de broma)
Albert.- Si un dia val una pesseta i mitja, dos dies tres... amb cinc pessetes passarien molta gana.
P..- Ara una pesseta no és molt però abans es valorava molt
T i Albert.- Com ho podem saber si 5 pessetes eren molt o poc?
N.- Als llibres
X.- A l’ordinador
L.- Poses la paraula rals i et surt la informació

T.- Imagineu-vos que som una família els nens d’aquesta taula i jo sóc la mare i la única que treballo i guanyo 20 rals a la setmana. En què me’ls he de gastar?

G.-Menjar
X.- (Aixeca la mà)
R.- Electricitat
X.-Amb les necessitats com...roba
J.-(Aixeca la mà)...no me’n recordo
C.- Impostos
L.- Aigua
M.- Metges
A.- En comprar un cavall
P.- No és una necessitat, anaven caminant
A.-No podien si era lluny
L.-Xampú per si tenien polls
A. i An.-( estan molt atents. L’Adn aixeca la mà)
X.- Es banyaven al riu perquè no hi havia dutxes
P.- El riu no s’havia de pagar
An.- Un pont perquè passi la gent
T.-Estem parlant d’una família, no de les necessitats de tot un poble
C.- Jo crec que el més important seria menjar, aigua i roba
O.- Comprar
S.- Algunes mantes per si fa fred
T.- Ho posarem dins de la roba
R.- Per l’escola
T.- Els nens pagaven l’escola?
X.- Els que treballaven a la fàbrica, els fills no havien de pagar escola
T.-I què més els donaven?
Grup.- La casa
L’An i A estan molt interessats, aixequen la mà, somriuen...
P.- La meva mare em va dir que cada dia els diners es valoren més
Albert.- Què vol dir valorar?
C.- Que valia molt
Ll.- Eren pobres. Amb els rals podien comprar poc.
N.-Tots eren molt pobres
N.- Tots no eren pobres, el senyor Güell no ho era, era ric
Albert.- Valorar vol dir que podem comprar més coses?
T.-Si amb 20 rals podien comprar molt menjar, molta roba, un carro i un cavall...volia dir que era molt. Si només podia comprar una mica de menjar, una mica de roba seria poc. No ho sabem
D.-1 pesseta passa a 3 pessetes, 1 euro passa a 20 euros, passa de valor.
Potser que a Anglaterra eren molt rics i a Espanya més pobres

3. Les monedes i la història: vincular-nos a una comunitat que canvia amb el temps

T.- Teniu pessetes d’abans?
J.- El meu pare en col•leccionava
A.- Al meu avi, el Pare Noel li va portar una moneda molt antiga
S.- A casa meva vaig trobar un bitllet de l’època medieval i estava mig trencat.
Albert.- Com ho saps que era d’aquesta època?
S.- M’ho va dir el pare
An.- El meu germà es va trobar un moneder així de gran
C.- El meu avi li va donar al meu pare monedes antigues i les tenim en una caixa
O.- Jo tinc molts dòlars perquè a Santo Domingo no es paga ni amb pessetes ni amb euros. (fa poc que va anar de vacances)
R.- Jo vaig trobar una moneda francesa i antiga
M.- Jo tinc monedes antigues
X.- Jo tinc un pot de monedes barrejades
L.-El meu avi té un pot ple de cèntims, pessetes, monedes antigues, bitllets
T.- Els rals eren monedes o bitllets?
Grup.- Monedes
C.-Jo tinc una moneda molt antiga, de mil nou-cents i “algo”
Albert.- (Ensenya la caixa forta que ha portat). Què penseu que hi ha aquí dintre?
Grup.- Pessetes, rals, cèntims, bitllets de ral, diners antics
N.- D’on ho has tret
Albert.-He excavat un forat buscant un tresor (amb cara de broma)
O.- Potser és dels teus avantpassats que ho han anat passat fins a tu
Albert.- De quina época, de Gaudí? Com ho podem saber?
N.- Amb l’any
Albert.- Sabeu si quan va neixer Gaudí la pesseta ja existia?
Grup.- No
Albert.- I quan va morir?
Grup.- No
Albert.- La secretària ho podria comprovar.
(Obre la caixa i ensenya 10 cèntims, un bitllet de pesseta, una moneda de 50 cèntims...)
Albert.- Quantes pessetes són 50 cèntims?
An.- Dos
Albert.-( Ensenya dues monedes de 50) Quantes pessetes són?
P.- 1 perquè ½ i ½ són 1
Albert.- Aquestes monedes no es poden llegir. Us sembla que són més antigues?
Grup.- Sí
Albert.- Perquè no es llegeix?
E.- Perquè es fa vell com les persones
An.- (S’aixeca per tocar les monedes)
Albert.- Veiem l’any, l’any...1878, 10 cèntims encara més antics 1866...Eren de l’epoca de Gaudí?
(els nens comproven que Gaudí va neixer el 1852). 10 cèntims eren més poquet que un ral.
P.- Jo tinc una pregunta: Els de 1866 saps quan es van acabar?
Albert.- No, es pot buscar
A.- Jo tinc una moneda antiga a casa que és d’Anglaterra
Albert.- Us ho deixo. M’els ha deixat una amiga meva que és molt velleta quan li he dit que estàveu estudiant els rals, així que cuideu-los molt.

• I després d’obrir, ...aprofundir una mica: La riquesa de la conversa ha estat tan gran que quan la mestra se n’adona proposa al grup aprofundir una mica més en la línia encetada Els alumnes han estat molt interessats durant tota la conversa, que ha durat més d’una hora i mitja, però potser la quantitat de temes tractats fa que sigui convenient establir algun mecanisme per tal de recollir allò que per als diferents nens i nenes hagi estat més important. Per això, fa la següent proposta:

T.-Ara sols o en parelles o grup de tres agafeu un full i penseu què necessiteu apuntar per recordar: preguntes que volem saber, informacions de la pissarra que us semblin interessants per guardar.

L’An. no sap amb qui posar-se i no ho vol fer sol. Els altres ja estan treballant. Ell volia treballar amb el J però ja té parella. Els proposem ser tres i accepten. Sento la proposta de l’An:
Apuntem. Són molt o poc 20 cèntims?

Podem comparar rals, pessetes i cèntims?

Aquesta és una problemàtica concreta que no és l’eix inicial del següent treball, sinó que deriva de la informaciío i la discussió de la sessió.
Com es veurà, el problema en un primer moment no és la comparació entre les diferents unitats recollides en les informacions, sinó organitzar i entendre la informació recollida, i fer-ho de manera que ens permeti valorar les necessitats reals de les persones i la relació entre aquestes necessitats i els preus de les coses. Només posteriorment, en la mesura que els preus (i els sous) s’estableixin amb monedes diferents, serà necessari establir mitjans ràpids de conversió entre monedes, que permetin la seva comparació, quan s’adonen que els preus de les coses els han trobat amb monedes diferents.

- Es comença la sessió fent referència als treballs realitzats pels diferents grups, i preguntant si havien trobat informacions sobre preus de l’època d’en Gaudí.
Al marge dels diferent documents consultats, les famílies (sobretot els avis) han estat una important font d’informació. Els nens i nenes van aportant dades que fan referència als preus, a intercanvis en espècies i a fets de la vida dels seus avis (Guerra Civil).
Durant la setmana, els alumnes han realitzat una sessió de treball per grups, cada grup tenia uns objectius de recerca d’acord amb la documentació que havien recollit que feia referència als interrogants oberts la sessió del dia 15. Aquests són alguns dels treballs dels grups

A.- Quan la meva àvia era jove canviava patates per or.
Albert (mestre suport).- Quina mena d’or, monedes d’or, or a pes...?
A.- Canviava les patates per una altra cosa, agafaven el que sigui i si deien que sí, ho canviaven..
X.- El català no l’escrivien com nosaltres, era diferent (és una informació del treball del seu grup)
Grup.- Els rals es deien també reials, hem estudiat les monedes dels segles XIX i XX.
N.- Una barra de pa valia un cèntim de pesseta
E.- Un cafè i una copeta valia 15 cèntims de ral. Un segell valia 8 cèntims.
T.- En quina moneda vàreu trobar els preus?
Nens.- De vegades en rals, de vegades en pessetes, de vegades en cèntims.

M.- Quan era la guerra a la meva àvia la van posar a la presó i tenia una filla petita i li havia de donar el pit. Per poder sortir va haver de donar el seu anell de casament.
Nens.- Per què estava a la presó?
M.- Era la guerra
N.- La meva àvia, quan tiraven bombes, es posaven tres sobre el llit i es tapaven amb un altre matalàs per si queia una bomba a la casa.
(Es desperta molt interès per les notícies de la guerra.)
T.- És molt interessant tot això que expliqueu.
Marta.- Si la meva àvia no s’hagués salvat, jo no hagués existit.

La tutora reorienta la participació dels nens cap a la problemàtica de la comparació entre les diferents unitats de monedes.Té intenció de fer arribar a la necessitat de reconvertir fàcilment un tipus de moneda en un altre i presentar el treball que havíem previst de confegir una taula amb les equivalències)

Tutora.- Veig que tenim preus amb rals, pessetes i cèntims. Què passa?
A.- Era una altra època
N.- Si una cosa val 10 pessetes i també val 15 pessetes potser és d’una època diferent.
N.- Potser compren a llocs diferents
Mestra.- Si l’E. diu que un cafè valia 10 rals i el P. diu que valia 10 cèntims o 10 pessetes, què ens passa aquí?
L.- S’assembla però ho està dient diferent: rals i cèntims
C.-Un parla de rals i l’altre de cèntims i són diferents monedes
X.-Els rals són més poc que les pessetes. Rals amb pessetes no comparem res
P.- En una pesseta hi ha quatre rals, és diferent, pot ser d’anys diferents
A.- L’E. potser d’abans, potser que l’avi de l’E. va néixer abans que l’avi del P.
Ll.- Els rals són més antics i en aquella època es valorava més. 10 pessetes seria molt.
An.- (aixeca la mà però quan la mestra li pregunta no sap què dir)
P.- Potser que l’E era el besavi.
P.- La gent tenia una moneda i després tenien rals i valien més, després la pesseta és més i ara l’euro és més.
E.-Els euros crec que valen menys que les pessetes. 10 euros en pessetes serien 20 pessetes per exemple. La pesseta és més
D.- Un euro són 166 pessetes
P.-Val més l’euro.
Una pregunta: dins una pesseta hi ha 100 cèntims i dins d’un euro?
Nens .- 100 cèntims
P.- És el mateix?
C.- En euros és més poc
T.- No ens posem d’acord sobre si un euro val més o menys que una pesseta , pensem una cosa que valgui un euro.
Nens: roba, un cotxe, mobles, una bossa de patates
T.- Anem a suposar que una bossa de patates i podeu preguntar quan val exactament.
(dibuixa dues bosses i escriu el preu a sota: 1 €). Quan val en pessetes?
N.- 166
Albert (mestre).- Podríem apuntar aquesta pregunta de la Paula i guardar-la per un altre dia.. “Si un euro té 100 cèntims i una pesseta també...valen igual?”

A.- (es mostra inquiet perquè vol intervenir). Marta, puc parlar ara?
T.- Ara parlarà el J. i després l’A.
J.- Se m’ha oblidat
A.- També podien canviar les coses per menjar
C.- Abans de les pessetes estaven els cèntims de pesseta.


Veiem com ara sí que la problemàtica se centra en el manteniment de les equivalències entre valors establerts i les diferents unitats de monedes: aquesta problemàtica es manifesta de diferents maneres:
- de vegades lligada a la numeració , com quan es confon el cardinal amb el valor com si les 166 ptes valen més que 1€)
- de vegades es refereix a la comprensió del sistema: dins una pesseta hi ha 100 cèntims, però dins d’un € també n’hi ha 100 de cèntims. Aleshores , valen igual els Euros i les pessetes?
- O al valor d’una bossa de patates (equivalència €-ptes?)
- O en les relacions entre rals i cèntims

LES PREVISIONS DIDÀCTIQUES DE LA MESTRA

Quan els mestres actuem professionalment també ho fem amb sentit i amb intenció. El fet que partim de les necessitats, idees , maneres de fer i converses dels nens i nenes no implica renunciar a les intencions educatives. I aquestes no només prenen un sentit ampli com el fet de desenvolupar idees pròpies, relacions amb la cultura, vinculació amb la història, etc. sinó que també pretenem desenvolupar el sentit i les relacions numèriques, la capacitat de càlcul, l’accés a mecanismes i tecnologia simbòlica elaborats per la nostra cultural, coses totes elles que permetin als nens i nenes inserir-se en la comunitat de calculadors de la que formen part, i ho facin amb més capacitat i més eines. Per això la mestra ha preparat una taula, que permeti als nens establir relacions d’equivalència entre rals, cèntims i pessetes d’una manera sistemàtica, i els permeti també anar descobrint les regularitats que estructuren aquestes equivalències. Però a la base de la seva proposta no hi ha només una intenció didàctica: hi ha present una problemàtica clara derivada de la necessitat que els nens de la classe desenvolupin més capacitat per establir relacions clares de comparació i equivalència entre els diferents preus que han anat trobant. Aquesta necessitat respon al fons del problema: Si una persona guanyava 20 rals durant una setmana, quant es gastava en les coses que necessitava per viure?

T.- Presenta el full amb la taula d’equivalències que hem preparat perquè facin
An.- Els cèntims amb els cèntims, els rals amb els rals, les pessetes amb les pessetes.
C.- Posarem ratlles al mig i 1 ral en cèntims, i en pessetes.
T.- Cadascú omple la taula com li sembli millor i si ho necessita pot agafar un paper per dibuixar o fer operacions. També pot agafar la calculadora o les fitxes o cubs apilables.

(Els alumnes passen a realitzar el treball. Els mestres ens distribuïm)
(l’A. em demana ajut. Amb la calculadora va calculant els cèntims però no ho pot fer autònomament perquè no sap les xifres de 25 ni 50 ni 75...També li costa molt usar la calculadora, molts cops ha de repetir perquè no interposa el signe + i el número se li posa a continuació de l’anterior. Per calcular les parts de pesseta ho fem amb els cubs però mostra una comprensió molt parcial.
La X. em demana la calculadora per calcular els cèntims però de seguida em diu que ja no la necessita que ja ha vist que sempre és igual: 25, 50, 75, 100, 125, 150, 175...).
A continuació mostrem alguns dels seus treballs

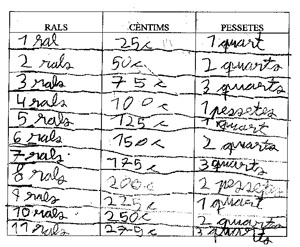
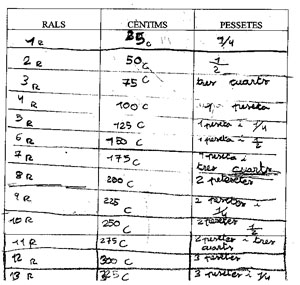
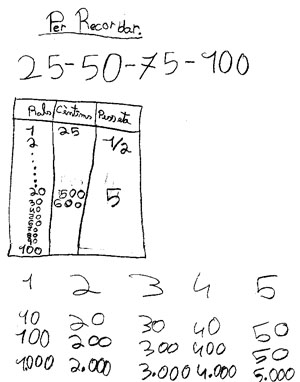
La primera cosa a valorar és el contingut sobre el que es treballa a l’ elaborar aquestes taules:
L’equivalència específica dels sistemes de numeració, per exemple entre enters i trencats, en el treball de la graella, on encara no els és evident que la podran utilitzar com una eina per saber els valor de les coses de l’època de Gaudí. A la graella, quant a aquesta idea de valor en relació a les equivalències numèriques, es treballen les idees i les dificultats de relacionar els valors de quantitats expressades en sistemes (numèrics, de monedes,...) diferents - Utilitzar l’estructura d’equivalència i proporcionalitat d’una taula de correspondència
- Comptatge amb la unitat 25
- Relació entre aquestes unitats i les fraccions, sigui utilitzant la unitat base (1 ral=1/4) com a generadora de noves quantitats, o sigui especialment en la comprensió dels trencats com a una relació part-tot, quan es pot passar de ¾ a 1 pesseta

Hem escollit diferents maneres d’estructurar la informació de la tercera columna, mantenint una mostra de la diversitat de les produccions

Veiem com en tots els casos la Taula s’utilitza com a eina de càlcul, basant-nos en la correspondència entre quantitats i en la consideració que les quantitats de la mateixa columna es van generant d’acord amb una regla específica que és diferent segons el patró que regula les relacions d’equivalència. En el cas dels cèntims el patró és el 25. Els nens , encara que amb errors com el cas de la C., poden aprendre les regularitats del sistema de numeració, comptant sense dificultats de 25 i 25, fixant-se en els coses que es repeteixen dins de cada centena. El comptatge de 25 en 25 (rals) ha fet descobrir a alguns nens i nenes les regularitats d’aquesta sèrie. El mateix es pot dir en el cas del comptatge d e les pessetes. És interessant valorar que, igual que passa en l’aprenentatge més sistemàtic i acadèmic de les fraccions, aquests nens utilitzen les equivalències entre sencers, mitjos i quarts, escollint un criteri per la seva elaboració. La majoria dels nens no són conscients des del primer moment que, per exemple 9/4, 2 1/4, 2 pesseta 1 quart, 2 ptes i 1/4 representen la mateixa quantitat de pessetes. Simplement estructuren el text de manera coherent amb l’opció d’escriptura que han pres, generant les quantitats posteriors a partir de les que tenen a sobre. És en l’espai de diàleg i conversa que es poden elaborar aquestes equivalències entre les diferents formes d’escriptura de la mateixa quantitat, per fer-les patrimoni de tots.

ELS TEXTOS DE LA MESTRA

En aquestes posades en comú, la mestra elabora, sovint amb la participació dels nens, textos que funcionen com a eina de reflexió, de posada en comú d’idees dels altres, com a element per a generar estratègies que puguin ser compartides, o com a síntesi i recordatori de coses que s’han verbalitzat a la classe. Que aquestes produccions no es converteixin en supletòries del pensament dels nens és una de les qüestions que hem d’estar més atents, ja que de cap manera la manera de fer d’uns ha de convertir-se en paradigmàtica suplint les maneres de fer dels altres, i restringint la manera pròpia de pensar.

REUNIÓ DE VALORACIÓ (Marta, Albert i Bea)

No ens hem de quedar només amb els mecanismes de càlcul. Ens interessa mantenir els vincles emocionals com a significadors del sentit profund del que fem:
- Tresor de les monedes
- Gaudí i la seva època
- Història personal
- Què necessiten les persones per viure
- Historia de les monedes


El càlcul és un mitjà. S’han plantejat dues qüestions:
- el valor dels diners, canviant
- les equivalències fixes entre monedes

Com seguir el càlcul?
- Consensuar la taula. Transparències de quatre maneres diferents de fer-la i que l’expliquin.
- Preparar cercles per anar omplint i visualitzar la relació part/tot.
- Provocar el comptatge de 25 en 25.

Proper dimecres : imaginar una família i les seves necessitats i els preus d’això. Primer col•lectivament i acabar el càlcul per grups.

20 rals setmanals era suficient per a viure una família?

La tutora recorda als nens que volen saber si 20 rals eren suficients a l’època d’en Gaudí per poder viure una família durant una setmana i proposa fer un llistat de les coses que necessiten.
Entre tots van dient el que pensen i la mestra va fent el llistat a la pissarra per capítols: menjar, roba, mobles... Aquest tipus de text obliga els nens a classificar les necessitats alhora que debaten sobre el que és o no necessari per a passar una setmana.

Durant la conversa van sortir alguns elements interessants, la majoria relacionats amb la possibilitat d’imaginar-se la vida de les persones en un passat llunyà i proper alhora: massa proper per pensar que potser no hi havia TV, massa llunyà per imaginar que els necessitats de mobilitat i transport no eren les d’ara…
Per això, aquests elements que sortien sobre la vida en el temps passat: viatges i transport , llenya-carbó, durada i ús de la roba, d’on treien l’aigua, els electrodomèstics (nevera /TV..) que tenien o no tenien, … són elements interessants i poden oferir vincles importants…

1.La decisió sobre els productes que una família necessita per a viure

Tutora.- Recordeu que havíem buscat preus de l’època d’en Gaudí per saber si una família en tindria prou per viure amb el que guanyava a la fàbrica.. Tenim el llistat de preus i ara intentem pensar què necessita una família.
N.- Menjar
Tutora.- Bé ara ja no direm més coses de menjar sinó d’altres tipus i després ja en parlarem de quines coses de menjar són necessàries. (Apunta menjar a la pissarra)
J.- Diners per comprar menjar
An.- (aixeca la mà però no respon)
P.- Roba
N.- Sabó
Tutora .- Com ho posem això del sabó (va fent el llistat a la pissarra)
N.- Dutxa o Bany
N.- Casa
M.- Una nevera
N.- La nevera va dins de la casa
Tutora.- La casa l’havien de pagar?
A.- Jo ho sé, si treballaven a la fabrica després li regalaven una casa.
Tutora.- Una altra cosa és el de dintre
N.- Electricitat
n.- Aigua
Ll.- Carro
L.- El cavall pel carro
N.- Llençols
Tutora.- Posarem les coses per la casa com a mobles
N.- L’aigua va amb la dutxa
A.- Els llibres per l’escola
Tutora.- Que els havien de comprar?
P.- Eren gratis
A.- Un pou
N.- Jo crec que no hi havia tele
M.- Sí però era sense colors
L.- Hi havia cine però era d’una altra manera
A .- Hort
Tutora.- Se’l compraven o se’l feien?
A.- Se’l feien i plantaven llavors i regaven
D.- Cotxe
G.- No és obligatori
Tutora.- (REPASSA EL LLISTAT)
- Casa, llibres i escola, no ho tindrem en compte perquè els ho donava la fàbrica.
- Carro i cavall ho havien de comprar cada setmana?
L.- No, perquè el cavall no es mor en un dia i es quedarien sense paga.
P.- El carro i el cavall no eren obligatoris perquè podien anar caminant per allà la Colònia Güell
A.- El carro l’han de comprar si es trenca.
T.- Menjar
E.- El menjar es gasta, no es compra per tota la vida
An.- Llenya perquè abans no tenien estufa
Tutora.- Roba, també dura per sempre?
P.- No, perquè si vas creixent la roba es queda petita.
R.- N’has de tenir per la primavera i per l’hivern i jo compraria una talla més gran
Tutora.- Ho hauríem de comprar cada setmana com el menjar?
N.- Cada mes

Amb aquestes intervencions es planteja la necessitat d’establir diferències entre el “grau de necessitat de cada producte”. Per això, la tutora proposa reflectir-ho amb diferent nombre de ratlles a cada fletxa (menjar,3 ratlles; roba,1; llenya, 4...)

Tutora.- Posarem tres ratlles a la fletxa del menjar i una a la roba.
C.- La roba et podria durar un o dos anys si no te la compres justa
Tutora.- Posaríeu més ratlles a la fletxa del menjar?
N.- Quatre o cinc
N.- Dutxa
A.- La tovallola
Tutora.- La posaríem amb la neteja o amb la roba?
Les coses de neteja quantes ratlles?
N.- Dues
P.- No, menys
Tutora.- (repeteix els motius de les ratlles posades fins ara i la P ho accepta)
N - Mobles
N.- Una fletxa més curteta que la roba.
Tutora.- Electricitat, aigua (pou), llenya... quantes ratlles posaríeu?
Adrià.- Quatre, perquè la llenya s’havia de comprar cada dia perquè es gastava molt ràpid
T.- Però la compraven o l’anaven a buscar?
N.- A buscar
Albert .- A part d’escalfar-se, per què més necessitaven la llenya?
N.- Per la barbacoa
Albert.- Per escalfar-se i per cuinar també, per fer bullir l’aigua. Algú sap una altra cosa que es feia servir per escalfar-se i cuinar?
A.- Carbó
A.- El carbó va més bé perquè les fustes poden estar humides o mullades si ha plogut.
Tutora.- L’An ja ho ha dit que poséssim moltes ratlles

Un cop confegit el llistat de necessitats, la tutora proposa repassar el llistat de preus que tenen i comprovar si falta algun apartat.

Ara llegiré el llistat que tenim de preus i si hi ha alguna cosa que no hem apuntat us queixeu.
Tutora.- Sabates
P.- No
N.- Sí, amb la roba
Tutora.- Posarem roba i calçat
D.- Una llauna de sardines, no.
N.- Són menjar
D.- La llauna, no
An.- Marta, una cosa, què és la cibada?
A.- Com la cançó

Altres qüestions interessants són les derivades de la categorització d’algunes necessitats: és l’oli un menjar? (menjar-beguda; menjar-aliment), i la seva codificació en funció de la seva durada i per tant, de si n’hem de comprar regularment…

N.- Oli
N.- És menjar
I.- És beguda
Tutora.- L’oli te’l beus?
I.- Tampoc te’l menges
O.- Amb la truita
N.- Per cuinar
Tutora.- Alcohol, què deu voler dir?
M.- Begudes que tenen alcohol
Tutora.- Posarem menjar i begudes
P.- La beguda es beu però també és un menjar
T.- Viatge curt amb tren
N.- Anirem en carro

2. Es passa a decidir el tipus de família que servirà per a realitzar l’estudi.

S’obre un debat sobre els avantatges de ser molts o pocs fills. Des del punt de vista econòmic s’arriba a la conclusió que si bé una família amb més membres té més necessitats, també té més ingressos quan els fills ja treballen. Per prendre la decisió es té present el tipus de família de l’època, amb més fills que en l’actualitat (pares , tres filles i tres fills)

Tutora.- Ja tenim coses de tot. Ara anem a imaginar-nos quina mena de família era.
Grup.- Pare, Mare, un fill i una filla
R.- Jo vull dir una cosa d’això d’abans: ja sé perquè es cremava més ràpid el carbó, perquè era llenya cremada.
Tutora- D’on aconseguien el carbó?
R.- Dels arbres
A.- De les mines
Albert.- A lo millor surt de diferents llocs, a lo millor no tot és igual, ho podríem apuntar per un altre dia.
(continua el tema de la família)
Tutora.- l’I. diu que no, per què?
I.- Podrien ser més
J.- Ja està bé amb dos perquè quan estic a casa la meva germana no para d’empipar-me
An.- Un i un perquè no es barallin
J.- Perquè si són molts necessitarien molts diners
P.- Millor dos i dos perquè no juguen tan sols
Tutora.- Algú creu que la gent d’aquella època tenia més fills? Penseu en les fotos.
P.- La meva àvia tenia cinc fills i la gent en tenia molts
R.- A l’època del Gaudí va viure el pare del meu pare i saps quants fills tenia? amb el meu pare, tretze
M.-La meva tieta tenia sis fills
P.- Vaig llegir en un llibre que fa anys a un altre país una senyora va tenir 69 fills
E.- Si són més necessiten més menjar però també poden treballar més gent i guanyar més diners
P.-. (Proposa) Tres fills i tres filles
T.- Què més ens queda per fer?
J.- Saber els diners que guanyaven a la fàbrica i què necessitaven per menjar.

Amb aquests criteris es proposa fer l’estudi per grups de tres alumnes, triats lliurement “per poder treballar bé”

Tutora.- Ho fareu per grups de tres persones que pugueu treballar bé
C.- I l’edat dels nens? perquè si eren petits...
S.- Allò que has dit dels grups, potser n’hi haurà un de quatre

La sessió ha estat plena d’interès per als alumnes que en tot moment han participat molt activament. No hi va haver temps suficient per acabar i molts grups van mostrar un sentiment de contrarietat per no poder continuar treballant.

Quan entrem a valorar el treball proposat, veiem que es tracta d’UNA SITUACIÓ MOLT COMPLEXA, ja que afecta a molt elements de caràcter social i de caràcter matemàtic que es presenten alhora i s’impliquen mútuament. Els referents personals i la comparació amb l’actualitat, han estat el punt de partida per poder comprendre la manera de viure en aquella època: les necessitats de les persones, “la família ideal” per a cadascú, les històries que coneixem dels avis. Els aspectes matemàtics formen part de tota aquesta complexitat com una eina que ens ajuda a comprendre millor determinats aspectes d’aquella època.

Analitzant el treball dels diferents grups es detecta la història del procés seguit, les dificultats, idees posades en joc.

1

2

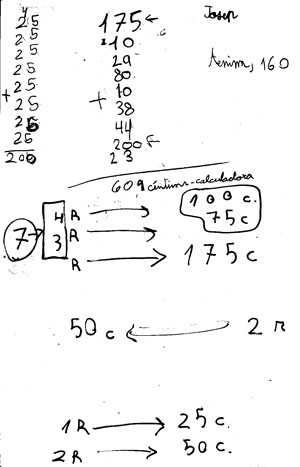
2

3

4

5

6

7

8

9

ANÀLISI D’ALGUNS ELEMENTS D’AQUESTA COMPLEXITAT

En la situació que s’ha estat treballant, hi són presents com ja hem assenyalat molts components de caràcter ben diferent: les necessitats de manutenció, el temps de la història, els preus de les coses i el sentit de valor, la maneres de viure i les prioritats de les persones, etc. I també altres elements de caràcter matemàtic com la correspondència, la proporcionalitat, les relacions entre addició i multiplicació, i/o els simbolismes, anotacions, maneres de representar quantitats, preus, el sistema de monedes, etc. A més, com a element central i determinant hi són els elements emocionals de la situació, que ja han estat abastament comentats, així com els derivats de la gestió de la tasca: la comprensió del treball a realitzar, els acords de grup i els rols de cadascú, el temps disponible, etc.

Tots aquests i altres elements han estat presents en el moment de realitzar aquest treball, de valorar les opcions que s’anaven prenent, d’argumentar i escollir possibilitats diferents.

A continuació explicitem alguns dels elements que han format part de la complexitat d’aquest treball, sense necessitat d’entrar a valorar el sentit i caràcter de les respostes dels nens i nenes.

1. ELEMENTS DEL CONTEXT

1.1.Definir la unitat familiar (2): era el problema d’imaginar quina família era la més habitual en l’època: aspectes de nombre de fills/es, la composició de la família (en un grup sortien avis), d’edat dels diferents components, que serà determinant per la relació entre guanys salarials i necessitats de manutenció.

Després de les primeres valoracions sobre això, es pren un acord col•lectiu, amb tres fills i tres filles , sense avis (ex:2, 5). Això facilitarà el treball dels grups i la posterior posada en comú sobre despeses, tot i que potser es podia haver deixat a la decisió final de cada grup.

1.2. Els guanys de la unitat familiar:
En el marc d’aquesta família, cada grup havia de definir el nombre de persones que treballarien, i si tenien o no el mateix sou.
Són interessants les opcions dels diferents grups i valorar en funció de quins criteris actuen : Per exemple: només treballen els mascles? Els nens petits treballen? Cobren igual? Exemples: 2, 3, 4, 5, 6, 7, 8

1.3. Definir les necessitats setmanals de la família (1). Es presenten al menys tres qüestions importants sobre les que han de prendre decisions:

- Atribuir i definir i categoritzar el que és necessari o no. Implica en el grup una decisió conjunta sobre temes com per exemple: l’oli és un menjar? Cal un cavall i un carro per família? Per a això han d’estar disponibles una sèrie de coneixements i a més han de poder “veure” l’època de’n Gaudí intentant-se separar de la seva mirada actual (1 família, ara, disposa d’un cotxe, o elements subjectius com per exempleo “a mi no m’agraden les sardines”… doncs no posen sardines) - El que es defineix com a necessari: és suficient? Es refereix a la dificultat d’imaginar les quantitats de menjar que consumirien 8 persones en 7 dies.
- Dependència de la llista prèvia en fer el llistat de necessitats. Aquesta dependència era:
- respecte dels productes: tots eren de la llista
- els criteris que han utilitzat per fer la llista: agafar-la tota, imaginar el que els agrada…
- en el cas d’alguns grups, respecte de les quantitats que la llista assenyalava prèviament (1ou- o 8 ous) Exemples 3, 9

2. ELEMENTS MATEMÀTICS DE LA MESURA I EL CÀLCUL

2.1.Establir relacions entre preu unitari (1 ou val...) i preu total (8 ous valen...)
.Les seves respostes estaven en funció de si s’havien adonat del canvi de context, i poder valorar que el preu del producte ja no seria el del llistat sinó que implicaria un canvi i una necessitat de calcular d’acord amb el nombre de membres de la família (per a nosaltres una multiplicació-proporció).
Si se n’adonaven, com resolen aquests càlculs?
Ex: 1, 2, 3, 4

2.2. Establir relacions entre les diferents unitats del sistema de monedes
- Havien d’adonar-se per exemple que uns preus estaven en rals, altres eren cèntims i altres estaven en pessetes, i que aquesta diferència era important. Veure com l’exemple 8 transforma tots els preus en pessetes…
- Adonar-se que els sous estaven en rals i els preus en cèntims (o…) i que això afectaria al judici de si és suficient per viure (veure cas del grup 2).
- Valorar els recursos i els mecanismes de conversió i càlcul que utilitzaven per resoldre aquests problemes. Per exemple: com utilitzaven la taula 1 o la taula 2 (consensuada el 21/1) Ex: 2, 6, 7, 8, 9

2.3.Utilitzar diferents estratègies i mecanismes de càlcul:
Podem veure les següents:

- Estratègies multiplicatives o sumatives, Ex. 1, 8
- Tendència a buscar un algoritme estandarditzat, Ex: 1, 4
- Càlcul per unitats compostes. Ex: 2, 8
- Càlculs amb el cap, amb paper i llapis, amb la calculadora…Ex: 1, 6
- Utilització de sistemes per controlar el seu càlcul. Ex: 2, 3, 8

Els nens i nenes durant la setmana han estat treballant per grups per acabar els càlculs de la sessió anterior sobre si “En tenien prou les famílies per viure amb els diners que guanyaven a la fàbrica?” i s’han preparat per poder explicar els seus treballs amb transparències a la resta d’alumnes. La consigna ha estat “qualsevol membre del grup ho ha de poder explicar”.

Ha estat molt important la capacitat dels nens d’estar tanta estona centrats en una tasca. Era inevitable que alguns de tant en tant desconnectessin, però la implicació era permanent en el conjunt de la classe, generant-se preguntes, propostes, idees, hipòtesis …contínuament. La qüestió és que en un procés així s’obren moltes portes i de vegades costa posar-hi una mica d’ordre, cosa que necessitem per poder continuar treballant i ajudar als nens i nenes a organitzar les idees que es van manifestant, fins a poder sistematitzar algunes qüestions.

Durant la presentació ens interessava estar atents a les següents qüestions:

- L’adequació al context : per exemple, si la relació entre el menjar planificat i les necessitats per viure era l’adient. Ens interessava que, a partir del contrast entre les propostes dels diferents grups i les seves pròpies valoracions fossin capaços d’avaluar les seves propostes inicials i intentar respondre a la pregunta prèvia: “En tenien prou?”. És molt interessant valorar les opcions que prenen, en funció de per què les prenen i com, sovint canvien les seves decisions en funció de l’adequació de la resposta als seus coneixements de tipus social o de caràcter matemàtic. El que ens interessava no era tant si milloraven i refeien els seus treballs com el fet d’adonar-se dels problemes que se’ls presentaven.

- Valorar quins han estat els criteris que els han determinat més en el moment de prendre decisions: els relacionats amb els càlculs, com per exemple la facilitat en els càlculs o la utilització d’unes dades o unes altres com a eix del càlcul (els diners en el cas de l’E.) o les persones que composaven la família, com per exemple quines treballaven i què aportaven …

- Quina influència pot haver tingut la documentació que es va utilitzar per elaborar el llistat de preus (una part important va ser una taula del llibre de text de l’ESO):
la seva estructura, la informació que contenia, la informació que ens interessava
recollir, la relació entre els preus del llistat disponible i les característiques de la
situació a decidir.

Utilitzarem diferents moments de la devolució per centrar-nos en algunes de les qüestions que han estat més interessants i ens han servir per reflexionar conjuntament. En alguns casos les reflexions que fem posteriorment es refereixen a aspectes que ja s’han comentat en l’apartat de la sessió anterior, centrada en la complexitat.

En tenien prou les famílies per viure amb els diners que guanyaven a la fàbrica?

A.- (en veure l’Albert) No li hem tornat a l’Albert les seves monedes
Tutora.- Sí, li vaig tornar l’altre dia
Albert.- Ja li vaig tornar a la senyora velleta i ja està tranquil•la perquè eren els records de la seva vida, tot i que confiava que vosaltres ho cuidaríeu molt.
A.- Marta, quantes ulleres tens? ... On vius?...
Tutora.- (Respon ràpidament i passa a presentar la sessió)
Posarem les transparències perquè els grups puguin explicar. Tothom del grup ha de poder explicar el que va fer. No cal explicar-ho tot.
Quina era la pregunta que volíem saber?
Grup.- Quant guanyava una família
T.- Sí, i si en tenien prou per a la setmana.

GRUP 1
O.- Vam ficar: germà gran, petit i mitjà. Guanyaven 60 rals
R.-I vam decidir que necessitàvem més diners per poder comprar altres coses com roba i vam posar a tota la família a treballar i guanyaven 180 rals
J.- Nosaltres ho vàrem comptar i tots vuit guanyaven 160 rals
R.- No, perquè nosaltres ho vam fer amb la calculadora, potser vosaltres ho vàreu comptar en euros.
Albert.- Què vàreu pensar? 8 persones a 20 rals cadascuna? Era això? Algú sap una manera ràpida de fer-ho?
N.- Multiplicant.
N.- Jo ho vaig fer sumant.
Albert.- També es pot fer sumant.
Qui ho sap fer amb la calculadora multiplicant?
L.- Jo. El 20, la X vol dir multiplicar, el 20, la X, el 20...
C .- No, el 20 la X i el 8...160
R.- Nosaltres guanyàvem 180
Albert.- Perquè havíeu comptat una mica més de 20
(El R. no ho té clar)
J.- Els pares guanyaven 80 i els petits 20 rals
R.- Ara ja no val el 160.
Tutora.- Rectifica-ho amb el retolador
C .- Jo vaig fer el càlcul i gastaven 81
R.- Què dius? Després vàrem ficar més coses i gastaven 99
Tutora.- Què havíeu posat que gastaven
(llegeixen el llistat)
Tutora.- Com ho vau pensar que en 1 setmana necessitaven això? Ja no ho recordeu? Bé que surti el grup del J. que diu que ho recorda.

1. QÜESTIONS RELACIONADES AMB PROBLEMÀTIQUES SOCIALS
Com es pot veure, les seves decisions han estat determinades per valoracions que, abans que a les matemàtiques, impliquen a qüestions que tenen a veure amb els modes de vida. Com per exemple:

1.1.Decisions per determinar qui treballava:

- La percepció que tenen de la relació entre les necessitats de compra i el capital que necessiten per comprar-ho: per exemple, si pensaven que no en tindrien prou poden canviar la decisió inicial i dir que també treballen els nens:” per tenir més diners”

- Una altra solució que alguns grups es plantegen son les diferències de setmanada entre adults i nens. Alguns grups disposen d’aquesta informació (que els nens cobraven menys que els adults) i altres no, però no tots els que en disposen la utilitzen a la seva conveniència. Per això en R. diu: ”Ara ja no val el 160”

1.2.Decisions en relació a què comprar:

- Quan creuen que després d’un primer llistat encara els sobren diners, alguns prenen la decisió d’ afegir més coses, verbalitzant o no l’argument que potser era poc menjar el previst inicialment.

- Si creuen que algun menjar és massa car (pollastre), diuen que no en compren sinó que compraran coses més barates (bacallà)

- Alguns grups valoren que no es compra el mateix cada setmana. Un ho fa dient que hi ha productes com la roba o el calçat que no cal adquirir-los setmanalment, però que cal deixar diners. Un altre ho fa amb el criteri que no cada setmana es menja el mateix

- Surt el problema que si no compren suficient d’un menjar per a tots, seria un embolic ja que menjarien coses diferents i… ¿Com es repartiran el menjar si no en tenen prou d’un mateix producte per a tots els membres de la família?.

- Un grup diu que compren una determinada quantitat i després ja aniran agafant el que els calgui per anar menjant fins que s’acabi

- Un grup intenta organitzar la compra en despeses repartides per a les 3 menjades de cada dia de la setmana, però no acaben…

1.3.Decisions sobre si amb el que han proposat comprar en tenen prou o no:

- Un grup, davant la sensació que els faltaran diners, “s’inventen” la idea que a la fàbrica els donaran el dinar gratis, i només han de comprar sopar i esmorzar

1.4. Altres problemàtiques:

- Qui es queda a casa per tenir cura dels petits si treballen pare i mare?
- “Ens agradaria treballar des de petits?”: Aquí es genera una discussió sobre si ells voldrien treballar o no: quins avantatges tindria (tenir diners, ser gran?) i quins inconvenients
- Anacronismes, com que si arriben cansats a casa es dutxarien, s’estirarien al sofà…

GRUP 2
J.-1er dia, vam posar 8 ous.
2on dia, el X va dir que a la fàbrica ja els donaven de menjar i per sopar ja en tenien prou
Tutora.- Tu, X. ho sabies això?
X.- Ho vàrem suposar.
Tutora.- Quant guanyaven?
N.- 160
E.- (Explica el càlcul que van fer. Van associar els 20 de dos en dos, després els 40, després els 80, i al final els dos 80.
Albert.- Com ho saps que 80 i 80 fan 160
E.- 8 i 8 fan 16 i li poso un 0 al darrera. (1)
Albert.- Aquí tenim una família que guanya 160...160 pessetes?...160 cèntims?...160 rals!
...I van a comprar 7 quilos de pa ...dieu que són 25 cèntims. Què posava el llistat? 1 quilo val 25 cèntims, que és un ral. Quin problema hi ha aquí?
E.- 25 cèntims és igual que 1 ral; 7 quilos, 7 rals
Albert .- (repeteix el que ha dit l’E.). P, ho vols explicar tu?
P.- Jo crec que valen 7 rals perquè si diuen 1 quilo val 25 cèntims que és igual que un ral, 7 quilos valen 7 rals (2)
Tutora.- Posa que 8 ous valen 80 cèntims, és veritat o no? Què diu el llistat : 1 ou val 10 cèntims
2....20; 3...30; 4...40;5...50;6...60;7...70;8...80. Molt bé
Albert.- 8 llaunes de sardines...200 cèntims. Com ho sabeu? Què posava el llistat?...1 llauna ...25 cèntims.
Quantes llaunes?. Mirem la suma de la transparència: 25+ 25...8 vegades
Estan les llaunes aquí? Les veieu?
Heu pensat molt
N.- La suma de tot dóna 609 cèntims però no ho vam tenir temps d’acabar perquè ens vam “liar” amb la calculadora per passar-ho a cèntims
(expliquen que van començar a passar 175 cèntims, que era la primera quantitat de la suma i volien fer 25 vegades 175)
Albert.- Què és el 175?
N.- Cèntims .
Albert.- 1 ral són 25 cèntims i 25 cèntims quants rals són? (3)
Grup. –Un
Tutora.- És el mateix 25 cèntims i un ral
Grup.- Sí
Tutora.- 50 cèntims quants rals són?
Grup.- 2
Tutora.- I 175 cèntims
L.- 3 rals. Ho sé
P.- Fem el 75 i després el 100
L.-100 són 4
(L’Albert va fent la taula a la pissarra)
L.- Ho ajuntem el 100 i el 75
D.- 4 i 3 són 7 rals (1,3,4)
(Albert completa la taula 175c...7 r)
Tutora.- Es el mateix que feien ells...175 i 175 i 175...?
Algú els diu en què s’han equivocat?
An.- Un número és més gran i l’altre més petit
L.- S’han equivocat al sumar
P.- Volien passar de cèntims a rals i no es fa la suma, la suma és una altra cosa i l’altra els cèntims i els rals.
A.- Igual que al meu grup sumaven cèntims i rals (5)
J.- No això no ens ha passat, tot eren cèntims.
Albert.- El vostre problema crec que era que no podíeu comparar perquè el que gastaven ho teníeu en cèntims i el que guanyaven en rals.
Calia fer-ho (passar a rals) cada vegada de cada quantitat de la suma o ho podem fer passant només el resultat?
N.- No
P.- Podem passar els rals de la suma i tindrem els rals de tot
N.- Jo no ho entenc
Albert.- Ho anem pensant perquè el més important era saber si podien viure o no

GRUP 4
I.- Primer vam decidir la família i quant guanyaven
Tutora.- Per què poseu que 3 pollastres valen 48 rals?
I.- Un valia 16, vam sumar tres 16 i era 48
1 ou ...10 però no potser un ou perquè els altres...
An.- No podrien menjar!
(han fet sumes per calcular 8 vegades el 10, 10 vegades el 10 i s’havien equivocat: 110. La tutora els fa comptar mentalment)
Tutora.- Per què vàreu escriure les sumes si ho sabíeu comptar de cap?
I.- Per si ho havíem d’explicar...
E.- Qui s’encarregava dels petits si el pare i la mare treballaven, qui els duia a l’escola i els recollia?
Tutora.- Per què ho dius? El teu grup va deixar algú de gran a casa per tenir cura dels petits?
Didac.- La mare a casa fent de mestressa de casa
Irene.- 1 litre de vi 10 cèntims, 10 litres 110. La Gemma no estava d’acord, deia que era 100 , però ho vàrem fer amb la calculadora.
T.- Ho comptem? 10, 20...100. Ho hem fet millor amb el cap que amb la calculadora

2. QÜESTIONS RELACIONADES AMB LA MATEMÀTICA

Veiem com cada cop més han sorgint qüestions que es relacionen directament amb les matemàtiques i el càlcul.

Aquestes qüestions giren principalment al voltant de la problemàtica de la multiplicació, en situacions i aspectes diferents:

Les situacions són:

- La que es refereix a la relació entre preu unitari d’un producte i preu total. No tots els grups se l’han plantejada conscientment , però per a tots es fa evident després de la devolució que alguns grups han fet del seu treball.(2). Són situacions que representen la utilització de la proporcionalitat simple que tan bé expressa la Paula i abans l’Ernest

- La que té a veure amb les relacions d’equivalència entre els valors de les diferents unitats del sistema de monedes. (3, 5) Aquesta problemàtica es relaciona amb:
• Com poden comparar quantitats expressades en diferents monedes (rals-cèntims…)
• Com poden transformar-les?
• Com podríem utilitzar la multiplicació per fer això?

Les dificultats més grans s’han manifestat en la segona situació.
En la primera , un cop explicitada, no semblava implicar tant a problemes de comprensió, com alguns problemes de càlcul. Així, segurament la relació : “si hi ha 8 ous, necessitarem 8 vegades el que val 1 ou” els és més evident. És una relació de proporcionalitat directa, molt propera a contextos coneguts per ells en l’actualitat.

En canvi , en la segona situació, els problemes es manifestaven degut a qüestions com les següents :
- Ells havien transformat rals en cèntims: és una proporcionalitat directa, calculant de 25 en 25 (no amb la idea de multiplicar). En canvi, al fer al revés, com passar de cèntims a rals, la proporcionalitat és inversa, i la manca de pensament reversible dificulta la seva comprensió, i així, actuen amb el mateix criteri: comptar 25 vegades (en aquest cas 25 vegades 175 cèntims)
- El fet de no tenir una vivència directa de rals i cèntims. Per això, encara més veuen aquestes monedes com a coses
diferents, no com a parts d’un mateix sistema en què les equivalències mútues són essencials.
- La dificultat d’utilitzar la taula com a mecanisme de càlcul. En alguns casos aquesta dificultat pot ser un problema de conceptualització ( de la consciència que la taula expressa aquestes equivalències), però en la majoria de casos és més un problema derivat de com trobar maneres per poder composar valors diferents dels expressats explícitament a la taula ja que per fer això els cal utilitzar la composició entre alguns d’aquests valors explicitats.(4)

Segons el que s’ha assenyalat sorgeixen diferents aspectes referits a les següents qüestions:

- A la comprensió reversible de les relacions d’equivalència
- A la manera com entenen la multiplicació: si la veuen com a una operació en què intervenen dues magnituds diferents i si són capaços de tenir-les presents quan calculen
- A la reversibilitats dels càlculs i el que això implica al calcular

I com una problemàtica profunda que relaciona els aspectes matemàtics amb els socials: ¿Com podem comparar de manera fiable, és a dir sense perdre la qualitat dels valors, el que cobren i el que gasten, mantenint el valor de la realitat si aquests valors expressen unitats diferents?
És a dir:
- Poden veure que per tal de donar resposta a la pregunta (“en tenen prou?”) s’han de comparar les dues quantitats i que per valorar quina és més gran, han de prendre en consideració no el valor absolut del nombre sinó el relatiu a la moneda? - Poden veure que per a fer això és necessari que puguin reduir els valors a una mateixa unitat?(5)
Alguns grups ho manifestaven i altres no.

Els mecanismes de càlcul utilitzats en la multiplicació:

Una de les qüestions que vam poder valorar és la dependència que EN UN CONXTEXT TAN COMPLEX, els nens encara tenien de la suma:
- La majoria encara sumava utilitzant unitats simples.
- Pocs nens accedeixen a la necessitat d’agrupar en unitats compostes, cosa que significaria una tendència a la multiplicació
- Tampoc expressen que d’alguna manera estan multiplicant, i que hi ha maneres diferents i especials de multiplicar (5) - Alguns utilitzen la calculadora per multiplicar, però ho fan com si la multiplicació fos un signe, i així usen com a addició repetida: la multiplicació no integra un seguit de sumes, per dir-ho així…

Altres problemàtiques matemàtiques:

- Es veu una tendència massa gran a l’algoritització formal, i com que només coneixen la suma, a sumar.

- La no comprensió que l’addició implica la reunió de tots els valors sumats, i que no cal convertir a rals el valor expressat en cèntims per cada sumand, si podem fer-ho directament de la suma total.

Afegim, a continuació, part de les converses dels altres grups, sense entrar en més detalls ni anàlisis

GRUP 3
M.- Primer vam pensar quantes persones podien treballar en la família.
(Han recollit el seu procés en forma de pregunta-resposta. La M. va explicant i llegint i la P. va assenyalant la transparència. Després la P. explica i li passa el llapis per assenyalar a la M.)
-P.- No compren el mateix cada setmana, sempre no necessitaven sabates o roba. Ho pensem i ho sumem
C.- Hauríeu d’haver fet dos llistats: el de les coses que compraven cada setmana i el que no
(An. i X .i descansen el cap damunt la taula. L’An. quiet, d’esquena a la pantalla, el X. de tant en tant el toca)
M.- Vam tenir un problema, que ho vam sumar amb la calculadora però vam barrejar cèntims, pessetes i rals
Tutora.- Què hauríeu de fer?
X.- Nosaltres no som genis
Tutora.- I què faríeu si fóssiu genis
Grup.- Passar (aquí els nens expressen clarament com viuen la dificultat de “passar”, de convertir les diferents unitats...)
P.- Jo els vaig dir que ho passessin a cèntims
Grup.- Només teníem 16 rals i 1 pesseta, la resta eren cèntims... Vam fer quants rals eren 378 cèntims a la taula
Tutora- I ho posava el 378?
N.- Sí
Tutora.- Mentre ho busqueu surt un altre grup

GRUP 5

D.-(explica el tipus de família: l’edat dels nens)
D.- (Es sorprèn) I els pares, no hi són?
Tutora.- Per què ens importava saber l’edat dels fills i no la dels pares?
Ls.- Perquè els pares són grans i treballen, però els fills depèn de l’edat
L.- Guanyaven 280 rals . Ho vàrem pensar i després amb la calculadora ens va donar el mateix.
Ls.- Vam pensar què necessitaven per la setmana, i vam continuar fins a l’altra setmana, perquè no sempre era el mateix.
Tutora.- Quant gasten?
1303c.......32 r........1,95 p (han sumat per separat les tres monedes)
Tutora.- Sabem si en tenen prou o no?
Ls. -Jo crec que no perquè hi ha 1303 cèntims i només guanyen 280 rals.
L.- Però són rals i cèntims
Grup.- No perquè una cosa està en rals i l’altra en cèntims
Tutora.- Ens serveix per saber si en tenen prou o no?
Grup.- No
Tutora.- Us ha passat com als altres grups

GRUP 6.-
C.- (Explica el llistat) Compraven per la setmana i cada dia agafaven el que necessitaven.
Gastaven 634 cèntims en una setmana
Albert.- Perquè poseu que 1,50 pessetes són 150 cèntims?
A.- 100 c eren 1 p, 150......1’5(?)
Guanyen 140 rals
Tutora.- En tenien prou?
C.- Vam tenir problemes perquè confoníem la coma de la calculadora amb el puntet del mil.
Jo crec que en tenien prou i de sobra.

(S’acaba el temps, després del pati continuen i dues secretàries prenen apunts) Una de les qüestions que ens plantegem és en quina mesura la complexitat de la tasca que s’estava realitzant, les diferents coses que havien de tenir en compte, les decisions que havien d’anar prenent al llarg de tot el procés, podia haver implicat una menor atenció al que serien els aspectes matemàtics, i tenir repercussions en la conceptualització dels càlculs i els mecanismes utilitzats en els diferents moments. Això ens fa reflexionar sobre la manera com es podria continuar, com avançar algunes qüestions més generals, com la multiplicació, que poden ser objecte més directe de la nostra atenció.

Què és més: el que guanyen o el que gasten

Després de les valoracions sobre la sessió anterior, vam valorar la conveniència de reduir la complexitat de la situació centrant-los en un dels problemes matemàtics especificats: el de les relacions d’equivalència dins del sistema de mesures.
En aquesta sessió es va proposar recollir les propostes finals de cada grup i retornar-les globalment com una situació a resoldre : “En cada família, què és més: el que guanyen o el que gasten”.

La intenció que teníem era que la sessió aportés uns models que visualitzessin les relacions entre els diferents valors d’un sistema de mesures i facilités als nens i nenes l’estructuració de la situació mitjançant les matemàtiques, Per a això, caldria, entre altres coses millorar el sentit dels nombres i les operacions implicats i establir relacions entre ells, principalment mitjançant les relacions multiplicatives, que ens semblaven lluny encara del seu pensament, al menys respecte d’aquesta problemàtica concreta.

Per abordar aquest problema calia, en primer lloc, que adquirissin la consciència sobre la necessitat de reduir els valors a una mateixa unitat, i una decisió també conscient sobre a quina unitat es podia reduir , i per tant sobre els criteris que permeten imaginar quina era la unitat de conversió més útil, o quina era més fàcil.

Una altra problemàtica relacionada amb aquest treball, és la dels recursos i mecanismes de càlcul:
Per això, des del principi se’ls va donar una taula de conversió semblant a la que ells van construir. Calia ajudar-los a imaginar maneres d’utilitzar-la.

REGISTRE DE LA SESSIÓ

(Participem tres adults: Marta (tutora, que dirigeix el grup), Albert (assessor, que observa i intervé) i Bea (mestra suport, que observa i registra) (Tres dels alumnes: A., An, i X. estan considerats necessitats d’una ACI a l’àrea de matemàtiques)

Tutora.- Ahir vàreu estar treballant per grups per contestar unes preguntes. Qui les pot recordar?
I.- Quantes persones treballaven a la família, quant guanyaven .
Tutora.- (Repeteix el que ha dit la I.)...i quant necessitaven per viure i si en tenien prou.
Ho vam apuntar de tots els grups i el D. em va ajudar a passar-ho a l’ordinador.
Tenim de tots els grups quant guanyava i quant gastava la família que vàreu triar, excepte un grup que no ho havia acabat.
R.- Al nostre treball hi ha un canvi que vàrem fer al final.
Tutora.- Sí, ja ens vàrem adonar i ho vam posar.
Ara sabem quant guanyaven i quant gastaven, què podríem saber ja?
A.- Si en tenien prou
X.- Per passar la setmana.
An- Ahir el Ricard em va dir que no era el meu amic.
Tutora.- Després ho parlarem.
R.- A nosaltres ens sobraven diners per a l’altra setmana.
Tutora.- Què podien fer si els sobrava.
E.- Guardar-ho per la setmana vinent
C. - Estalviar-ho per quan necessitin alguna cosa com per exemple si se’ls trenca el llit.
N.- Per si estan malalts
P.- Per a la farmàcia.

Veiem la manera com la tutora es planteja la necessitat de reelaborar i actualitzar un problema que era pendent. Aquesta és una acció pedagògica bàsica, que no podem donar per suposada. (La Tutora reparteix un full on hi ha els resultats dels diferents grups i la taula de reconversió que ha preparat l’Albert)

Full resum de despeses-guanys

Tutora.- Poseu el nom i la data
J.- “Esto no lo entiendo yo” (1/4: es refereix a la taula d’equivalències que es mostra més endavant)
Albert.- Abans de començar a mirar si en tenen prou o no, mirarem primer el full. Anem a veure aquest número que van escriure el grup del J., el Ls. i l’E. (321,303)
Jo l’escric i mirarem si el podem entendre.
Ls.- Jo crec que són 32 rals i 1.303 cèntims.
Albert.- És que la calculadora posa el punt del mil a dalt i no hi estem acostumats.
Ls.- Com que a l’altre costat hi ha els rals que guanyen ja ho podem comparar!
Albert.- (escriu a la pissarra)

Guanyen: 280 rals // Gasten: 32 rals 1.303 cèntims

N’hi ha prou per comparar?
Ls.- Sí: un és mitjà, l’altre gran i l’altre petit. El gran té més números.
Albert.- I tu, P. creus que el que té més números és més gran?
P.- No. Posa-li un tres al davant (3280), ara tenen els dos quatre números però un té un tres al davant i l’altre un ú.
Albert.- Però les coses que comparem són de la mateixa categoria, els cèntims i els rals?
Imagina’t que comparem
1 milió € 1000 €
Imagineu que us donen a triar

Ls.- És el mateix
Albert.- Qui sap escriure un milió en números?
R.- (escriu 1.000.000)
J.- És el mateix
Albert.- Hi esteu d’acord?
Grup.- No, un milió és més
Albert.- No s’ha de mirar només el número sinó el que és.

Es comença a treballar col•lectivament per analitzar algunes dades que no es comprenen.
Busquem col•lectivament la solució i apareixen tot un seguit de qüestions:
Com comparar dades expressades en unitats diferents? Necessitat de convertir una d’elles en la mateixa unitat monetària que l’altra.
- a)321,303: S’arriba a la conclusió que són 32 rals i 1.303 cèntims i que ha estat un problema en l’ús de la calculadora que posa el punt a dalt i no hi estem acostumats
- b) 6,14 cèntims: S’arriba a la conclusió que ha de dir 6,14 pessetes, igual que escrivim 6,14 €

T. Què podríem fer per saber si guanyen prou o no?.
E.- Multiplicar
C.- Mirar la taula.

Per ajudar-nos a calcular el que vulguem dels preus d’aquella època (1852-1926), vam fer una taula com aquesta:

Albert.- I com?
P.- Jo primer buscaria els cèntims a la fila dels cèntims
Nens.- No surt!
Una de les dificultats que es fan més paleses és com, al moment d’usar la taula, s’ han de buscar quantitats que no estan expressades directament en ella (per exemple 88 rals), i ho haurien de fer per composició o descomposició entre d’altres que sí que hi són. Posteriorment s’hauria de fer el càlcul del total un cop esbrinat el valor equivalent de cada part; es pot optar per l’arrodoniment, desestimant algunes quantitats irrellevants per al resultat. Han de tenir clares les correspondència entre les diferents columnes i el valor qualitatiu de cada una de les columnes.

Albert.- Anem a poc a poc i si ens anem ajudant segur que ho entén tothom..
P.- Hem de passar els cèntims a rals i afegir els rals
Albert.- Enteneu el que diu la Paula?
N.- No
Albert.- Tu, P. dius que mirem el 1.303 a la fila dels cèntims per saber quants rals són
S.- Hi ha una cosa que no entenc... com parla tan fluix.
P..- T’has de fixar en el 1.303. El primer és mirar a la taula quants rals són.
Albert.- Per què penseu que la Paula vol saber quants rals són?
J.- Perquè si no , no podem calcular perquè no és el mateix cèntims que rals.
Albert.- Farem una trampa, com que els cèntims valen poquet en comptes del tres posarem un zero (1300)
Busquem primer el 1000 i després quants rals són
J.- 40
Albert.- (Encercla l’1 de 1300 i fa una fletxa que diu 40 r)
I el 300, qui el sap buscar?
J. i altres.- 12
Jo..- Ara hem de calcular el 40 i el 12
Albert.- Què fareu?
Ls.- Sumar
Albert.- Qui ho sap fer amb el cap?
R.- 52
Albert.- Com ho has fet?
R.- 40+10+2
Albert.- Algú ho ha fet d’una altra manera?
Ls.- M’he imaginat el 40 i el 12 a baix i ho he sumat
Albert.- I ara ens queda aquest 32
Nens.-84

Albert.- Hi ha una altra cosa que no entenc: aquest número 6,14 cèntims. Tu el saps llegir?
C.- Que gasten 6 pessetes i 14 cèntims.
Albert.- Com ho saps?
C.- Perquè hi ha la coma
Albert.- Si volem que digui 6 pessetes al darrera hem de posar pessetes
Ls.- És igual que avui dia, diu 1 € i 30 cèntims i no posa cèntims, posa €
Albert.- Guanyen 140 rals i gasten 6,14 pessetes.. Podem saber si tenen prou? Què hem de fer per comparar?
(ningú aixeca la mà)
Albert.- Què hem fet abans?
Ls.- Hem canviat el 3 pel 0, ho hem buscat a la taula.
Albert.- M’estàs dient els passos que hem fet però jo pregunto per què.
P.- No podem comparar rals amb pessetes, hem de convertir les pessetes en rals.
Albert.- Com ho podem fer? On hem de mirar?
Nens.- A la pissarra
P.- Hem de passar els rals a pessetes
N.- No, les pessetes a rals perquè és l’época d’en Gaudí.
P.- Busquem 6 pessetes a la taula, quants rals són?
I.- He buscat 6 p i no hi és
Albert.- Què podem fer?
R.- 6 i mitja
I.- Deu ser més o menys 25
Pau.- He buscat 5 pessetes i són 20 rals.
6 són 25v Albert.-Si tenim a la taula que 5 p són 20 r, quantes pessetes falten?
N.- 1
Albert.- Quants rals són?
N.- 4
Albert .- Quant és 6 pessetes?
D.- 24 rals
P.- Jo ho hagués fet d’una altra manera.
Albert.- Digues
P.- ...No...no...
Albert.- Guanyen 140 rals i gasten 24... els en sobren molts... em sembla que heu calculat que menjaven massa poc...

Comencen a treballar per grups per calcular si en tenien prou o no la resta de famílies representades a la taula. La sessió d’avui ha mostrat que els continguts treballats resultaven força difícils per a la majoria dels alumnes i per tant no podíem pretendre que els assolissin d’una manera acabada. Mentre treballen es van reproduint alguns dels problemes, dificultats, idees i solucions que ja s’apunten a la conversa col•lectiva.

ALGUNES DE LES PROBLEMÀTIQUES QUE ES VA GENERAR QUAN ELS NENS I NENES ESTAVEN TREBALLANT

El sentit de la nostra mirada:
La reflexió que ve a continuació, centrada en l’explicitació de les diferents dificultats observades en els nens i nenes quan estaven realitzant aquesta tasca, no és la d’un judici sobre les coses que saben i les que no saben. La nostra observació és interessada, però la nostra mirada avaluativa va dirigida principalment a entendre els nens i nenes: entendre en primer lloc allò que fan, i també perquè ho fan. Imaginar el que podrien fer i què caldria per tal que ho fessin. Però especialment per a nosaltres representa la necessitat d’ imaginar el que podríem fer per ajudar-los a avançar. Des d’aquest punt de vista, l’avaluació es dirigeix en primer lloc cap a la nostra tasca, per tal de permetre l’obertura de nous camins en el seu aprenentatge. Però per a això, en primer lloc els hem d’entendre.

1. Problemàtiques respecte del sistema de monedes

- Calia diferenciar el valor cardinal del nombre del valor de la quantitat expressada per la relació entre aquell nombre i la unitat monetària. Alguns nens es fixaven només en els números per a realitzar les comparacions. Sovint els costava veure la importància de les unitats monetàries a l’hora de valorar les quantitats expressades.

- Calia prendre consciència que per comparar els diferents valors havien de transformar-los a la mateixa unitat. Això implicaria valorar quina de les transformacions és la més adequada. Els nens i nenes transformen cap als rals, en part perquè els sous estan tots en rals i potser en part perquè durant la transformació efectuada conjuntament en primer lloc decidim passar-ho a rals.

- Com es podria crear una discussió sobre això?

2. Problemàtiques relacionades amb la utilització de la Taula per calcular.

- Com llegir una taula de conversió d’unitats, complexa com la que vam donar, entre tres unitats. Per ex: de vegades es perdien de vista els valors de la unitat de partida i només utilitzaven com a element de decisió “buscar el nombre de partida” sigui a la columna que sigui. Possiblement respongui a les dificultats d’utilitzar la reversibilitat, tal i com ja es va plantejar anteriorment.

- La capacitat d’utilitzar-la com a eina per calcular. Per a això calia fer ús de l’estructura de la taula com a forma de mostrar i organitzar les equivalències cosa que representava algunes dificultats interessants:
Per exemple, si la quantitat que buscaven no hi era, calia descomposar-la en parts que sí que hi fossin representades, després buscar el valor de cada part i calcular el total . En aquest procés alguns nens es perdien i fins i tot podien cercar la quantitat a una altra columna.

- La capacitat per establir relacions adequades (diferència, proporció...) entre quantitats diferents expressades en la mateixa unitat (per ex. cèntims) per tal d’establir composicions numèriques que els serveixin per calcular, sense perdre de vista el seu valor. En alguns moments vam detectar dificultats en la comprensió de la composició additiva del sistema de numeració (veure el punt 3 a continuació).

- La capacitat per establir relacions d’equivalència entre les diferents unitats tenint clar que el valor de cada una de les quantitats composades (en cèntims ) té el seu corresponent en una altra (o altres, en aquesta taula) unitat: per ex. rals o ptes.

- La consciència que, de la mateixa manera que es pot fer la composició dins de la unitat de partida (per ex. composició (sumes...) entre dues quantitats expressades en cèntims per fer la quantitat en cèntims que es vol canviar ), s’haurà de fer la composició en les unitats d’equivalència d’arribada (rals o ptes). Vegeu la conversa.

3. Problemàtiques relacionades amb el sistema de numeració.

Aquest treball ens ha permès també detectar alguns problemes relacionats amb el sistema de numeració, i que veurem com s’hauran d’anar abordant:

- Cal tenir clar el diferent valor de les xifres. Ha de ser així per poder composar i descomposar quantitats noves. (Ex. de 1.300= mil + 300). Determinats nens no tenen clara la composició additiva, cosa que es manifestarà en el càlcul quan no tenen una consciència clara que la suma inclou tots els sumands. (vegeu sessió anterior)
- Hi ha nombres que no coneixen o no saben dir, i això pot expressar també dificultats en valorar quin és més o menys...
- Dificultats per vincular el valor dels nombres no només al cardinal sinó també a la unitat que representa aquest cardinal (1 milió >1000)

4. Problemàtiques relacionades amb el càlcul

- Hem vist en alguns nens dificultats derivades d’un poca comprensió del sistema de numeració: per exemple de quines maneres diferents podem fer el nombre 80. O com podem construir sèries amb unitats compostes.

- Valorem certa dependència del càlcul realitzat amb els algoritmes i dificultat de valorar el paper del càlcul amb el cap. El càlcul “mental” per a alguns alumnes és imaginar-se l’operació i fer-la igual que al paper!

- Força nens tenen dificultat en desvincular-se de la pretensió de l’exactitud en el càlcul, cosa que els podria ajudar a fer aproximacions, enquadraments (entre tal i qual) estimacions, a desestimar quantitats massa mínimes que destorben el càlcul, guanyant d’aquestes maneres en flexibilitat.

- En algunes respostes sembla haver-hi molta càrrega de prejudicis, d’expectatives sobre el que s’espera que digui.

- Possibilitats de treballar la numeració i el càlcul.
- Una llibreta-diari personal?---Jocs- Racons?---Treball sistemàtic a estonetes? Problema de l’horari
- La multiplicació – i els problemes que tenim pendents

Com a la resta de les sessions analitzades al document participen tres adults: la Marta (tutora, que gestiona la sessió), l’Albert ( com a assessor que observa i intervé quan s’escau),i la Bea (mestra suport, que observa i registra la situació). Recordem els tres alumnes: A., An ,i X amb greus dificultats per l’aprenentatge de les matemàtiques.

Durant aquesta sessió es realitzen dos treballs:

1. El primer es refereix a la posada en comú d’un text elaborat per cada nen on s’explica el que per a ell ha estat “La història dels Rals”

2. Posteriorment es treballa sobre la pregunta, pendent, de la P.: Si un € té 100 c i una PTA també, són iguals? i ho aprofitem per fer servir una taula d’equivalències més propera als nens, un traductor de ptes i euros.

1. Es proposa la lectura col•lectiva dels textos realitzats individualment la sessió anterior. Com que previsiblement no es podran llegir tots, els alumnes opinen sobre quina serà la manera millor de procedir (ordre alfabètic, sorteig...)

Tutora..- Ahir vàreu escriure tot el que recordàveu del que havíem fet fins ara sobre el que la gent guanyava a l’època d’en Gaudí i si era suficient per viure. Alguns nens no van acabar i s’ho van endur a casa. (diferents nens lliuren el seu full. L’A. no es mou)
An, el teu no el tinc, busca’l a la carpeta (l’A., sense esma, obre la carpeta i treu un full amb cinc o sis ratlles escrites i li dóna )... Molt bé
A.- Ahir no vaig sopar perquè la meva mare...
T.- Em sembla que no tindrem temps de llegir-los tots...
A.- Un dia que tinguem temps els podrem llegir.
O.- Podem començar per ordre d’abecedari.
Ll.- Qui el vulgui llegir que aixequi el braç i sorteges.
Tutora.- Són semblants o diferents?
N.- Semblants
I.- A lo millor són semblants
R.- El llegirem cadascú?
Ll.- Tots vàrem fer grups i la informació pot ser més o menys igual però no la mateixa..
Tutora.- Pot ser que hi hagi coses diferents, que uns expliquin una cosa i els altres en recordin d’un altra.
P.- Uns llegeixen i si està repetit no cal repetir.
A.- (explica un sistema de sorteig)
Tutora.- Potser hi ha coses diferents. La I., per exemple, ha escrit una cosa que poca gent ha explicat.
R.- El meu és com una història i podia haver escrit més coses que ara me’n recordo i ahir no i a més estava cansat.

Es realitza la lectura. L’acord ha estat escoltar amb molta atenció i aixecar la mà si tenim informació nova. També si hi ha alguna cosa amb la que no hi estiguem d’acord. Quan ja se n’han llegit bastants es reparteix la resta perquè els autors subratllin només els paràgrafs no dits per llegir només aquests

Tutora.- Agafo un full sense mirar... J! (el J. tot ell es transforma, es revifa). Mentre escoltem al J. pensem si tenim coses diferents, alguna cosa que el J. no hagi dit.
R.- Cadascú ha d’entendre la seva lletra.
Tutora.- In, què farem ara?
In.- Si hi ha “algo” que no és igual... (parla molt fluix)
Tutora.- Més fort
In.- (continua explicant una mica més fort)
Tutora.- (torna a repetir el que ha dit l’In)
J.- (Llegeix amb dificultat)
P.- No ha escrit una cosa...
Tutora.- Vine , P.
N.- Han de cridar més
P.- (Llegeix)
R.- Jo tinc una altra cosa.(Llegeix)
M.- Jo tinc més coses (Llegeix)
Tutora.- Ara ja n’hem llegit uns quants. Pensem si entre tots aquests ha quedat alguna cosa important sense explicar.
S.- (Llegeix)
Tutora.- Sí que tenies coses noves, sort que ho has vist!
O.- S’ ha equivocat: 5 cèntims no són 5 pessetes.
Tutora.- Hem d’escoltar si el que diuen és veritat o s’han equivocat.
A.- Hi ha una cosa que no ha dit
R.-. El J. està dibuixant.
Tutora.- No sé si pot escoltar a la vegada que dibuixa.
A.- (Llegeix a poc a poc amb una mica d’ajut de la Marta)
An.- L’A. s’ha equivocat, ha posat monedes...
Tutora.- L’A. ha explicat una cosa que ningú havia dit: que els nens treballaven.
Al.- Ha posat 4 rals, en comptes de 20 rals.
Tutora.- Veig que tots heu explicat coses interessants,i alguns diferents.
Ll.- (Llegeix)
An.- (mira tots els textos que la Marta ha deixat damunt la seva taula)
J.- T’has equivocat perquè has dit P. i A. i havien estat el P. i l’I. els que van trobar la informació.
Tutora.- Ho tens ben escrit però t’has equivocat al llegir..
S.- (Llegeix)
R.- Quants més en llegirem?
Tutora.- Ara ja hem d’afinar molt. Penseu si de veritat hi ha alguna cosa que no s’hagi dit perquè potser s’ha dit amb altres paraules.
An.- Jo tinc una cosa.
N.- Abans s’ha equivocat, un ral no és mitja pesseta.
An.- ( La Marta li ha d’anar llegint perquè ell ho repeteixi)
Tutora.- L’Adrià té un problema i és que és la meva lletra i costa una mica d’entendre.
Has dit que ho buscaves amb la calculadora i això encara no havia sortit.
E.- (Llegeix)
R.- Jo he vist un problema...però no era un problema... deia rals amb una erre
Tutora.- La M. C.
Grup.- No! Ha escrit molt!
Tutora.- Voleu dir que ja ho dirà tot? Ha treballat molt i ara la feinada és nostra d’escoltar.
(Ve la mare d’un nen a la porta)
Ara repartiré els textos que encara no hem llegit perquè els repasseu i marqueu el que encara no s’hagi dit.
X.- (Llegeix a estrebades)
X.- (Llegeix)
Tutora.- Ningú havia escrit fàbrica tèxtil.
(Llegeixen el que tenen subratllat: I. ,Ls. ,P., C. , G. , O. , Al., In.

Tutora.- Entre tots ho hem anat recordant tot!
Observem com es generen, a partir de les lectures, la circulació d’informació i el sentiment de comunitat d’aprenentatge: Entre tots recordem totes les coses importants. Sorprèn l’atenció que posen per si hi ha errors i per si ells poden aportar informació nova.

També és rellevant com participen tots i la tutora pot afavorir la intervenció dels nens amb més dificultats: suport a l’organització (lliurament de fulls), a l’atenció (pregunta què ha dit que farien), a l’escriptura i lectura individuals, a comportaments d’ansietat (permet que en certs casos es pugui dibuixar)

Aquest quadre és un resum de la quantitat de vegades en què un determinat tema surt en el conjunt de les narracions dels nens i nenes de la classe. Com veiem, les tasques es refereixen a “La història dels rals”, no al conjunt del projecte. No obstant, per a aquests nens, és una evidència que aquesta història forma part del projecte: es mostra tant la decisió sobre el projecte com sobre la vida de les persones en l’època de Gaudí. I no només sobre la temàtica sinó sobre els processos generals, sobre les accions que necessitem dur a terme per fer el projecte, com el “buscar informació”, “posar idees en comú... explicar als altres...”,”treure conclusions, valorar...”. Els aspectes relacionats amb el càlcul hi tenen una forta presència, però ni de lluny són els únics. Es poden rastrejar en els seus textos, i també en el quadre, els diferents vincles que per a ells han estat importants: les persones, ells com a grup, el seu projecte, les necessitats de trobar respostes, les accions que han dut a terme, siguin o no matemàtiques, ...

2- Es passa a debatre sobre la pregunta plantejada per una alumna: Si 1 € té 100 c i una pta també té 100 c, són iguals?. Aquesta pregunta la va plantejar ja a la primera sessió i se’ls va demanar que la parlessin a casa per veure quina resposta hi podríem trobar. Durant la setmana se’ls ha recordat

Tutora.- La P. va fer una pregunta i la vàrem guardar per contestar-la més endavant. “Si una pesseta té 100 cèntims i un € té 100 cèntims, és el mateix?” Alguns van preguntar-ho als pares. Ara el J. recollirà els textos i jo repartiré les respostes que vàreu portar perquè ja fa molts dies i així ho refresqueu.
G.- No és el mateix, el cèntim de pesseta té menys valor que el cèntim d’euro.
Tutora.- Què vols dir?
R.- Ara tenen més valor els euros perquè ara s’utilitzen els euros i abans les pessetes perquè s’utilitzaven.
Al.- 1 € és diferent d’una pta perquè un traductor diu 1 € = 163 ptes
Grup.- 166!
Ls.- El meu pare m’ho va dictar . No és el mateix, igual com els rals i les pessetes.
(llegeix) 1 € són 100 cèntims? Sí
1 pta són 100 cèntims? No
Tinc una xuleta ( ho còpia a la pissarra) 1€ = 166,386 p.
Sé quantes pessetes necessito per fer 1 € i quant euros per fer 1 pta.
E.- En 1 € hi ha 166 cèntims, en 1 pta hi ha 100 cèntims.
C.- 166 ja són pessetes i no cèntims
P.- (dibuixa a la pissarra dues tires llargues i fa petites parts). Si això és 1 € (tota la tira), això (part) és un cèntim. I amb una pesseta també.
Com que 1 € és 166 , és un cèntim d’euro.
So.- No és el mateix : 1 € = 166,386 ptes (es refereix a l’equivalència anterior: 166)
In.- És el mateix
D.- El meu pare em va apuntar:
1 dòlar té 100 cèntims de dòlar
1 € té 100 cèntims d’euro
1 pta té 1oo cèntims de pta
Albert.- Aquest nen diu coses que no ha dit ningú. Llegeix ben fort que ho escriuré a la pissarra
D.- És que el meu pare és banquer.
Albert.- (Ho escriu), i diu: “Marta, aixeca la mà”. (les tres Martes aixequen la mà). N’hi ha prou en dir Marta ? ... No!, cal dir quina Marta !!. ...Si jo dic 10 cèntims sabeu el valor?
C.- Has dit 10 cèntims però no de què.
Albert.- He de dir si tinc 10 cèntims de dolar o d’euro
Grup.- O de pta, o de la Xina, o d’Alemanya
Albert.- és important que recordeu (emmarca el que havia escrit a la pissarra) perquè els cèntims de pta no són el mateix que els d’euro.

Es pot veure, entre altres qüestions, els vincles afectius que donen importància a la informació que porten de casa seva : “el meu pare m’ha ensenyat a fer una xuleta”,” el meu pare és banquer”, ”la meva mare m’ho va explicar amb aquest dibuix i ja ho vaig entendre” .

A continuació es proposa un joc d’afirmacions sobre les equivalències €, pta i c per valorar si són o no correctes.

Albert.- Jo diré coses i vosaltres em direu sí o no
“1 € té 166 cèntims”
E.- No
Albert .-“1 pta té 100 cèntims”
N.-Sí però has de dir “de pta”
Albert.-“1 € val 100 ptes” Què dius Xènia?
Xènia.- No
Albert.-“166 ptes són 1 €”
Grup.- Sí
Albert.- “166,386 ptes són 1 €”
J .- No
Albert.- Tothom està d’acord?
Grup.-Sí

Albert.- Aquí ens passa una cosa: 166 ptes= 1€ ; 166,386 ptes= 1 €
Ell diu que no pot ser, però és que aquest trosset (subratlla els decimals 386) com que és molt petit no el contem..

- Observem les dificultats de comprensió de molts nens sobre les relacions part /tot (centims d’euro, de pesseta i de dòlar), de reversibilitat (sé els € que necessito per a fer 1 pta)

PRESENTACIÓ DEL “TRADUCTOR” DE PTES/€. Desperta una gran motivació pel seu ús i funcionament. Amb ell anem realitzant diferents conversions

Albert.: Ara us donaré una cosa a veure si us sona i podreu jugar amb la Marta algun dia.
(repartim un full on hem ampliat una targeta de reconversió euros/ pessetes)
Que aixequin la mà els que no saben què és
Grup.- (aixequen mans)
Albert.- Qui els vol ajudar?
Jo. i L.- Un “quién és quién” de números.
Albert.- (mostra la targeta petita que hem ampliat)
Al.- Un traductor d’euros a pessetes.
Al.- A veure com funciona. Jo veig rodones i rectangles. Què són les rodones?
D.- Són les monedes
Albert.- I els rectangles?
Xe.- Els bitllets
Albert.- Què vol dir l’estrella?
S.- Perquè fa 1 €
Albert.- Vosaltres teníeu un traductor de pessetes, rals i cèntims, i ara teniu aquest. Qui sap com funciona? Anem a jugar. 166 ptes ,on veig quants € són?
Grup.- 1 €
Albert.- Ara penseu preguntes.
A.- 2 €?
Albert.- 2 €, on trobem quantes pessetes són.
R.- 332
A.- 3 €?
M.- 4 €?
Jo.- 666
Albert.- Què?
Jo.- pessetes
O.- 13 €?
L.- 2.163 ptes
Albert.- Algú que pregunti pessetes i ho direm en €
E.- 49.916 ptes
An .- (amb ajut) 300 €

L’activitat continua i acaba amb la mateixa dinàmica. Veiem que amb aquesta activitat s’han establert nous vincles i relacions, tant amb noves persones (especialment les famílies) com entre continguts matemàtics (els sistemes de monedes, la eina simbòlica que representa la taula com a “traductor”,...