LUGARES GEOMÉTRICOS
ASOCIADOS A TRAYECTORIAS.
A lo largo de este tema vamos a trabajar con SGD(sistemas de
geometría dinámica), Entendiendo por sistemas de geometría dinámica
un conjunto de recursos que permitan trabajar propiedades geométricas a través
del movimiento. El software SGD que utilizaremos será GEOGEBRA, y el recurso no
informático será el Espirógrafo. Otros sistemas que podríamos
utilizar serían pantógrafos, mecanos, geoplanos, etc.
Inicialmente utilizaremos el Espirógrafo y más
tarde Geogebra.
El contenido que queremos desarrollar es el de LUGAR GEOMÉTRICO
en el plano. Puesto que todo lugar geométrico lleva asociado un
gráfico, que puede ser un punto, una curva (recta como caso particular) cerrada
o no (poligonal como caso particular) o una superficie, queremos que el recurso utilizado la dibuje, para
que el alumno pueda comprobar cuál es el gráfico asociado al lugar.
El concepto de lugar geométrico,
conjunto de puntos que cumplen una determinada condición, se estudiará a través
de trayectorias,
por lo que las condiciones
que cumple el lugar van a ser las asociadas a ese movimiento: giro
(centro, ángulo), traslación (vector), equidistancia (a puntos, rectas),
rodadura y resbalamiento (composición de movimientos). Recordamos que en física
se define Trayectoria, como el lugar geométrico de las sucesivas posiciones que un móvil
va ocupando en el espacio, la línea descrita por el móvil en su movimiento. Los problemas contextualizados se basarán también en esta idea, por
ejemplo problemas de rodadura o de persecuciones.
Las situaciones
didácticas se pueden presentar desde dos aspectos:
a) Conocer las condiciones del movimiento y averiguar
cuál será la trayectoria.
b) Conocer el gráfico de la trayectoria y averiguar cómo
se ha formado.
Entendemos que lo primero es más fácil que lo
segundo, pues éste requiere una experiencia previa en la formación de lugares.
EL ESPIRÓGRAFO
Inventado
por Denys Fisher en el año 1965, el
juego consiste en una serie de piezas de plástico, inicialmente círculos y
reglas con bordes dentados, que al engranarse unos con otros permiten que éstas
giren sin deslizarse. Dentro de cada
círculo hay varios agujeros colocados a distintas distancias del centro de la
circunferencia. Al introducir el lápiz por ellos se generan dibujos que
dependen del tamaño del círculo móvil (su número de dientes), del agujero
seleccionado, de la pieza elegida como base del giro (regla o circunferencia y
su número de dientes), y de la posición del móvil respecto a la base.
Podemos ver
modelos de espirógrafo en la web http://www.samstoybox.com/toys/Spirograph.html
y el anuncio publicitario hecho para la televisión en el año 1973 o muestras de
su uso en You Tube.[1]
Actualmente
no es un juego fácil de conseguir, de hecho las versiones antiguas se venden en
las subastas de internet, pero sí podemos comprar algunas variaciones de éste
que no son tan completas como la inicial.
En España
puede encontrarse en la cadena de tiendas Imaginarium[2],
el juego se llama "1000 IMAGE", pertenece a la categoría de arte y
manualidades y se propone para edades de
EL
juego 1000 IMAGE es bastante limitado en cuanto a piezas, comparado con el
inventado por Fisher.
Contiene
siete círculos dentados, con el número de dientes indicado en cada uno de ellos
y son: 17, 22, 22, 27 29, 30, 33; tres plantillas con forma rectangular en cuyo
interior, además de otras figuras para dibujar contienen, una de ellas un
circulo de 48 dientes, la segunda una elipse de 64 y la tercera un corazón con
78 dientes; y finalmente, otra plantilla con distintas formas para dibujar pero
sin trazos dentados. EL juego carece de regla dentada.
Posibilidades
gráficas:
Como mencionamos anteriormente los
dibujos dependen de la selección de varios elementos:
- La pieza que gira, que llamaremos ruleta.
- La pieza fija, que denominaremos base.
- La posición de la primera respecto
de la segunda (interior o exterior)
- La relación entre ambas (número de
dientes o el equivalente tamaño del radio)
- El punto dónde se coloca el lápiz
(más cerca o más lejos del centro del círculo).
¿Qué tipos
de curvas podemos generar?
Respondemos
a la pregunta suponiendo que tenemos un juego que incluye como bases reglas y
círculos. Hablaremos indistintamente de círculos y circunferencias ya que ambos
aparecen con las mismas funciones en juegos reales y virtuales.
Para ponernos en situación, una
curva ruleta es la que genera un punto de una curva que rueda sobre otra
(incluimos la recta como caso particular de curva). Si la primera curva es una
circunferencia, estas se llaman cicloidales, son las que podemos dibujar con el
espirógrafo, y por eso también se les conoce como curvas espirógraficas (en
inglés, Spirograph Curves).
Veamos una clasificación de éstas:
|
Curvas CICLOIDALES |
||||
|
Ruleta (generatriz) |
Base (directriz) |
Nombre |
Posición de la ruleta |
Casos particulares con nombre
propio |
|
Circunferencia |
Recta |
Cicloide o trocoide |
------------ |
---------------------------------------- |
|
Circunferencia |
Circunferencia |
Hipotrocoide o hipocicloide |
Interior |
Deltoide, astroide, flores … |
|
circunferencia |
circunferencia |
Epitrocoide o epicicloide |
exterior |
Caracol, nefroide … |
En lo que sigue, hablaremos de
trocoides refiriéndonos a los tres casos.
Las curvas cicloides, tienen también
una clasificación según la posición en la rueda del punto que marca la
trayectoria:
Naturales, si el punto que describe
la trayectoria de la curva está situado en el perimetro de la rueda; alargadas,
si el punto que describe la trayectoria de la curva está situado en su
exterior, y acortadas, si el punto está situado en el interior.
Se suele reservar el nombre de
Hipocicloide y epicicloide para las curvas en las que el punto de la
trayectoria está situado en la forma natural, es decir, exactamente en la
circunferencia, y epitrocoides o hipotrocoides para las curvas acortadas o
alargadas; sin embargo no existe consistencia en el uso de estos términos, en
muchas ocasiones trocoide y cicloide se utilizan como sinónimos y sólo se
distinguen los prefijos Epi e Hipo como referencia a la posición de la ruleta
en el exterior o en el interior.[3]
La curva es
el resultado de la composición de dos movimientos,
por una parte la traslación de la circunferencia ruleta, y por otro por su rotación,
y como hemos visto en
el juego solo es posible la posición interior del lápiz (trocoides acortadas).
SIMULADORES Y PROGRAMAS
Buscando en la red Spirograph o
espirógrafo, encontramos applets y flash que simulan su funcionamiento. EL
requisito mínimo para poder trabajar con él de manera virtual es la
configuración del radio de las circunferencias, la distancia del punto que
marca la trayectoria, y la posición interior o exterior de la ruleta. La web de
educación plástica
http://www.educacionplastica.net/CurCic2.htm
ofrece un simulador de epicicloides e hipocicloides con el que podemos
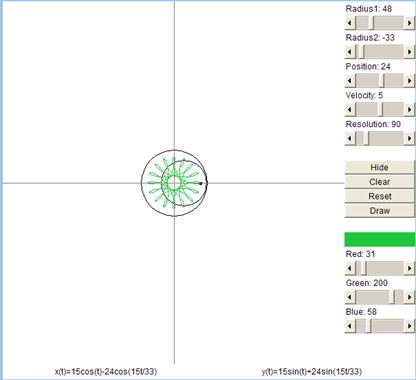
comprobar distintas conjeturas sobre las posibilidades de nuestro juego. En la
imagen vemos el resultado para los valores de radio de la base de 48 (equivale
a 48 dientes), y la ruleta de 33. El valor negativo indica la posición interior
de ésta. Se ha asignado un valor de 24 para la posición del lápiz.
Además, en la parte inferior del
applet podemos ver la ecuación de la curva dibujada en coordenadas paramétricas.
El mismo applet se puede descargar para trabajar offline en la web http://www.dadazi.net/new/batty/spiro/spiro.html
Disponemos en la misma web de
aplicaciones flash que dibujan separádamente, la cicloide, la hipocicloide y la
epicicloide, configurables en color, trazado, y que permiten ocultar la base y
la ruleta, para poder imprimir las curvas resultantes, de gran belleza.
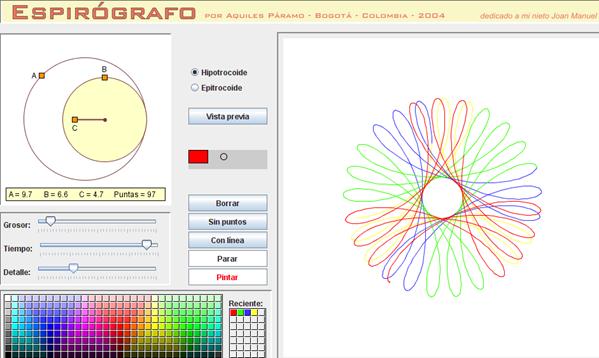
Probablemente la web más completa
del espirógrafo en nuestro idioma sea la del profesor Aquiles Páramo Fonseca,
de Colombia[4].
Uno de los temas que incluye dentro del módulo de cálculo integral es el
titulado "La gran belleza de las trocoides". En él nos introduce en
el munde de estas curvas, nos explica propiedades y ecuaciones, y nos aporta multitud
de imágenes elaboradas con el programa espirógrafo desarrollado por el autor.
La única dificultad que presenta a la hora de configurar es que la selección
del radio de la circunferencia se hace a través del arrastre del ratón y no
siempre conseguimos de manera exacta el número deseado. A pesar de esto, merece
la pena probar suerte con este programa, porque la posibilidad de modificar los
datos iniciales de la curva en el momento de su realización da lugar a multitud
de resultados, cada cual más bello. Visitar la galería de espirogramas de esta
web es un paseo que recomiendo a cualquier amante de las matemáticas y del
arte.
CONEXIONES CURRICULARES:
El
espirógrafo puede ser el elemento motivador para el inicio del estudio de la
geometría dinámica. Así, igual que el director de una película cuida hasta el
más mínimo detalle en los minutos iniciales para captar la atención del
espectador y conseguir que no se mueva de su asiento, nosotros podemos captar
la atención de nuestros alumnos a través de la intriga que las piezas del juego
y sus distintos engranajes pueden generar en su mente. Las curvas nacen del
movimiento, a través de nuestras manos, sin esfuerzo ni conocimientos previos,
y cada una de ellas será propia, personal, diferente.
En un primer momento solo nos interesa que
dibujen,
que exploren, que busquen distintas formas de combinar las ruletas. Después
querremos que indaguen, que piensen por qué surgen hojas alargadas o acortadas,
de qué depende el número de hojas obtenidas, si el dibujo es finito (la curva
se cierra) o infinito (la curva no se cierra), cómo influyen los números que
aparecen marcados en el juego (número de dientes y número del agujero). Más tarde sentirán la necesidad de
obtener otras curvas más complejas, con números que no están en las piezas del
juego, entonces será el momento de utilizar el ordenador, los simuladores
virtuales del espirógrafo.
Finalmente, el modelo matemático. Hemos generado
curvas cíclicas, lugares geométricos. Algunos sencillos de obtener a partir de
condiciones geométricas y otros a partir de ecuaciones paramétricas o polares.
Para los primeros, Geogebra, Cabri, CarMetal, o cualquier otro software de
geometría dinámica; para los segundos, software gráfico que permita los tres
tipos de coordenadas, cartesianas, polares y paramétricas; Wiris, Winplot,
Graphmatica, o GrafEq, entre otros, y las calculadoras gráficas, más manejables
y económicas, con las que podemos hacer una investigación sobre la influencia
de los parámetros de la expresión de la curva en su forma a partir de 4º de
ESO.
ACTIVIDADES PARA EL PRIMER CICLO DE ESO.
LUGARES GEOMÉTRICOS: CURVAS CÍCLICAS
BLOQUE I: ACTIVIDADES INICIALES
Contenido: Curva,
como lugar geométrico descrito por un punto que se mueve siguiendo una ley
específica. Curvas abiertas y cerradas. Curvas cíclicas: Curvas históricas.
Recurso: el espirógrafo
Organización de la clase:
Los alumnos se colocan en grupos de 4. Cada grupo dispone de un juego. Uno de
ellos anota los comentarios de sus compañeros.
Objetivos:
·
Buscar un modelo matemático en una situación de
juego.
·
Favorecer la competencia comunicativa e
investigadora.
·
Valorar las matemáticas como herramienta para el
estudio de otras materias (física y plástica) y del mundo que nos rodea, y como
instrumento para el diseño y construcción de obras artísticas.
Para ello tendrán que utilizar distintas estrategias matemáticas:
Establecer un plan de trabajo individual y para el
grupo, elaborar conjeturas, ensayarlas y experimentarlas, observar e interpretar
los datos obtenidos, deducir relaciones, expresarlas verbalmente y por escrito,
utilizar el vocabulario y la notación adecuada, contrastar y evaluar los
resultados, buscar una situación de aula o real a la que se puedan aplicar.
Las actividades están pensadas para realizar cada
una de ellas en una sesión de 50 minutos.
ACTIVIDAD 1: El juego del espirógrafo
Esta actividad es fundamentalmente
de motivación. Al ser la primera vez que los alumnos utilizan el juego del
espirógrafo es necesario dejar un tiempo para que disfruten de él. Así mismo
tenemos que "negociar" la organización de la clase, formación de los
grupos, papel que desempeñará cada alumno, tiempos que dedicaremos al trabajo
en grupo y a la puesta en común.
Suponemos que los alumnos utilizarán
el juego en la posición de giro interior de la ruleta (hipotrocoides), si esto
no es así hay que abrir más líneas de investigación porque las posibilidades
aumentan y requerirá más tiempo.
Finalmente hay que adquirir
vocabulario específico. Algunas palabras nuevas requerirán definiciones que
puede dar el alumno, buscarlas o directamente explicarlas el profesor.
VOCABULARIO: Ruleta,
base, traza, trayectoria, generatriz, directriz.
Objetivos:
Conocimiento del juego y su funcionamiento. Investigación sobre formas posibles
de colocar sus piezas y resultados gráficos de éstas.
Se pretende que el alumno además de
disfrutar con el juego haga una clasificación de las figuras obtenidas en base
a alguna referencia que él debe buscar, por ejemplo, el tamaño, colocando las ruletas
de menor a mayor y asociando éstas a las curvas obtenidas. También debe
explicar qué dibujos le gustan más y por qué (tal vez simetrías, formas
redondeadas, similitud con objetos naturales, flores …)
Al alumno se le informa de que la
pieza que gira recibirá el nombre de ruleta o generatriz, y a la que está
inmóvil se le llamará base o directriz. El punto donde colocamos el lápiz se
llamará punto P, como incial del la palabra "Pinta"
Desarrollo
de la actividad:
·
Para
cada una de las ruletas haz varios gráficos. Estudia en cada uno de ellos
similitudes y diferencias, clasificalas y anótalas.
· Realiza un
diseño personal con el juego y explica a los compañeros cómo se ha elaborado y
cuáles son sus características (número de hojas, simetrías, colores, etc)
· Expón a la
clase las conclusiones obtenidas.
ACTIVIDAD 2: RELACIONES NUMÉRICAS
La actividad está enfocada hacia la
búsqueda de relaciones numéricas concretas, y por lo tanto predicción de la
forma del dibujo antes de realizarlo a partir de éstas relaciones.
VOCABULARIO/contenidos: fracción
irreducible, divisores, múltiplos, ciclo.
Objetivo:
Descubrir
la relación que existe entre el número de dientes de la ruleta, de la base y el
dibujo obtenido.
Se
trabajan 2 propiedades[5]:
- El número
de hojas
- El número
de ciclos (vueltas que da la ruleta sobre la base) para que el dibujo se
cierre
Desarrollo
de la actividad:
· Busca una
relación entre el número de hojas que tiene un dibujo y el número de dientes de
la ruleta y la base elegida. Busca
ruletas que lleven al mismo número de hojas.
· Haz una
predicción sobre el número de hojas que tendrá un diseño en función de la
ruleta y la base elegida y compruébalo.
· Busca
relaciones entre el número de vueltas que da la ruleta sobre la base (ciclos) y
el número de dientes de éstas.
· Analiza si
todos los dibujos se cierran o se puede dar algún caso en el que esto no ocurra
· Investiga
cómo afecta la colocación del lápiz en cada ruleta al resultado del dibujo.
· Haz varios
dibujos e intercámbialos con los compañeros de otros grupos para qué éstos
averiguen cómo fueron hechos.
ACTIVIDAD 3: INVESTIGANDO CURVAS CÍCLICAS 1.
Objetivo: Investigar
los nombres de las curvas obtenidas y comprobar las relaciones de la actividad
2. Obtener nuevos casos no configurables con el juego.
VOCABULARIO/contenidos: Curvas
cíclicas/ruleta, epi/hipocicloides (o trocoides), lugar geométrico. Para poder
utilizar el simulador virtual los alumnos deben conocer la suma y diferencia de
números negativos.
Recursos: : Simuladores virtuales del juego. Descargaremos un simulador
virtual de la web http://www.dadazi.net/new/batty/spiro/spiro.html.
También podemos trabajar directamente con los applets en las webs http://www.educacionplastica.net/CurCic2.htm
o bien http://temasmatematicos.uniandes.edu.co/Trocoides/paginas/espirografo.htm.
En esta última disponemos de muchos ejemplos de curvas
hechas con el simulador.
Necesitaremos
un ordenador para cada pareja de alumnos. También podemos plantear la actividad
con un portátil para cada grupo de 4. En este caso uno trabajaría en el
ordenador, otro anotaría conclusiones, y los otros dos buscarían el equivalente
al dibujo del ordenador con el espirógrafo real
Desarrollo
de la actividad:
1. Entra en la
web de educación plástica. Al final de la página hay un apartado sobre curvas
cíclicas. Averigua cuál es el nombre de las curvas que hemos estado dibujando.
2. Dibuja
utilizando el flash de la aplicación más curvas cíclicas combinando colores y
formas
3.
Hay
una curva cíclica llamada cicloide,
¿puedes hacerla con el espirógrafo?
4. Comprueba
con el simulador del espirógrafo las fórmulas obtenidas en la actividad 2.
5. ¿Qué valores
le tienes que dar a la posición del lápiz para que la curva pase por el centro
de la circunferencia base?
ACTIVIDAD 4: HISTORIA DE LAS CURVAS CÍCLICAS.
Objetivos:
· Situar en la
historia las curvas cíclicas (dado el nivel para el que se plantean estas
actividades no podemos profundizar en su implicación histórica, pero sí
plantear una iniciación que se puede continuar en cursos posteriores, sobre
todo en bachillerato).
· Conocer sus
implicaciónes en otras asignaturas, en este caso, física y plástica.
Recursos: Artículo de Antonio
Pérez Curvas con historia: de las cónicas a las ecuaciones de las flores.
Desarrollo
de la actividad:
Nos situamos en la antigua Grecia, siglo
VI A. C., Los griegos introducen los problemas de construcción. Én estos
problemas todas las figuras deben ser construídas utilizando solo una regla y
un compás. Parecido a lo que ahora hacemos en las clases de dibujo. Pero tres
de los problemas que plantearon no eran capaces de construírlos con esos
instrumentos, y se convirtieron en los tres problemas clásicos de la geometría:
§ La cuadratura del círculo: construír
un cuadrado con la misma área que un círculo dado.
§ La trisección del ángulo: Dividir un ángulo
en tres partes iguales
§ La duplicación del cubo: Construir
un cubo con el doble de volumen que un cubo dado
Se tardaron siglos en demostrar que
esos problemas no se pueden resolver con regla y compás, hubo que esperar a la
aparición de nuevas ramas de la geometría que estudiarás más adelante. Pero
intentando resolver estos problemas, y otros, como el movimiento de los
planetas se descubrieron nuevas curvas, las llamadas mecánicas, entre las que están nuestras curvas espirográficas.
1. Investiga si
las curvas cíclicas pueden ser construídas con regla y compás. Pregúntale al
profesor de dibujo. Pregúntale también por los tres problemas anteriores y
elabora un resumen con las conclusiones.
2. Lee las
páginas 5 y 6 del artículo de Antonio Pérez Curvas con historia: de las cónicas
a las ecuaciones de las flores, en ellas habla de Ptlomeo y su modelo del
universo. Explica qué relación guarda con las curvas cíclicas.
ACTIVIDAD 5: SITUACIONES REALES Y PROBLEMAS CON CURVAS CÍCLICAS
Objetivo: Trabajar situaciones reales
en las que aparezcan curvas cíclicas y relacionarlas con la arquitectura y el
arte.
Desarrollo de la actividad:
1.
En
la imagen puedes ver el rosetón de
la iglesia de Santo Tomé de Serantes, en
2.
Utiliza
el espirógrafo para resolver el siguiente problema:
Se toman dos monedas del mismo tamaño y, fijando una de ellas, se
gira una alrededor de la otra.
¿Cuántas vueltas da sobre sí misma?
Intenta averiguar una relación entre
el número de vueltas y los radios o el número de dientes de la ruleta y la
base.
3. 
Causticas: son curvas creadas por la
reflexión o refracción de la luz al incidir sobre un objeto.
Investiga qué sombra se obtiene en
el fondo de un vaso y fotografíala.
4. Logotipos: En la imagen puedes ver
distintos diseños de logotipos. Indica si alguno tiene que ver con los dibujos
del espirógrafo.
Haz un diseño de un logotipo para la
clase y explica cómo lo has realizado dando su construcción y propiedades
matemáticas. El más votado por todos será el que la represente.
5.
Diseños
artísticos:
En las imágenes puedes ver una lata de mejillones con un diseño de Sargadelos y
diseños de encajes de Camariñas. Investiga en tu casa si hay algún motivo que
se asemeje a los del espirógrafo. Fotografíalo y explica sobre la imagen sus
propiedades.
ACTTIVIDADES DE AMPLIACIÓN:
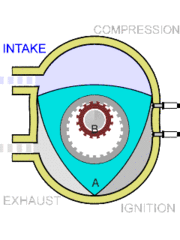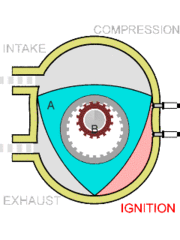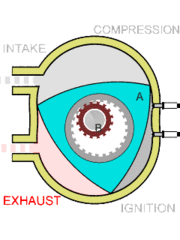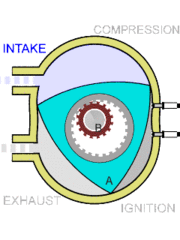
6. Motores: El motor Wankel fue inventado por
Wankel en 1924 y se basa en una hipocicloide. Puedes ver la imagen en
movimiento en
Observa en el video el
funcionamiento del motor y explica similitudes y diferencias con los
movimientos que se utilizan en el espirógrafo.
La figura exterior se llama triángulo de Reuleaux, investiga qué propiedades y usos tiene.
7.
Cicloide: En la
cubierta de la rueda de tu bici señala con tiza un punto que se vea bien de
lado. ¿Qué curva recorre ese punto cuando te mueves con la bici por la carretera?[6]
¿qué elementos del espirógrafo precisas para dibujarla? Investiga sobre sus
propiedades físicas.
8.
Perfil
geométrico de las olas: El perfil geométrico de las olas sigue una
trocoides. Entra en la web http://www.mailxmail.com/curso/vida/meteorologiageneral/capitulo16.htm y descubre cuándo son estables e inestables,
y en qué elementos matemáticos nos basamos describirlo.
9.
Las
espirales
son otro modelo de curvas importantes en la física, la naturaleza y el arte.
¿Podríamos hacer espirales con el espirógrafo? Razona la respuesta e indica qué
movimientos requiere la construcción de una espiral.