Problemes de la primera fase (2002)

PROBLEMA 1. Ordena les xifres del 0 al 9 de manera convenient, per tal que en llegir els nombres que resulten d'agrupar-les de dues en dues, et permeti obtenir el major nombre de punts, segons el següent escandall:

• Per cada Nombre Primer: 1 punt
• Per cada Nombre Quadrat: 2 punts
• Per cada Nombre Triangular: 3 punts

Per exemple, si ordenem 1, 5, 2, 3, 0, 4, 9, 7, 8 i 6, obtenim els nombres 15, 52, 23, 30, 4, 49, 97, 78 i 86

I la puntuació obtinguda és: 3 + 0 + 1 + 0 + 2 + 2 + 1 + 3 + 0 = 12

Recordes quins són els nombres quadrats?

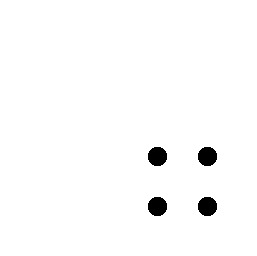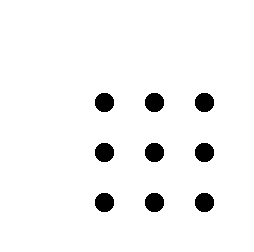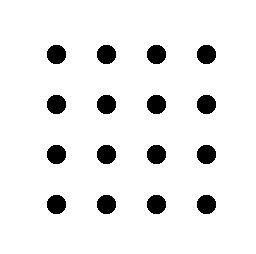1	4	9	16	...

I els nombres triangulars?

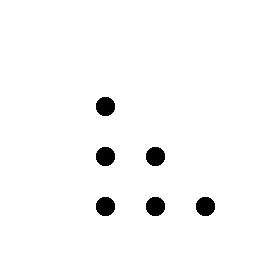3	6	10	...

PROBLEMA 2. El terra d'una de les sales del Monestir de Poblet està recobert per peces quadrades i peces hexagonals formant el mosaic que veus a continuació.

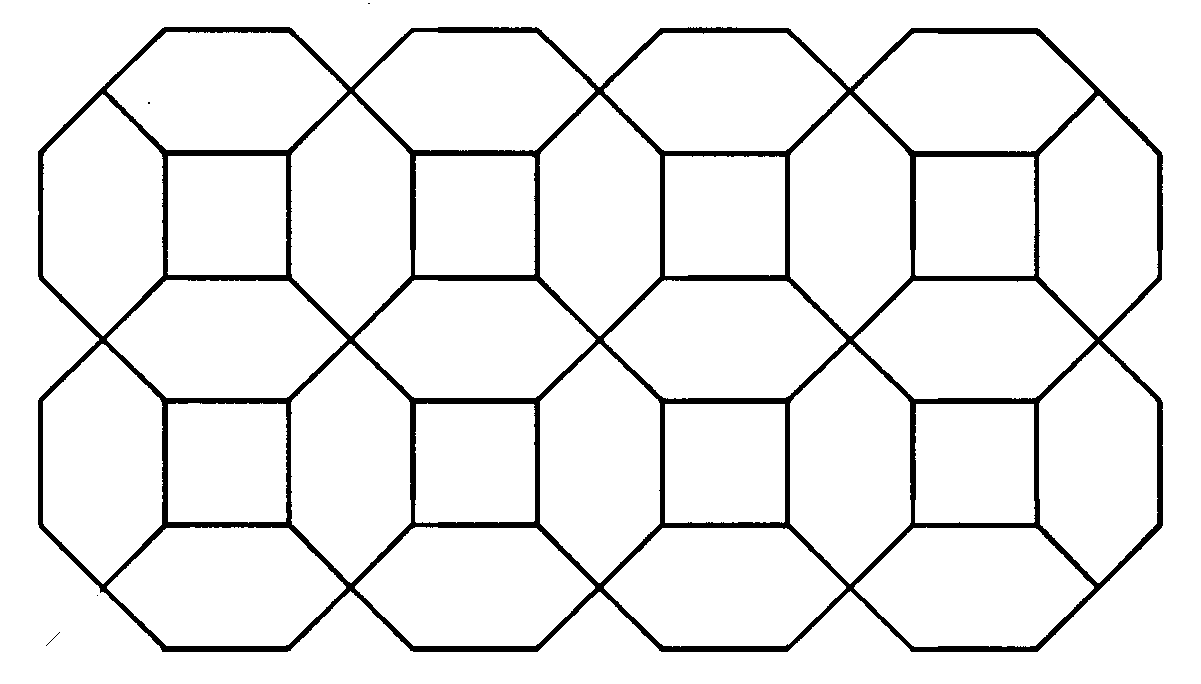
1. Reprodueix aquest mosaic en un paper puntejat de malla quadrada fins ocupar tot el full
2. Quina relació hi ha entre la superfície de les dues peces (triangular i qua-drada)?
3. Si la sala on està col·locat medeix 20 metres de llargada per 12 metres d'amplada, i el costat de la peça quadrada del mosaic medeix 12 cm, quantes peces de cada tipus s'han fet servir per enrajolar el terra?
4. Es vol dissenyar una nova rajola juntant diverses peces d'aquestes (quadrats, hexàgons; enganxant-les només per algun costat comú, sense tallar-les) de manera que amb la nova rajola es pugui fer un mosaic que recobreixi la sala, però ara amb peces totes iguals. Estudia possibles dissenys i per a cadascun d'ells reprodueix en mig full el mosaic que en sortiria.

PROBLEMA 3. Es tracta d'un joc per a dos jugadors. Cadascun dels dos disposa de 15 fitxes (del tipus de les de parxís) que ha de col·locar, com ell vulgui, a les caselles numerades del tauler que s'adjunta.

Llencen alternativament dos daus, i la suma de les puntuacions obtingudes indica la casella de la qual cal retirar una fitxa (si n'hi hagués alguna, però mai no s'ha de retirar més d'una). Guanya el jugador que primer aconsegueix retirar totes les seves fitxes.

Busca la millor manera de col·locar les fitxes i justifica-ho.

PROBLEMA 1. En els claustres de molts monestirs, hi ha una font al centre i quatre altars situats un a cadascun dels quatre vèrtexs del claustre. Hi ha el costum que els fidels, quan vénen a pregar, fan una ofrena de N flors a cada altar. Aquesta N depèn de cada monestir.

Un fidel una mica despistat, no s'havia assabentat de quina era la N del monestir de Poblet, i va venir amb una quantitat escassa de flors, tan escassa que no li arribava ni tan sols per fer l'ofrena de les N flors del primer altar. Tanmateix, Poblet té una llegenda (i si no la tenia, la tindrà a partir d'ara) que diu que si submergeixes a la font les teves flors, un miracle te les dobla en quantitat. Aquest fidel, assabentat d'això, ho fa i efectivament observa com la quantitat de flors que portava se li dobla, amb la qual cosa té suficients flors (N) per poder fer l'ofrena del primer altar i encara en sobren. Però les flors que li queden no són suficients per poder fer l'ofrena del segon altar... i torna a fer el mateix: submeregeix les flors, les dobla i fa l'ofrena al segon altar... I aquest mateix procediment li serveix per poder anar augmentant la seva quantitat de flors i poder fer les corresponents ofrenes de N flors al tercer i quart altar. Tanmateix, els miracles són limitats, i després d'haver efectuat la quarta ofrena observa que ja s'ha quedat definitivament sense flors.

Podríeu dir-nos quantes flors es necessitaven en cada altar (o sigui, N) i amb quantes flors es va presentar el nostre amic al monestir? És possible que arribés amb més de 100 flors i no en tingués prou ni per al primer altar? Què ens podeu dir al respecte? Exploreu a fons la situació.

I si Poblet hagués tingut un claustre pentagonal (i per tant cinc altars)? podríem també esbrinar alguna relació? És possible resoldre ara aquest problema de forma senzilla amb qualsevol forma que tinguin els claustres?

PROBLEMA 2. En un geoplà de 5×5 podem representar-hi nombrosos quadrats, en posicions diferents i amb dimensions diferents. Us demanem que, de forma organitzada, ens digueu en primer lloc quantes dimensions diferents podem representar-hi, i alhora ens compareu les seves superfícies.

A continuació ens direu també per a cadascun d'aquests quadrats, en quantes posicions diferents es poden representar.

Què passaria en un geoplà de 6×6? I en geoplans de grandàries superiors?

PROBLEMA 3. Es tracta d'un joc per a dos jugadors. Cadascun dels dos disposa de 30 fitxes (del tipus de les de parxís) que ha de col·locar, com ell vulgui, a les caselles numerades del tauler que s'adjunta.

LLencen alternativament dos daus, i la suma de les puntuacions obtingudes indica la casella de la qual cal retirar una fitxa (si n'hi hagués alguna, però mai no s'ha de retirar més d'una). Guanya el jugador que primer aconsegueix retirar totes les seves fitxes.

Busca la millor manera de col·locar les fitxes i justifica-ho.

PROBLEMA 1. Com molt bé podeu comprovar,

i no és "massa difícil" observar que "acaba" en dos zeros.

Tanmateix, el resultat de

ja no és tan fàcil de calcular. No us espanteu, només us demanem que esbrineu i argumenteu amb quants zeros "acabarà".

Exploreu també què passa amb altres nombres com el 200, el 500, el 1000, ... i treieu-ne alguna conclusió.

PROBLEMA 2. Tenim un pot cilíndric de 10 cm de diàmetre de la base i 10 cm d'altura. Tenim també un cordill de 30 cm de longitud; creieu que és suficientment llarg per tal que des d'un punt de la circumferència de la tapa pugui donar un tomb sencer al pot (i de manera "uniforme") i arribi al seu punt corresponent (projecció) de la circumferència de l'altra tapa?

Quina és la longitud mínima perquè això pugui passar? I quina és la longitud mínima per aconseguir envoltar-lo des d'un punt a l'altre donant abans dos tombs (de manera uniforme) al pot?

Exploreu aquesta situació establint relacions entre la longitud del fil i el nombre de tombs. Exploreu també què passaria amb pots que tinguessin formes diferents a la del cilindre.

PROBLEMA 3. Cada vegada que visitem el monestir de Poblet ens donen aleatòriament un sobre que conté una lletra de la paraula P-O-B-L-E-T; així, al cap de 6 vegades de visitar-lo hem pogut tenir la grandíssima sort d'haver acumulat exactament les 6 lletres diferents, però també pot haver passat que haguem acumulat 6 lletres L,… o moltes possibilitats més. El cas és que quan aconsegueixes reunir com a mínim les 6 lletres (P, O, B, L, E, T) et regalen una entrada gratuïta vitalícia als tres monestirs de la Ruta del Císter.

Quantes visites creieu que és "convenient" fer a Poblet per tal de poder reunir les 6 lletres? Estudieu a fons aquesta situació.