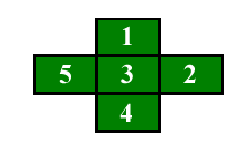

a) Intenteu disposar els mateixos nombres de manera que la suma total de la fila sigui igual a la de la columna. Amb aquesta condició, quina és la suma de la fila (o columna) més gran possible que podeu trobar? I la suma total de la fila (o columna) més petita possible? Expliqueu perquè els nombres parells no es poden col·locar en el quadrat central.
b) Escriviu uns altres cinc nombres consecutius i penseu que els disposeu de manera que la suma de la fila i la suma de la columna siguin iguals. Quina és la suma total de la fila (o columna) més gran que podeu trobar en aquestes condicions amb els nombres que heu escrit? Quina és la suma més petita, ara?
Ara imagineu que una altra persona escriu cinc nombres consecutius. Intenteu explicar quines operacions hauríeu de fer amb aquests nombres per deduir quina és la suma total més gran de la fila (coincident amb la de la columna) que podeu trobar amb aquests números. Expliqueu també com calcularíeu la suma més petita. Expliqueu perquè els totals més gran i més petit sempre tenen una diferència de dos.
PROBLEMA 2. A) Dibuixeu un rectangle de 10 cm de llarg i 6 d’ample, i traceu una de les seves diagonals. Retalleu els dos triangles obtinguts. Amb els dos triangles, fent que coincideixin completament dos costats iguals i sense superposar-los, podeu formar diferents figures. En el gràfic següent teniu un exemple; però fet a partir d’un quadrat.
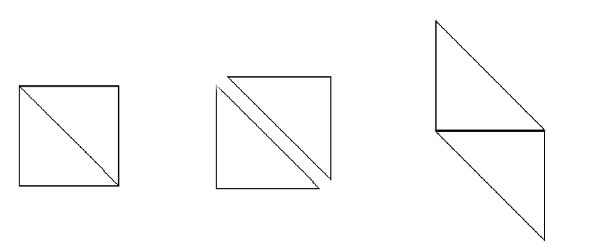
a) Quantes figures diferents podeu formar?
b) Quina de les figures té el perímetre més gran? Quant val aquest perímetre?
c) Quina de les figures té el perímetre més petit? Quant val aquest perímetre?
d) Què podeu dir de les àrees de les figures construïdes?
B) Dibuixeu un triangle qualsevol (que no sigui ni rectangle ni isòsceles). Dividiu-lo
en tres parts de manera que amb elles es pugui formar un rectangle. És possible ferho
de més d’una manera?
PROBLEMA 3. Tenim un tauler format per cinc hexàgons regulars iguals, com el que es veu a la figura.
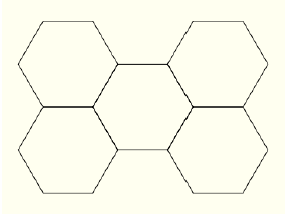
Dos jugadors, al seu torn, van posant una peça a cada jugada per recobrir els hexàgons. Cada peça es posa dins d’un hexàgon. El guanyador de la partida és el jugador que aconsegueix col·locar l’última peça, de manera que després d’aquesta jugada el tauler queda completament recobert.
Hi ha tres tipus de peces: Trapezis isòsceles (equivalents a mig hexàgon), rombes (equivalents a un terç d’hexàgon) i triangles equilàters (equivalents a un sisè d’hexàgon). El nombre de peces de cada tipus és il·limitat.
Practiqueu el joc i digueu qui te avantatge, el primer o el segon jugador. Trobeu una manera de jugar que asseguri a un dels jugadors la possibilitat de guanyar.
PROBLEMA 1. Dues granotes i dos gripaus estan en una filera de cinc quadrats. (Les granotes són els cercles negres, els gripaus els cercles blancs.)

Les granotes i els gripaus volen intercanviar les seves posicions. Per fer-ho avancen un quadrat

o salten sobre un animal de l’altre espècie (les granotes salten per sobre un gripau i els gripaus sobre una granota).

Explica com poden intercanviar-se les posicions dels gripaus i les granotes. Quin serà el mínim nombre de moviments necessari?
Fes el mateix amb tres granotes i tres gripaus sobre una filera de set quadrats.

Quin serà ara el mínim nombre de moviments per intercanviar les posicions?
PROBLEMA 2. La Maria té cubs de color roig, de color groc, de color blau i de color verd. Vol construir un cub més gran, com el del dibuix.
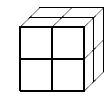
La Maria vol que a cada cara del cub gran hi hagi hi hagi un quadrat de cada color.
Com ho farà? De quantes maneres diferents pot construir el cub?
PROBLEMA 3. L’Elisabet va comprar un llibre de matemàtiques que valia exactament 5 euros. No tenia cap bitllet per`o portava moltes monedes a la butxaca. Es va adonar, de tota manera, que no podia pagar exactament els 5 euros que li demanaven. Podia pagar
altres quantitats, com 5,01 euros, però no exactament 5.
Quants diners podia portar en total? Quina és la quantitat màxima de diners que podia dur?
PROBLEMA1.
En un jardí quadrat de 30 m de costat hi ha plantats dos arbres, que anomenarem A i B, exactament en dos vèrtexs contigus del quadrat. Ara, volem plantar altres arbres en aquest jardí amb les condicions següents:
• Tots els arbres nous han d’estar a la mateixa distància de l’arbre A que de l’arbre B.
• La distància dels nous arbres als arbres A i B ha de ser un nombre enter de metres.
a) Quin és el nombre màxim d’arbres que podrem plantar? Creieu que un arbre nou, és a dir dels que hem plantat, està situat a la mateixa distància dels dos arbres nous que té més a prop?
b) Si per prendre mides disposem d’una corda llarga que té un nus a cada metre, com trobaríem la posició exacta on hem de plantar cada arbre?
c) Considereu ara tots els triangles formats pels dos arbres inicials, A i B, i cadascun del arbres plantats de nou. Quants d’aquests triangles són obtusangles?
És possible que algun d’aquests triangles sigui rectangle? Per què?
PROBLEMA 2.
La figura mostra un rectangle que està format per 5 quadrats. Ho hem fet dibuixant primer el quadrat A i després, a baix el B, a l’esquerra el C, a sobre el D i a la dreta l’E.
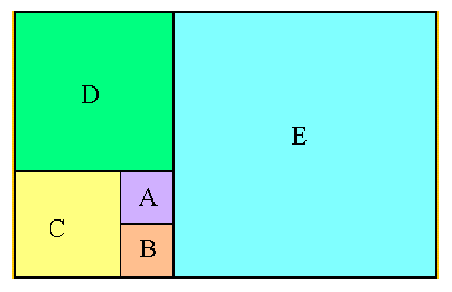
a) Suposant que l'àrea de tot el rectangle és de 40 cm2, calcula l'àrea de cadascun dels quadrats petits.
b) Quina seria l’àrea de tot el rectangle, si el quadrat A tingués el costat igual a 2?
c) Quin seria el costat del primer quadrat si l'àrea del rectangle fos 16000?
d) La figura donada es pot continuar afegint cada vegada un quadrat de més, primer a baix, que tingui com a costat el que ara és la base del rectangle; després a l’esquerra, que tingui com a costat el que llavors seria l’altura del rectangle; i continuant amb altres quadrats a dalt, a la dreta i així successivament. Escriu les longituds dels costats dels quadrats de la figura de l’enunciat de més petit a més gran i digues quines serien les longituds dels costats dels cinc quadrats següents.
e) Quina seria la longitud del costat del vuitè quadrat si la del primer fos 3?
PROBLEMA 3.
Sobre un tauler d’escacs es situa una reina en una casella qualsevol de la primera fila (fila superior) o de l’última columna (columna de la dreta) excepte en les caselles dels vèrtexs.
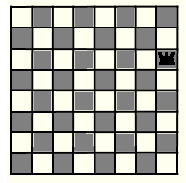
Al seu torn, cadascun dels dos jugadors va movent la reina tantes caselles com vulgui, horitzontalment (cap a l’esquerra), verticalment (cap avall), o en diagonal (cap a l’esquerra i cap avall). El jugador que aconsegueixi situar la reina en la casella inferior esquerra del tauler és el guanyador de la partida.
Vegeu un exemple de partida en què guanya el segon jugador (el groc)
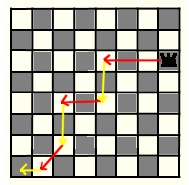
Practiqueu el joc i digueu qui te avantatge, el primer o el segon jugador. Trobeu una manera de jugar que permeti guanyar sempre a un dels dos jugadors.
L’estratègia que heu dissenyat, val igual sigui la que sigui la casella on s’ha
situat inicialment la reina?