GEOMETRIA ANALÍTICA PLANA:
punts i rectes
|
|
Equacions de la recta
Equació vectorial d’una recta
Equació vectorial de la recta que passa
per A=(0,4) i de direcció u=(3,2)
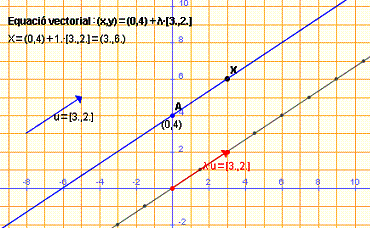
Si X és
un punt de la recta que passa per A i de direcció u, X és el traslladat de A
segons un vector múltiple del vector u
Per tant, les coordenades del punt X(x ,y) verifiquen l’equació:
Observa que el punt (3,6) és un punt de la recta i s’obté per l=1.
Podem fer un raonament semblant per la recta que passa per un punt qualsevol A(a1, a2) i té per direcció u=(u1, u2)
Si X és un punt d’aquesta recta, X és el traslladat de A segons un vector múltiple de u, l·u, per tant les coordenades (x, y) de X verifiquen:
E 1 Equació vectorial
Fes els exercicis següents al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
· En una pantalla de la Wiris podràs moure l’extrem del vector l·u i observar com varien les coordenades dels punts X de la recta.
Obra el document equació vectorial. Escriu a la teva llibreta cinc punts més d’aquesta recta
Després mou el punt A i fixa’t si varia l’equació vectorial. Anota al teu quadern tot el que hagis observat
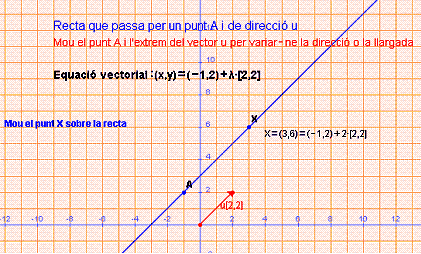
· En una altra pantalla podràs canviar tant el punt com la direcció de la recta. Escriu l’equació vectorial de tres rectes. Per cadascuna d’elles dóna tres punts. Per cada punt, indica el valor del paràmetre l. Obra equació vectorial 2 .
· Escriu l’equació vectorial de la recta que passa per (-1,2) i (3,7)
· Comprova si els punts (5,-13) i (-5,12) són de la recta que passa per (1,-3) de direcció (-2,5)
Pendent d’una recta
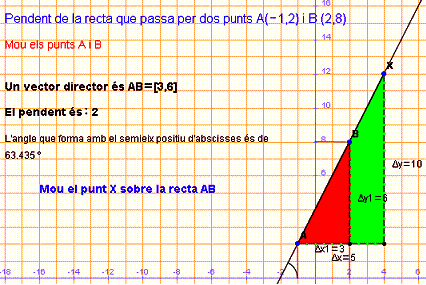
Pendent de la recta que passa per A(-1,2)
i B=(2,8)
Si X és un punt
de la recta que passa per dos punts A i B, els components del vector AX i els
del vector AB són proporcionals; la proporció entre l’ordenada i l’abscissa d’aquests
vectors s’anomena pendent de la recta AB. Aquest valor coincideix amb la
tangent de l’angle que forma la recta amb el semieix positiu d’abscisses.
El pendent de la recta que passa per A(-1, 2) i B(2, 8) és
Fes els exercicis següents al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
· Investiga amb la finestra pendent .
· Una recta té de pendent 2. Un vector director d’aquest recta és_____________
· Una recta té de pendent -3. Un vector director d’aquest recta és_____________
· Si un vector director és (2, 8), el pendent és: ______________
· Si un vector director és (-2, 8), el pendent és: ______________
· Quina relació hi ha entre els pendents de dues rectes paral·leles?
· Calcula un vector director de la recta que passa per A(-1,2) i B(2,4)
· Calcula el pendent de la recta que passa per A(-1,2) i B(2, 4)
·
Completa: El pendent de la recta que
passa per A(a1, a2) i B(b1, b2) és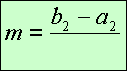 
Equació contínua d’una recta
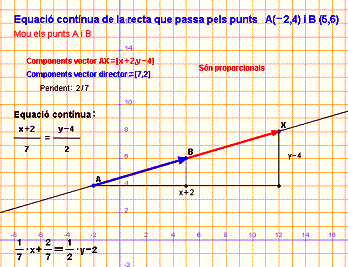Equació contínua de la recta que passa per A=(-2,4)
i per B=(5,6)
Volem escriure una condició que han de verificar els punts X(x ,y) per pertànyer a la recta r que passa per A(-2,4) i B(5,6)
Un vector director de r és u = AB = (5+2,6-4)=(7, 2).
Si X és un punt d’aquest recta, els components del vector AX i els de u són proporcionals.
Per tant, es verifica: 
, 
que és l’equació
contínua de r
Aquesta equació també es pot escriure així: 
Podem fer el mateix raonament per la recta que passa per dos punts qualsevol A(a1, a2) i B(b1, b2)
Si X és un punt de la recta que passa per A i B, els components del vector AX i els de AB són proporcionals.
Per tant podem escriure
E2. Equació contínua
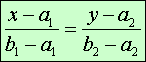
on els numeradors són els components del vector AX i el denominador les del vector AB o qualsevol vector directors de la recta.
Fes els exercicis següents al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
· Investiga a la finestra contínua.
· Comprova que el punt P(3/2, 5) és de la recta r que passa per A(-2,4) i B(5,6)
· Comprova que el punt Q(0, 4) no pertany a la recta r passa per A(-2,4) i B(5,6)
· Escriu l’equació contínua de la recta que passa per A(-3,6) i B(12, 5)
· Escriu l’equació contínua de la recta que passa per A(-6, 0) i de direcció u=(-2,3)
Equació explícita
Equació explícita de la recta que passa
per A(-2,4) i B(5,6)
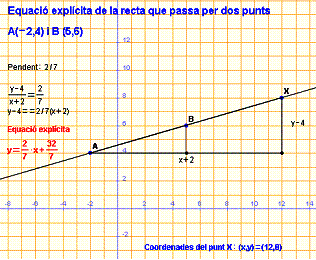
En l’equació
contínua d’aquesta recta, 
, aïllem y-4, 
;
i si després aïllem
y, obtenim 
que és l’equació
explícita de la recta.
Finalment operem, 
En general, partim de
l’equació contínua de la recta que passa per A(a1, a2) i
B(b1, b2); I com a l’exemple, aïllem y- a2 de
l’equació contínua 
,
, 
,
i si indiquem per m al pendent d’aquesta recta 
; aïllem y
E3. Equació explícita
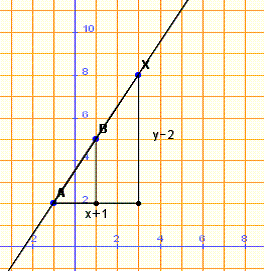
També podem arribar a aquesta equació explícita de la recta fent un altre raonament:
La recta de la figura adjunta té de pendent 
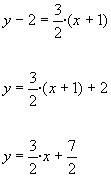
Així, la
recta de pendent m que passa per A(a1, a2) verifica 
, i en resulta 
Fes els exercicis següents
al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
· Investiga a la finestra explícita.
· Escriu l’equació explícita de la recta que passa per (0, -3) i (4, 1)
· Escriu el pendent i l’equació explícita de les rectes que passen per
a) A(0,0) i B(3,6)
b) A(-1,2) i B(1,5)
· Escriu l’equació explícita de tres rectes. Dóna tres punts de cadascuna d’elles.
· Comprova si els punts (-1,2), (1,5) i (5,11) estan alineats.
· I els punts (-1,3), (1,4) i (5,8) ?
· Totes les rectes tenen l’equació explícita?
Equació general
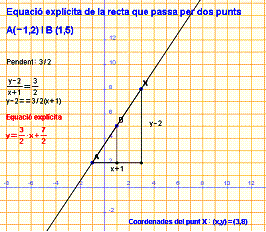
Equació general de la recta que passa per
A(-1,2) i B(1,5)
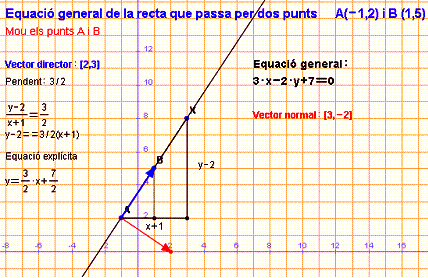En l’equació contínua d’aquesta recta, 
, si multipliquem en creu obtenim 
, i si operem i traspassem tots els termes al membre
esquerra,
, 
que és l’equació
general de la recta
En general,
partim de l’equació contínua de la recta que passa per A(a1, a2) i B(b1, b2) i si indiquem per u el vector AB,
u=(u1, u2)=(b1-a1,b2-a2),
Multipliquem amb creu 
Traspassem els termes 
i si operem 
, equació que és de la forma:
E4. Equació general
Els coeficients a i b d’aquesta equació proporcionen el vector director de la recta: (-b,a). I (a,b) és un vector perpendicular a la recta
Fes els exercicis següents al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
· Obre la finestra general Mou els punts A i B i observa com varien les equacions generals de la recta.
·
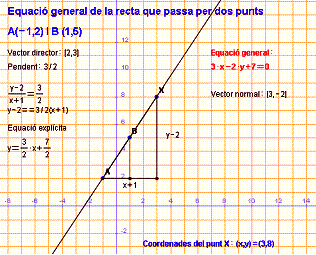Escriu l’equació general de les
rectes que passen per
a) A(0,0) i B(3,6)
b) A(-1,2) i B(1,5)
· Escriu l’equació general de dues rectes. Dóna dos punts de cadascuna d’elles.
·
Escriu l’equació general de les rectes
següents: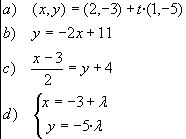 
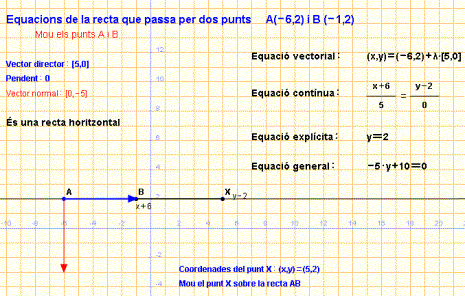
Les equacions d’una recta
Es poden obtenir les diferents equacions d’una recta a partir de dos punts, d’un punt i el pendent, d’un punt i un vector director o d’un punt i el vector normal.
Caldrà que pensis en cada cas el camí més adequat per obtenir les equacions. Hi ha moltes maneres de fer-ho, només cal vigilar en no equivocar-se amb els signes i les operacions. És molt convenient comprovar les equacions amb les dades inicials.
Per exemple,
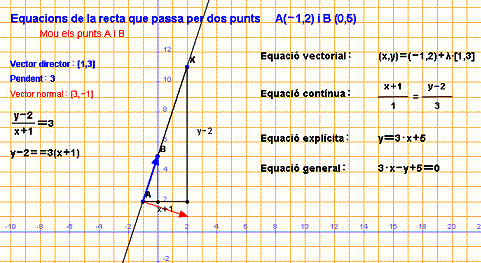
Equació vectorial de la recta que passa per A(-1,2) de
pendent 3.
Un vector director d’aquesta recta és (1,3);
una equació vectorial és 
Equació explícita de la recta que passa per A(-1,2) de pendent 3.
Si utilitzes el concepte de pendent d’una
recta: 
i per tant, 
O bé, de 
obtens 
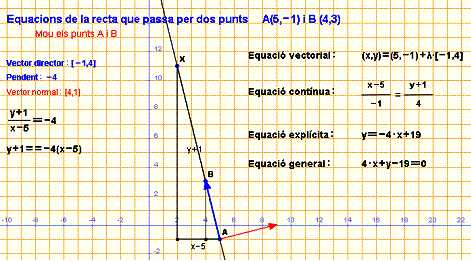
Equació general de la recta que passa per A(-1,2) i vector
normal(3,-1)
Recorda que els coeficients á i b d’aquesta
equació són justament els components d’un vector normal, per tant, 
, 
, 
Fes els exercicis següents al teu quadern. Les finestres de la Wiris que podràs obrir et
facilitaran la tasca. Quan acabis els exercicis, tanca les finestres i continua
amb els següents apartats.
·
Obre la finestra equacions_recta.
Mou els punts A i B i observa com varien les equacions de la recta
|
|
|
|
|
|
· Equació vectorial de la recta que passa per (2,-3) i té per pendent -2
· Equació general de la recta que passa per (-1,0) i de direcció (2,-3)
· Equacions de la recta que passa per (-2,1) i (2,-5)
· Equacions de la recta que passa per (0,-4) i de vector normal (2,5)
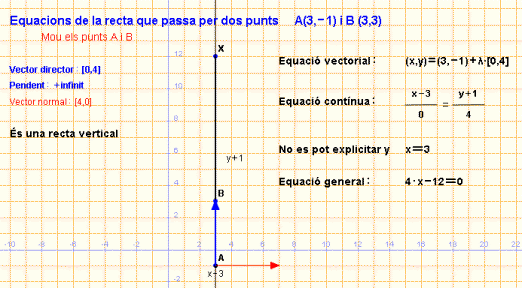
· Escriu totes les equacions d’una recta vertical
· Com podries esbrinar que dues equacions vectorials representen la mateixa recta?
· Fes un resum de les equacions de les rectes. Comprova amb un company els vostres resums.
Posició relativa de punts i rectes
Posició relativa d’un punt i una recta
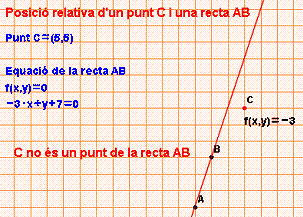Quina és la posició relativa dels punt C=(5,5),
D=(3,2) i la recta -3x+y+7=0?
El punt C no verifica l’equació de la recta, 
, per tant, C no és un punt d’aquesta recta
El punt D verifica l’equació, -3·3+2+7=0, per tant, D és un punt de la recta -3x+y+7=0
|
Posicions relatives d’un put
C respecte una recta r |
C no és un punt de la recta |
· Obre la finestra punt_recta Mou els punts A, B i C i observa si el punt C pertany a la recta AB.
· Investiga la posició relativa dels punts (2,3) i (3,0) respecte la recta 2x-3y+6=0.
· Escriu l’equació d’una recta i dóna tres punts d’aquesta recta i tres punts fora de la recta
Equació de la recta paral·lela que passa per un punt
Equació de la recta paral·lela a y = 2/3·x -2 que passa per C=(3,4)
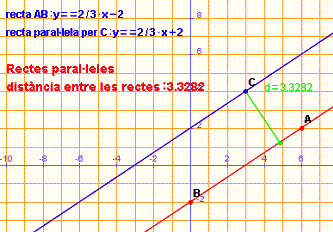
Les rectes paral·leles tenen el mateix pendent, per tant la recta que busquem té per pendent m= 2/3 i passa per C
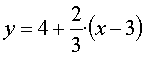
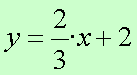
La paral·lela a 
que passa per 
és 
Fes els exercicis següents al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
· Obre la finestra paral·lela 1 Mou els punts A i B i observa les equacions de la recta r i la seva paral·lela
·
Escriu l’equació explícita de la
recta paral·lela a 
que passa per (2,-6)
· Escriu l’equació explícita de la recta que passa per (-1,3) i és paral·lela a la recta que passa per (1,2) i (-4,7 )
Equació de la recta paral·lela a -2·x+3·y+4 = 0 que passa per C=(3,5)
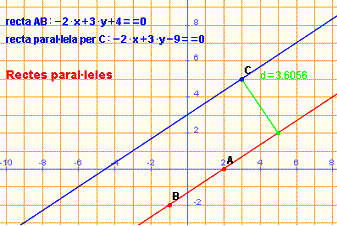
La recta paral·lela té el mateix vector normal i passa per C:
La paral·lela a 
que passa per 
és 
Fes els exercicis següents al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
· Obre la finestra paral·lela 2 Mou els punts A i B i observa les equacions de la recta r i la seva paral·lela
·
Escriu l’equació general de la recta paral·lela a 
que passa per (2,-6)
· Escriu l’equació general de la recta que passa per (-1,3) i és paral·lela a la recta que passa per (1,2) i (-4,7 )
Has
vist que les equacions generals de dues rectes paral·leles tenen els
coeficients de x i de y iguals o proporcionals.
són coincidents si 
són paral·leles si 
Equació de la recta paral·lela a (x,y) = (1,0) + l·(-2,-2)
que passa per C=(3,5)
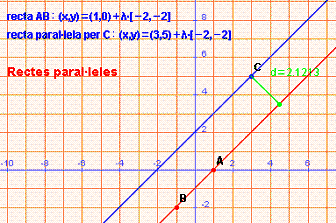
La recta paral·lela té el mateix vector director i passa per C:
La paral·lela a 
que passa per 
és 
Fes els exercicis següents al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
· Obre la finestra paral·lela 3 Mou els punts A i B i observa les equacions de la recta r i la seva paral·lela
·
Escriu l’equació vectorial de la recta
paral·lela a 
que passa per (2,-6)
· Escriu l’equació general de la recta que passa per (-1,3) i és paral·lela a la recta que passa per (1,2) i (-4,7 )
|
|
Tenen
el mateix pendent Els
mateixos vectors directors Els
mateixos vectors normals |
Intersecció de dues rectes secants
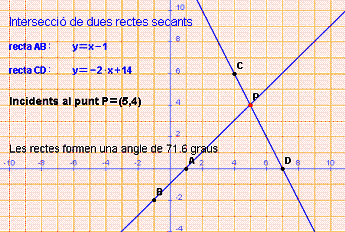
Dues rectes del pla són secants si no tenen la mateixa direcció. Les rectes secants tenen un punt en comú. Es pot obtenir resolent el sistema format per les equacions de les rectes. El càlcul que s’ha de fer depèn de les equacions de les rectes. És preferible utilitzar les equacions explícites o les generals.
Punt intersecció de les rectes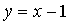 
i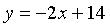 
Resolem el sistema 
Aquestes rectes tenen un punt en comú, P=(5, 4)
Punt intersecció de les rectes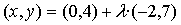 
i 
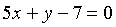
Equació general de 
, 
(També podries
escriure primer la contínua i multiplicar en creu)
Resolem el sistema 
Aquestes rectes tenen un punt en comú, P=(2, -3)
Fes els exercicis següents al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
·
Obre la finestra secants
Mou els punts A, B, C i D i observa com varien les equacions de les recta i el
seu punt comú
·
Troba el punt comú a les rectes 
i 
·
Troba el punt comú a les rectes 
i 
·
Punt comú de la recta que passa per
(-2,-1) i (10,-3) i la recta que passa
per (1,-3) i (7,-1)
|
|
Tenen
un punt en comú No tenen
el mateix pendent No
tenen els mateixos vectors directors |
Posició relativa de dues rectes en el pla
Per saber la posició relativa de dues rectes cal resoldre el sistema format per les seves equacions
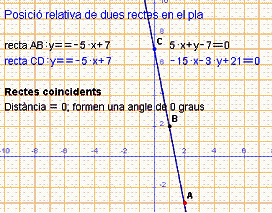Punt intersecció de les rectes 
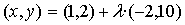i 
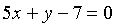
Equació general de 
, 
(També podries
escriure primer la contínua i multiplicar en creu)
Resolem el sistema 
Aquestes
rectes són coincidents
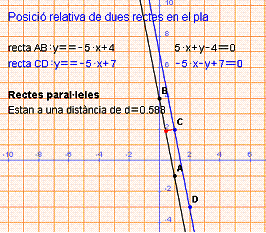Punt intersecció de les rectes 
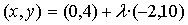i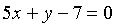 
Equació general de 
, 
Resolem el sistema 
Aquestes rectes no tenen cap punt en comú, i com que tenen igual direcció, són paral·leles
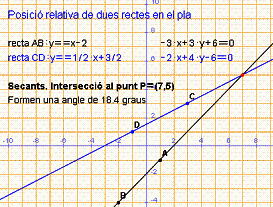
Punt intersecció de les rectes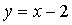 
i 
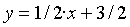
Resolem el sistema 
Aquestes
rectes són secants. El punt comú és (5, 7)
Fes els exercicis següents al teu quadern. Les finestres de
la Wiris que podràs obrir et facilitaran la tasca. Quan acabis els exercicis,
tanca les finestres i continua amb els següents apartats.
·
Obre la finestra posició
relativa Mou els punts A, B, C i D i observa com varien les
equacions de les recta i la seva posició relativa
·
Estudia la 
i 
·
Posició relativa de les rectes a les rectes 
i 
· Escriu l’equació de dues rectes secants, dues rectes paral·leles i dues rectes coincidents.
· Escriu l’equació de tres rectes que no tinguin cap punt en comú, però cada dues siguin secants, és a dir, les tres rectes han de formar un triangle.
|
|
Coincidents. Tots els punts en comú Secants. Un punt en comú Paral·leles. Cap punt en comú |
A
partir de les equacions generals de les rectes el criteri és molt senzill:
són coincidents si 
són paral·leles si 
són secants si 
Annex: Problemes sobre vectors
Vectors perpendiculars i del mateix mòdul que un vector donat
Segur que sabries representar el vector u=(2,4) i vectors que siguin perpendiculars a u. N’hi ha molts!
· Representa el vector u=(2,4). Dibuixa una recta perpendicular a aquest vector. Quina direcció té aquesta recta?
· Escriu els components de tres vectors que siguin perpendiculars a u.
· Escriu els components dels vectors perpendiculars i del mateix mòdul que u.
· Si no ho veus clar o si vols comprovar el resultat, obre la finestra perpendiculars
Troba els altres vèrtexs d’un quadrat a partir de dos vèrtexs consecutius
· Dibuixa el segment d’extrems A= (-2, -1) i B=(1, 4). Dibuixa un quadrat de costat AB. Quants en pots dibuixar?
· Calcula les coordenades dels vèrtexs C i D d’un quadrat ABCD amb A=(-2,-1) i B=(1, 4)
· Comprova el resultat a la finestra quadrat
· Com faries el problema si els vèrtexs donats estiguessin en diagonal?
Calcula l’àrea d’un paral·lelogram, coneguts dos vèrtexs consecutius i la recta que conté els altres dos
· Dibuixa el segment d’extrems A(0,0) i B=(6,2). Construeix sobre aquest segment un paral·lelogram.
· Calcula l’àrea d’un paral·lelogram ABCD, sabent els vèrtexs A=(0,0) i B=(6,2) i que C i D estan en una recta que passa per M=(-6,5)
· Comprova el resultat a la finestra paral·lelogram
