D122. Mòdul 6. Exercicis. Dibuix tècnic amb l'AutoCAD

Figura 1. Vista tridimensional amb ombrejat Gouraud, planta i alçat de la figura que s'ha de fer

Figura 3. Matriu polar de les línies i l'arc anteriorment creats

Figura 4. Contorno intern i extern mitjançant un cercle concèntric

Esborreu el cercle, les línies i el arcs que heu fet servir per fer el contorn, i dibuixeu un nou parell de cercles concèntrics de radis 40 i 20 unitats de dibuix amb centre a 100,100, i una línia múltiple justificada a Cero i amb Escala 10 entre dos quadrants, tal i com mostra la figura 6.

Figura 7. Matriu polar de la línia múltiple feta anteriorment

Figura 8. Regions de A a F creades amb l'eina Contorno desplaçades fins a ser concèntriques amb la regió de la roda dentada

Figura 9. Regions de A a G inscrites dins la regió de la roda dentada

Figura 10. Regió de la roda dentada menys regions de A a G, vist amb un ombrejat Gouraud

Figura 12. Alçat, planta, perfil i vista isomètrica SO amb ombrejat Gouraud de la figura proposada

Figura 13. Polilínia feta des de la vista isoplana esquerra

Figura 14. Segona polilínia, vista des de la vista isoplana superior

Figura 16. Dues polilínies 2D vistes des de la perspectiva isomètrica SO

Figura 17. Dos cercles amb centre als extrems de la primera i segona polilínia

Figura 18. Extrusió dels dos cercles sobre les polilínies

Figura 19. Còpia i desplaçament dels sòlids

Figura 20. Resultat definitiu, vist amb ombrejat de filferro 2D i Gouraud

Figura 23. Pas de l'eix de revolució i resultat corresponent amb ombrejat Gouraud i punt de vista isomètric SO

Figura 24. Pas de l'eix de revolució i resultat corresponent amb ombrejat Gouraud i punt de vista isomètric SO

Figura 25. Pas de l'eix de revolució i resultat corresponent amb ombrejat Gouraud i punt de vista isomètric SO

	Per tal de consolidar els coneixements adquirits durant el present mòdul, heu de fer els exercicis 1, 2 i 3. L'exercici 4 és optatiu.

	Exercici 1: practicar els contorns, les regions i l'extrusió simple

	A continuació, treballareu de manera guiada les eines Contorno, Región i Extrusión, per aconseguir una figura sòlida com la que mostra la imatge següent:


	Figura 1. Vista tridimensional amb ombrejat Gouraud, planta i alçat de la figura que s'ha de fer

	En primer lloc, obriu un document nou de característiques habituals i immediatament guardeu-lo com a identificador de la xtec_m6_ex01.dwg

	Ara feu el contorn extern de la figura (la roda dentada): Feu dos cercles concèntrics de radi 50 i 60 unitats de dibuix, amb centre a la coordenada 100,100. A continuació, feu dues línies de 60 unitats de dibuix de longitud amb origen a 100,100, una d'elles orientada cap a 0º, @60<0, i l'altra amb 15º respecte a la primera, @60<15. Després, feu servir l'eina Recorta per deixar esborrar el cercle exterior exceptuant l'arc comprès entre les dues línies, tal com mostra la figura següent:

	Figura 2

	Ara feu una matriu polar de les línies i l'arc de 15º amb centre 100,100 amb un total de 12 ítems que seran les 12 dents de la roda dentada, que ocupin la totalitat del 360º i que girin sobre 100,100 a mesura que són creats:


	Figura 3. Matriu polar de les línies i l'arc anteriorment creats
	A continuació feu un cercle concèntric de radi major al de la figura obtinguda i feu un contorn amb mètode Inundación i tipus d'objecte Polilínea, fent clic tal i com mostra la figura 4:


	Figura 4. Contorno intern i extern mitjançant un cercle concèntric
	Esborreu el cercle exterior i la polilínia que se li superposa i desplaceu la polilínia resultant del perímetre intern, tal i com mostra a la figura 5. Després, transformeu-la en una regió amb l'ordre Región.


	Figura 5. Resultat del Contorno intern anteriorment realitzat

	Esborreu el cercle, les línies i el arcs que heu fet servir per fer el contorn, i dibuixeu un nou parell de cercles concèntrics de radis 40 i 20 unitats de dibuix amb centre a 100,100, i una línia múltiple justificada a Cero i amb Escala 10 entre dos quadrants, tal i com mostra la figura 6.

	Figura 6
	Feu una matriu polar de tres elements rotats sobre 100,100 amb la línia múltiple, tal i com mostra la figura següent:


	Figura 7. Matriu polar de la línia múltiple feta anteriorment

	Ara feu un contorn amb mètode Inundación i tipus d'objecte Región, per obtenir sis regions com les següents -equivalents als espais buits interiors de la roda dentada-, i desplaceu-los fins al centre de la regió anteriorment creada (la roda dentada):


	Figura 8. Regions de A a F creades amb l'eina Contorno desplaçades fins a ser concèntriques amb la regió de la roda dentada

	Esborreu-ho tot menys la roda dentada i les regions de A a F, feu un cercle concèntric (G) a aquesta de radi 10 i transformeu-lo en una regió (amb l'ordre Región):


	Figura 9. Regions de A a G inscrites dins la regió de la roda dentada

	Ara feu una operació booleana de sostracció de regions (odre Diferencia); a la regió de la roda dentada resteu les regions de la A a la G. Comproveu si això realment s'ha fet, observant l'espai de dibuix amb un ombrejat Gouraud:


	Figura 10. Regió de la roda dentada menys regions de A a G, vist amb un ombrejat Gouraud
	Visualitzeu l'espai de dibuix des d'una persepectiva isomètrica qualsevol -per exemple, SO- i, per últim, executeu una extrusió simple de 20 unitats de dibuix (ordre Extrusión). Obtindreu l'objectiu desitjat per a aquest exercici:


	Figura 11

	Exercici 2: practicar l'extrusió amb recorregut

	A continuació, treballareu l'extrusió amb recorregut, per aconseguir una figura com la següent:


	Figura 12. Alçat, planta, perfil i vista isomètrica SO amb ombrejat Gouraud de la figura proposada

	En primer lloc, obriu un document nou de característiques habituals, i immediatament deseu-lo com a identificador de la xtec_m6_ex02.dwg

	Ara feu la polilínia corresponent a l'estructura principal de l'escaleta. En primer lloc, seleccioneu la vista isoplana esquerra, menú Ver\|Pto. vista 3D\|Izquierdo, i feu una polilínia de les mesures següents:


	Figura 13. Polilínia feta des de la vista isoplana esquerra

	A continuació, des de la vista isoplana superior, menú Ver\|Pto. vista 3D\|Superior, feu una segona polilínia amb origen a la referència a objectes fin de la primera polilínia, amb les mesures següents:


	Figura 14. Segona polilínia, vista des de la vista isoplana superior

	A continuació visualitzeu l'espai de dibuix des de la perspectiva isomètrica SO, tal i com mostra la figura següent:


	Figura 15

	Ara gireu la icona SCP 90º sobre l'eix X tal i com mostra la imatge següent:

	Figura 16. Dues polilínies 2D vistes des de la perspectiva isomètrica SO
	Ara dibuixeu dos cercles de radi 2,5 unitats de dibuix, un amb centre en un extrem de la primera polilínia i l'altre amb centre en un extrem de la segona, tal com mostra la imatge:


	Figura 17. Dos cercles amb centre als extrems de la primera i segona polilínia

	Ara extrudiu els cercles sobre les corresponents polilínies amb l'ordre Extrusión:


	Figura 18. Extrusió dels dos cercles sobre les polilínies

	Copieu i desplaceu el sòlid vertical 40 unitats de dibuix sobre les X -@40,0- i desplaceu l'altre sòlid -5 unitats de dibuix sobre les Y -@0,-5 :


	Figura 19. Còpia i desplaçament dels sòlids

	Feu una còpia múltiple del sòlid central, deixant entre l'una i l'altra una distància de 20 unitats de dibuix -primera còpia a @0,-20; segona a @0,-40, tercera a @0,-60 i quarta a @0,-80 :


	Figura 20. Resultat definitiu, vist amb ombrejat de filferro 2D i Gouraud

	Uniu els diferents objectes en un únic sòlid amb la booleana Unión.

	Exercici 3: practicar la revolució

	A continuació, treballareu la revolució per aconseguir tres figures com les següents:


	Figura 21

	Obriu un document nou de característiques habituals, deseu-lo a la carpeta Exercicis amb el nom identificador de la xtec_m6_ex01.dwg i feu una polilínia de les mesures següents:


	Figura 22

	A continuació, copieu dues vegades la polilínia, de manera que tindreu tres polilínies que correspondran als tres objectes.

	Primer objecte de revolució

	Executeu l'ordre Revolución. A Designe objetos: seleccioneu la primera polilínia i premeu la tecla de Retorn. A Precise punto inicial de eje de revolución o defina eje mediante [Objeto/Abcisas/oRdenadas]: escriviu cer, premeu la tecla de Retorn, i feu clic sobre un punt qualsevol del costat dret de la figura -el de 150 unitats de dibuix. A Precise punto final del eje escriviu de nou cer, premeu la tecla de Retorn i feu clic en un altre punt qualsevol de la mateixa línia. Per últim, a Precise ángulo de revolución <360> premeu la tecla de Retorn. El resultat és aquest:


	Figura 23. Pas de l'eix de revolució i resultat corresponent amb ombrejat Gouraud i punt de vista isomètric SO

	Segon objecte de revolució

	Repetiu l'operació amb la segona polilínia, però ara seleccioneu com a eix de revolució el costat superior, tal com s'indica en la figura següent:


	Figura 24. Pas de l'eix de revolució i resultat corresponent amb ombrejat Gouraud i punt de vista isomètric SO

	Tercer objecte de revolució

	Per últim, repetiu l'operació amb la tercera polilínia, però ara seleccioneu com a eix de revolució dos punts externs a la figura, paral·lels a l'eix Y i a 20 unitats de dibuix de l'extrem esquerre de la polilínia, i revolucioneu-la només 90º en sentit antihorari. El resultat és el següent:


	Figura 25. Pas de l'eix de revolució i resultat corresponent amb ombrejat Gouraud i punt de vista isomètric SO

	Exercici 4 (optatiu)

	Feu un objecte 3D utilitzant les eines estudiades al llarg del present mòdul. Per fer l'objecte ràpidament i correctament, procureu organitzar-vos bé la feina: Primer, feu tots els objectes 2D, utilitzant les eines més adequades. Després feu les conversions necessàries a entitats 2D potencialment tridimensionalitzables -regions, polilínies. Opereu per tridimensionalitzar els objectes 2D -extrusió, revolució,etc. Modifiqueu els sòlids, si és necessari -xamfrà, empalmament, etc. Feu les operacions booleanes finals -unió, diferència, etc. 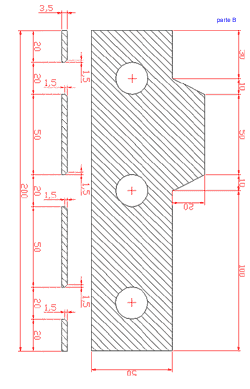Aquí teniu dues vistes en miniatura dels plànols amb les acotacions per fer l'exercici. Si hi feu clic a sobre, s'obriran dos documents HTML de dimensions òptimes per a la seva impressió.



	Un cop acabat l'exercici, guardeu-lo com a identificador de la xtec_m6_ex01.dwg. (Exemple: joanpuig_m6_ex01.dwg) Recordeu que heu de comprimir els document amb el WinZip i enviar-los al vostre tutor/a.