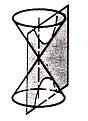Apol·loni va ser conegut com "El gran Geòmetra". El seu famós llibre "Seccions còniques", va introduir els termes: paràbola, el·lipse i hipèrbola espiral. Apol·loni de Perga va estudiar a Alexandria i després va visitar Pèrgam on havien estat construïdes  una biblioteca i una universitat semblants a la d'Alexandria.

Apol·loni, considera un sol con i fa variar la obliqüitat del pla que el talla. D'aquesta manera va obtenir com a corba fonamental la paràbola, la equació de la qual és y² = 2Px. Les altres dues corbes les caracteritza por : y²<2Px, que equival a la hipèrbola ("excés").

  En "Sobre el mirall que incendia" va mostrar que raigs de llum paral·lels no cauen a un focus a un mirall esfèric (com ha estat prèviament pensat) i va discutir les propietats focals d'un mirall parabòlic.

Va ser també un important fundador de l'astronomia matemàtica grega, la qual va fer servir models geomètrics per a explicar la teoria planetària.

Demostracions

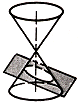
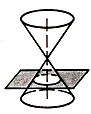
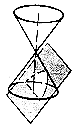
Còniques: en geometria, corbes formades per la intersecció d'un pla amb la superfície d'un con circular recte que s'estén cap a l'infinit a tots dos costats del vèrtex. La superfície del con a cadascun dels costat del vèrtex s’anomena "full" o "costat" del con. Donat un con en el que a es l'angle entre l'eix i la generatriu.

Si es talla el con amb un pla que forma un angle més gran que a amb l'eix, la intersecció és una corba tancada denominada el·lipse.
Si el pla és perpendicular a l’eix, la intersecció es una circumferència, que es considera com un cas particular d'el·lipse.
Si el pla talla a l’eix amb un angle igual a a , de manera que el pla és paral·lel a una generatriu del con, la intersecció es una corba oberta de longitud infinita anomenada paràbola.
Si el pla que talla el con es paral·lel a l’eix o forma un angle més petit que a, i sempre que el pla no contingui al vèrtex del con, la intersecció s’anomena hipèrbola. En aquest cas el pla talla als dos fulls del con i, per tant, la hipèrbola té dues branques que s’estenen fins a l’infinit

Las còniques són corbes planes o bidimensionals, per la qual cosa seria interessant el definir-les sense haver d’usar la noció de con, que és tridimensional. Una cònica acostuma a denotar-se fent servir la lletra e. Si P és un punt, Q es el punt de tall de la perpendicular de P a la directriu i F és el focus, el punt P  pertany a la cònica  si i només si (FP)=e(Q P), on (FP) i (QP) son les distàncies entre els respectius punts. Si e=1, la cònica és una paràbola; si e > 1, és una hipèrbola i si e<1, es una el·lipse.