Euler

§ Vida

Leonhard Euler va néixer a Basilea, Suïssa l’any 1707, i de ben petit ja demostrava senyals de genialitat. Va estudiar amb un dels famosos germans Bernoulli. Johann Bernoulli, que li feia de mestre i que en aquells temps era reconegut com un dels grans matemàtics del món. Euler es va graduar als 15 anys a la universitat. Quatre anys més tard va fer la seva primera aparició internacional, guanyant un premi de l’Acadèmia de les Ciències de París, per fer una impressionant anàlisi de la col·locació òptima dels pals ("mástiles") en un vaixell de passatgers (tot i que cal dir que ell mai havia vist un vaixell travessant un oceà). I

Al 1727 amb només vint anys viatjava a Rússia per ocupar lloc com a catedràtic a l’Acadèmia de Sant Petersburg on va residir fins que el 1741 va rebre una oferta millor de l’Acadèmia de Berlín, on s’instal·là durant més de vint-i-cinc anys.

Allí a Alemanya va mantenir contacte amb personatges tan famosos com D’Alembert, Manpertuis i Voltaire. Més tard, al 1766, retornà a Sant Petersburg fins a la seva mort al 1783 amb 76 anys, mentre que encara era un científic actiu.

La pèrdua gradual de la vista, a causa de l’excés de treball ,no va fer desaparèixer el seu caràcter simpàtic i humil ni tant sols cap a la fi de la seva vida on aquesta va esdevenir una ceguesa total.

Aquestes grans dificultats no van impedir les seves increïbles investigacions, doncs al contrari, la seva productivitat científica va augmentar. És gairebé increïble poder imaginar-se que mentre Euler esdevenia cec va fer uns avenços revolucionaris en el camp de l’òptica geomètrica. Euler va tenir una vida bastant dura i va haver de treballar molt per a poder mantenir a la seva nombrosa família formada per 13 fills i la seva dona.

En aquest breu text només comentaré uns pocs i petits exemples de la immensa producció d’Euler. Cal remarcar que el més valorat de la seva producció no és la quantitat dels seus treballs, que va ésser molta ,sinó la seva qualitat.

Euler va produir més de 900 treballs: llibres i escrits; publicant una mitjana de 800 pàgines de novetats científiques anuals, durant una vida activa d’uns 60 anys. Cap matemàtic en tota la història no ha estat capaç de pensar tant ràpidament, ni tant sols la majoria dels humans poden escriure a tanta velocitat .

A partir de 1911, un grup d’especialistes va començar a publicar les obres completes d’Euler amb el títol d’ Opera Omnia que no només conté treballs de matemàtiques sinó també problemes de mecànica, òptica, electricitat i acústica que va resoldre gairebé sempre amb la utilització d’una base matemàtica.

Al 1995 l’Opera Omnia estava formada per uns 70 volums (amb un gruix de 500 pàgines i un pes de 2kgs. cada volum) la meitat dels quals són aplicacions matemàtiques. Encara avui es creu que l’ Opera Omnia seguirà augmentant. Una de les coses més sorprenents d’Euler és que es va interessar per totes les branques de les matemàtiques. Pràcticament en totes les arts matemàtiques podem atribuir importants teoremes a Euler. No només va investigar i va fer grans avenços en la teoria dels nombres (aritmètica), càlcul (càlcul diferencial), àlgebra, probabilitats i geometria, també va explorar quasi en solitari noves branques de les matemàtiques com la teoria de les corbes, el càlcul de variacions i combinatòria. També va influir en la justificació dels nombres complexes i en definir la idea de funció. D’entre els seus textos, el més admirat és la “Introductio in Analysin Infinitorum” del 1748, que fins i tot ha estat comparat amb els “Elementos” d’Euclides.

Començaré parlant sobre la contribució d’Euler en la teoria dels nombres. Com ha pogut observar el matemàtic André Weil “ una parte sustancial del trabajo (sobre la teoría de los números) de Euler no consistió ni más ni menos sino en obtener demostraciones de las afirmaciones de Fermat…”

La teoria dels nombres d’Euler va omplir quatre grans volums de l’ Opera Omnia amb unes 1.700 pàgines de treballs teòrics. Es diu que encara que Euler no hagués fet cap altra cosa en la seva carrera científica, aquests quatre volums, el situarien entre els matemàtics més grans de la història.

Les investigacions d’Euler sobre la teoria dels nombres van ser afavorides pel fet que Euler no només se savia de memòria els 100 primers nombres primers, sinó que també se savia els seus quadrats, cubs i les seves quartes, cinquenes i sisenes potències. Podia dir en un moment i de memòria el resultat de (241)³ o de (337)⁶ .També era capaç de fer mentalment càlculs molt complexes, en els quals era necessari recordar fins a 50 xifres!!

A continuació explicaré una de les contribucions d’Euler a l’aritmètica superior. Aquest descobriment fa referència als nombres amigables o nombres amics. Aquest concepte apareix ja definit als temps de l’antiguitat. Els grecs varen definir els nombres amics com un parell de nombres on la suma dels divisors d’un, és igual a l’altre. Els nombres 220 i 284 són un clar exemple de nombres amics. Així: els divisors de 220 són 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110 i 220. Eliminant l’últim, obtenim que:

Durant segles, els matemàtics van haver de conformar-se amb aquest parell. El següent pas en aquest tema, va arribar al segle XIII, quan el matemàtic àrab ibn al-Banna, va descobrir el parell 17.296 i 18.416, aquest cop foren considerablement més complicats. Al 1636, el famós matemàtic francès Pierre de Fermat va redescobrir els nombres al-Banna i en va estar molt orgullós. Però al 1638, amb uns sentiments gens amigables, el seu etern rival matemàtic, també francès, René Descartes (1596-1650) va trobar un parell de nombres amigables encara més admirables, 9.363.584 i 9.437.056.

Com es diria avui en dia, Descartes “va deixar per terra” a Fermat, el va humiliar. El temps passava i el tema no progressava. Cal recordar que aleshores només es coneixien 3 parells de nombres amics: els dels grecs, al-Banna i Descartes. Doncs bé l’increïble Euler, després d’assabentar-se de l’existència d’aquests peculiars nombres, es va posar a treballar dur i va trobar més de 60 parells.

“Va deixar per terra a Descartes”. És evident suposar que el que va fer Euler va ésser trobar una manera, com un patró, que el va permetre de fabricar parells de nombres amics.

Hem vist abans que, els treballs d’Euler sobre la teoria dels nombres, consistien majoritàriament en demostracions de les afirmacions de Fermat. Doncs tot seguit en desenvoluparé un exemple.

En una carta de l’1 de desembre de 1729, Goldbach feia saber a Euler una famosa conjectura de Fermat, que deia que tots els nombres de la forma

+1 eren primers. Com es pot observar amb els 4 primers valors de n :

Encara no s’havia demostrat si era o no primer, però si no resultava ser-ho es desmentiria la conjetura de Fermat. Sens dubte qualsevol intent per a demostrar que la conjetura de Fermat era falsa calia un matemàtic capaç de descompondre el nombre 4.294.967.297 en dues parts. Euler es va concentrar i va trobar un descomposició del nombre:

El que no va fer Euler és posar-se a eliminar nombres que no fossin divisors de

+ 1, sinó que va fer una demostració molt enginyosa de perquè aquest nombre es podia descompondre. Aquesta demostració es pot trobar al llibre “Viaje a través de los genios” de William Dunham.

Igual que en la teoria dels nombres, Euler va fer grans avenços en geometria, inclosa la geometria elemental, que semblava que no donaria més sorpreses. Doncs Euler va saber omplir uns altres 4 grans volums amb més de 1.600 pàgines de la seva Opera Omnia.

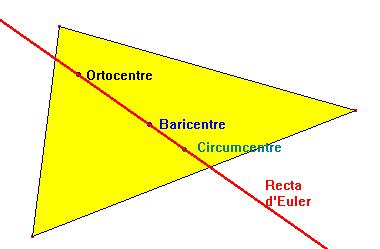
Euler va afirmar que en qualsevol triangle A,B,C hi ha una recta, (recta d’Euler) que passa a la vegada per l’ortocentre, el baricentre, el circumcentre i l’incentre. Euler va demostrar estar al mateix nivell que els antics Euclides, Arquímedes, Tales…

I del càlcul? Va contribuir Euler en el tema del càlcul diferencial i integral ? Doncs la pregunta té una resposta totalment afirmativa. Els seus textos sobre càlcul van ocupar gairebé 2.200 pàgines, ocupant del volum 10 al 13 de la seva Opera Omnia.

Com a exemple de la seva contribució en aquest tema podem trobar la suma d’una sèrie infinita específica que va ésser, sens dubte un dels seus primers grans èxits. Aquest problema va aparèixer al S.XVII, era un problema irresolt fins aleshores i consistia en calcular la sèrie de tipus:

que és la suma dels inversos dels quadrats de tots els nombres enters. Durant un temps, els matemàtics havien sabut que la suma de la sèrie donava una suma finita. Molts matemàtics importants, com els germans Bernoulli i Leibniz d’entre d’altres, van concentrar-se en el problema, però cap d’ells va saber treure cap conclusió. Euler va

fixar-se en aquest al 1734. Euler podia ja afegir-se a la llista dels matemàtics vençuts pel problema, quan va trobar una solució sorprenent .Va demostrar que la suma era igual a π²/6 . Aquest resultat va permetre de trobar d’una manera molt diferent a l’anterior un valor més aproximat de π.

Per acabar deixo al lector amb un segment del llibre “El universo de las matemáticas” de W.Dunham amb qui comparteixo totalment l’opinió. Això és tot.

“Los mismos que nunca han oído hablar de Euler probablemente no tendrían problema en saber que Pierre-Auguste Renoir es un artista o que Johannes Brahms es un compositor o que Sir Walter Scott es un novelista. La anonimidad de Euler, por contraste, es una injusticia y una vergüenza.

Pero lo que aún empeora el asunto es que los personajes comparables entre los pintores no son Renoir, sinó Rembrandt; entre los los músicos no es Brahms, sinó Bach; entre los escritores no es Walter Scott, sino William Shakespeare. Que un matemático comparable con semejantes personalidades – Euler es el Shakespeare de las matemáticas – atraiga un reconocimiento público tan pequeño es verdaderamente lastimoso.

Por tanto, encarezco a los lectores que blandiendo el libro comiencen a formar clubes de entusiastas seguidores, escriban pancartas y de otras muchas formas corran la voz acerca de uno de los matemáticos más influentes y más ingeniosos que han existido: el suizo Leonhard Euler”.