Las progresiones aritméticas y geométricas
Llamamos progresión aritmética a toda sucesión
real en la que cada uno de los términos (excepto el primero) se
obtienen del anterior sumando una constante que se denomina diferencia.
-
Ejemplo 1: La sucesión: 2, 4, 6, ... , 2n, ... es una progresión
aritmética creciente cuya diferencia es 2.
-
Ejemplo 2: La sucesión: 8, 7'5, 7, 6'5, 6, ... es una progresión
aritmética decreciente de diferencia -0'5.
Una progresión geométrica es creciente cuando la diferencia
es positiva y decreciente cuando es negativa.
Llamamos progresión geométrica a toda sucesión
real en la que cada uno de los términos (excepto el primero) se
obtiene del anterior multiplicandolo por una constante que se denomina
razón de la progresión.
-
Ejemplo 1: La sucesión: 1, 2, 4, 8, ... , 2n, ... es
una progresión geométrica creciente cuya razón es
2.
-
Ejemplo 2: La sucesión: 2, -2, 2, -2, 2, ... es una progresión
geométrica oscilante de razón -1.
-
Ejemplo 2: La sucesión: 4, 2, 1/2, 1/4, ... es una progresión
geométrica decreciente de razón 1/2.
La razón y el primer término nos determinan el carácter
de la progresión.
| Raón/1r término |
Positivo |
Negativo |
| >1 |
Creciente |
Decreciente |
| entre 0 y 1 |
Decreciente |
Creciente |
| <0 |
Oscilante |
Oscilante |
Un ejemplo de progresión geométrica es la sucesión
de les frecuencias de las notas en la escala
temperada. Es una progresión geométrica de razón 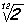
|
