Funcions estadístiques d'Excel
7. Simulacions i ajust
Simulacions
Per a generar sèries uniformes de nombres aleatoris cal prendre en el menú Herramientas l'opció Análisis de datos i en ell triar Generación de números aleatorios.
Ara s'han de fixar:
Número de variables
Cantidad de números aleatorios: nombre
de vegades que es repeteix l'experiència simulada.
Distribución: Uniforme
Parámetros: si a i b són els
valors extrems enters que es volen obtenir, cal posar entre a i b+1.
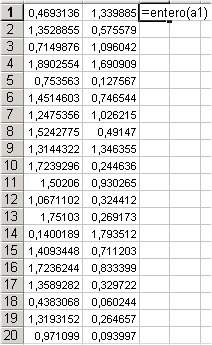
Si es vol que els resultats siguin enters cal transformarlos per mitjà de la funció ENTERO( ).
En l'exemple següent es tiren dues monedes
20 vegades.
 |
 |
 |
 |
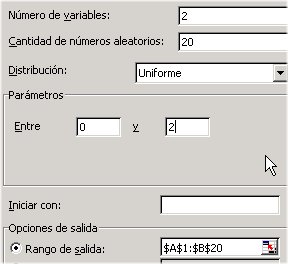
| variables: 2 perquè hi ha
dues monedes
cantidad: 20 perquè es tiren 20 vegades distribución: uniforme perquè tant pot sortir cara com creu entre 0 i 2: perquè hi ha dues possibilitats, cara o creu |
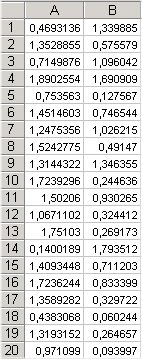
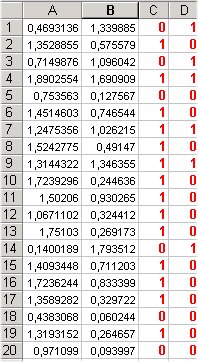
aquest és el resultat:surten nombres decimals entre 0 i 2 | la fórmula entero() els transforma en enters 0 i 1 | aquest és el resultat: els 1 poden significar cares i els 0 creus |
Per a generar sèries de nombres aleatoris seguint una distribució discreta prefixada:
En primer lloc cal preparar en un full una taula
amb els possibles valors i les seves probabilitats; aquestes han de sumar
1.
A continuació cal prendre en el menú
Herramientas
l'opció Análisis de datos i en ell triar Generación
de números aleatorios.
Ara s'han de fixar:
Número de variables: per exemple 4
si es volen simular les tirades de 4 monedes.
Cantidad de números aleatorios: nombre
de vegades que es repeteix l'experiència simulada.
Distribución: Discreta
Rango de entrada de valores y probabilidades:
indicar la taula que s'ha preparat abans.
En l'exemple següent es tira 60 cops un dau
trucat en què els nombres senars tenen probabilitat 1/4 i els nombres
parells probabilitat 1/12
 |
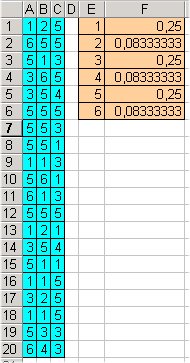 |
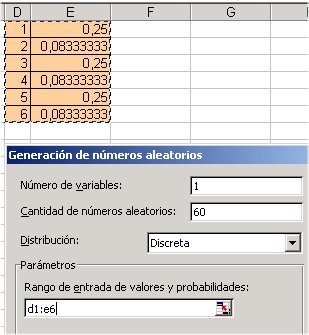
| S'introdueix la taula de resultats
possibles 1, 2, 3, 4, 5, 6 i les seves probabilitats (1/4 = 0,25, 1/12
= 0,8333...)
Una variable (un sol dau) Cantidad 60 (60 tirades) Distribución discreta Rango: la posició de la taula de valors |
|
Ajust a un model
Si A1:An són les freqüències reals i B1:Bn les freqüències teòriques es fa PRUEBA.CHI(A1:An;B1:Bn) i s'obté el risc d'equivocació en rebutjar l'ajust.
Per exemple per comprovar si les tirades del dau
anterior s'ajusten a allò previst:
 |
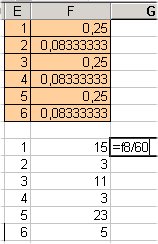 |
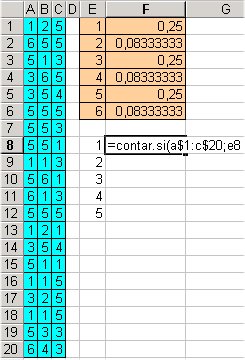
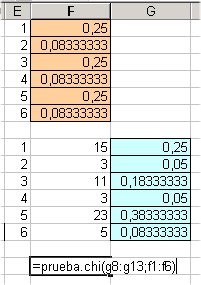 |
| En primer lloc es fa el recompte de les freqüències de cada resultat | A continuació es calculen les freqüències relatives, dividint pel total de tirades | Les freqüències reals (fons verd) es comparen amb les esperades (fons taronja). El resultat és 0,9997. El risc d'equivocar-nos al dir que el dau no està d'acord amb el previst és del 99,97% |