Molt bé, molt bé, no hem avançat gaire. El llibre no és una novel·la, però té parts de ficció. No és un manual, però té parts prou pedagògiques. No és un assaig, però té també parts de discurs assagístic. Així doncs, què és? Doncs un llibre, com us deia abans.

Intentem-ho d'una altra manera: si no tenim clar què és, fixem almenys de què s'ocupa. El llibre parla de música (i de Johann Sebastian Bach en particular); però no és un llibre de música. El llibre parla d'art (i dels dibuixos de M. Cornelis Escher en particular); però no és un llibre d'art. El llibre parla de matemàtiques (i del teorema d'incompletesa de les matemàtiques demostrat per Kurt Gödel en particular); però no és un llibre de matemàtiques. Així doncs, de què va el llibre?

Ara ja de debò: Gödel, Escher y Bach és un llibre desbordant. Si hagués de descriure en poques paraules quin és el contingut del llibre, diria que tracta de si un sistema pot comprendre's a si mateix. Dit d'una altra manera, de si hi ha sistemes que surten de si mateixos. Ho il·lustraré amb dos exemples dels molts que apareixen en el llibre: un dibuix d'Escher i una partitura de Bach.

Fixeu-vos en el següent dibuix d'Escher:

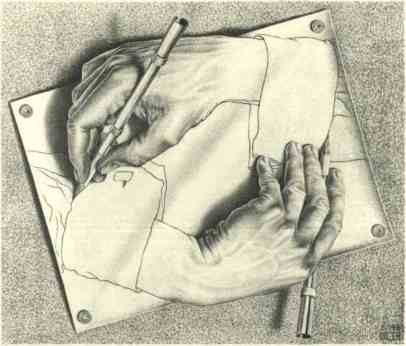
Hi ha una mà que dibuixa una altra mà la qual, al seu torn, ¡dibuixa la primera mà! Què és real i què és dibuixat? Hi ha dos nivells diferents dins el dibuix? D'acord, potser sí, acceptem que hi ha dos nivells; però aleshores, quin és el primer nivell?, quin nivell depèn de quin altre?

El dibuix es tracta d'un dibuix que surt de si mateix (un sistema que surt de si mateix). Molts altres dibuixos d'Escher (en trobareu a http://www.mcescher.com/ (i a moltes altres pàgines)) plantegen problemes similars.

Observeu ara la següent partitura de Bach:

Es tracta d'un cànon. Els qui sabeu música (o sigui tots, perquè tots n'heu estudiat a l'institut) podeu provar a cantar-lo amb algú altre, cadascú una veu. Sona bé, oi? Observeu ara el següent: ¡la segona veu és exactament la mateixa que la primera veu, només que en sentit invers! ¿És la simetria del Cànon Invers una prova d'un altre sistema establert a dos nivells?

Finalment, menciono només a Gödel -tot i que constitueix el gruix del llibre. Simplificant molt les coses, Gödel mostra com no tots els teoremes de les matemàtiques són demostrables des de les matemàtiques. En conseqüència, resulta que les matemàtiques són un sistema incomplet.

Bé, doncs el llibre parla d'aquestes coses, i les relaciona també amb altres camps d'estudi de la ciència. El llibre és dens, sí, però amè al mateix temps. I demana esforç i interès per llegir-lo, però a hores d'ara, si heu arribat a segon de batxillerat, hauríeu d'haver après que, en general, les coses que requereixen un esforç acostumen a resultar després terriblement profitoses.

Probablement no es tracta d'un llibre que pugueu llegir de manera lineal i d'una sola tirada; però és un llibre del qual, almenys els qui tingueu interès per qüestionar-vos els límits del coneixement, està bé que conegueu la seva existència. L'estructura del llibre és, d'altra banda, força atractiva i també curiosa: en general els problemes són introduïts per un diàleg entre Aquil·les, el veloç corredor grec, i la tortuga que el repta a una cursa en les clàssiques paradoxes de Zenó que heu estudiat a les classes de filosofia. El diàleg aconsegueix presentar de manera planera les qüestions que es debatran tot seguit en cada capítol.

Deia que problement no és un llibre que sigui fàcil de llegir d'una sola tirada. Afegeixo que probablement no es tracta tampoc d'un llibre que us hagi d'interessar a tots. Però estic convençut que si alguns li doneu un cop d'ull, segur que no us en penedireu.