Introducció a la hidrodinàmica

  Règims de corrent

 El tipus de règim depèn de la velocitat a la qual circula el líquid i de les irregularitats i obstacles que troba en el seu camí.

 Així un flux pot ser: · Laminar (ordenat i uniforme)

                                 · Turbulent ( desordenat i amb turbulències)

                                      Flux laminar                                                          Flux turbulent

 Flux laminar: Les diferents partícules del fluid es mouen en trajectòries paral·leles i formen làmines.

 Flux estacionari: En un determinat punt de la massa fluida, la velocitat de les diferents partícules que hi passen sempre és la mateixa.

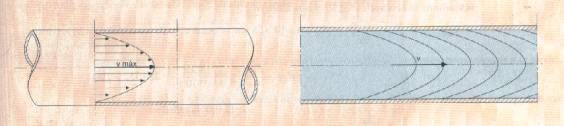
 Tot si que la velocitat en un flux pot variar, a efectes de càlcul es considera una única velocitat considerada com la mitjana de les diferents velocitats de cada làmina i que es situa a l’eix central de la canonada.

Nombre de Reynolds

Per determinar si en una canonada el flux és laminar o turbulent s’utilitza el nombre de Reynolds. És un nombre adimensional donat pel quocient entre les forces d’inèrcia ( F_i = m a ) que tendeixen a provocar turbulència i les forces degudes a la viscositat ( F_m  ) que les esmorteeixen.

R_e =   F_{i  /}  F_m

 El nombre de Reynolds per a canonades circulars val:

R_e = v d r             R_e = v d

m                                                        u

 v = velocitat mitjana en m/s

d = diàmetre de la canonada en m

r = densitat del fluid en Kg/m³

m = viscositat absoluta en Pa·s o N·s/m²

u = viscositat cinemàtica del fluid en m²/s 

Si el valor és inferior a 2000 el règim és laminar. 

Cabals màssics i volumètrics 

Cabal: Quantitat de fluid que travessa una secció donada per unitat de temps. Es pot expressar en massa ( cabal màssic ) o en volum ( cabal volumètric ).

 Aquests dos tipus de cabal es relacionen per la densitat del fluid. La densitat és la massa per unitat de volum: r = m/V.

 El cabal màssic en el SI s’expressa en Kg/s i el volumètric en m³/s. En la pràctica es fa servir el L/s, L/min o el m³/h.

Equació de continuïtat 

Quan es tracta de líquids incompressibles i amb flux laminar i estacionari, el cabal volumètric de líquid que passarà per cada tram d’una conducció amb diferents seccions, serà constant.

 Q₁ = Q₂ = Q₃ = Q_n

Q₁ = V₁ = A₁ L₁ = A₁ v₁

Q = cabal volumètric

V = volum de líquid d’un tram de conducció

A = àrea d’una secció transversal de canonada

L = longitud del tram

 v = velocitat mitjana normal a la secció considerada

Com que els cabals que travessen cada secció són iguals, sempre que no hi hagi llocs on es perdi líquid, l’anterior equació es transforma en l’equació de continuïtat:

Q = A₁ v₁ = A₂ v₂ = A_n v_n = constant

D’aquesta es dedueix que les velocitats són inversament proporcionals a la secció de cada tram.

Com que la majoria de conduccions són se secció circular, l’anterior equació es pot transformar en la següent:

Q = p D²₁  v₁ = p D²₂  v₂                        D²₁  v₁ = D²₂   v₂

                              4               4

Aquí es dedueix que la velocitat varia inversament al quadrat del diàmetre.

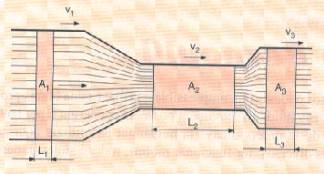
                           Canonada amb diferents seccions. Llei de continuïtat.

Transferència d’energies en un fluid. Teorema de Bernoulli

 L’energia que posseeixen els fluids en moviment es manifesta en forma de: energia potencial gravitatòria, energia de pressió i energia cinètica.

Energia potencial gravitatòria 

L’energia potencial gravitatòria fa referència a l’energia que posseeix la massa d’un fluid deguda a la seva elevació respecte una cota de referència.

 E_p = m g h

Energia de pressió

L’energia de pressió és una energia hidrostàtica deguda a la pressió del fluid capaç de realitzar un treball.

 W = p A x = p V  ( J ) 

p = pressió en Pa

A = superfície en m²

x = distància en m

V = volum en m³ 

Energia de pressió: E_pr = p V = p A x

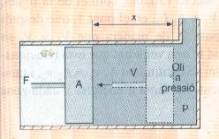
                                                               Dibuix d’un cilindre seccionat.

Energia cinètica  

L’energia cinètica és l’energia que te el fluid deguda a la seva velocitat.

 Energia cinètica = E_c = m v² / 2

 L’energia total del fluid és la suma de les tres energies: 

Energia total: E_T = E_p + E_pr + E_c = m g h + p V + 1 m v² / 2

Ja que la massa és el producte de la densitat pel volum (m = r V ) l’equació anterior es transforma en:

 E_T = r g h + p + 1 r v² / 2

En mecànica de fluids de vegades s’utilitza l’energia com a quantitat d’energia per unitat de pes del fluid. Si dividim l’expressió anterior pel pes específic g s’obté:

H = h + p + v²

             rg   2g

h = cota topogràfica

p   = altura de pressió

rg

v²     = altura de velocitat

2g   

 Suposem un tub de secció variable i considerem dins d’ell un volum V₁ = A₁ L₁, en el punt 1, que després d’un cert temps es desplaça al punt 2, de manera que V₁ = V₂   i   A₁ L₁ = A₂ L₂. A cada punt el fluid té una velocitat que està relacionada amb la secció, d’acord amb la llei de continuïtat A₁ v₁ = A₂ v₂, i també una pressió p₁ i p₂ respectivament. La suma d’energies a cada zona serà equivalent:

m g h₁ + p₁ V₁ + 1 m v²₁ = m g h₂ + p₂ V₂ + 1 m v²₂

2                                                                                         2

 Si dividim l’expressió anterior entre el volum, tot considerant que la massa és el producte de la densitat pel volum, ens queda:

r g h₁ + p₁ + 1 r v²₁ = p₂ + 1 r v²₂

2                                          2

Expressió coneguda com a teorema de Bernoulli o teorema fonamental de la hidrodinàmica, per a un fluid ideal.

L’equació de Bernoulli, deduïda per a dues seccions arbitràries dins d’un mateix tub de corrent, es compleix per a qualsevol secció del tub de corrent. Ës per això que podem rescriure-la així:

r g h + p + 1 r v² = constant

                                                            2

Si la conducció és horitzontal, h₁ = h₂, l’energia potencial gravitatòria serà igual en els dos punts considerats i per això no caldrà considerar-la:

p₁ + 1 r v²₁ = p₂ + 1 r v²₂

2                                             2

Expressió que mostra que si augmenta la velocitat del fluid, la pressió disminuirà per poder mantenir l’equilibri energètic.

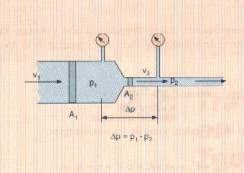
Experimentalment pot observar-se aquest efecte col·locant dos manòmetres en dues zones d’una canonada de secció no uniforme, de manera que el manòmetre que es troba en la zona de menor secció marcarà menys pressió, ja que d’acord amb la llei de continuïtat v₂ = A₁ v₁ / A₂, la seva velocitat serà major que a la zona de secció més gran. Aquest fenomen pot utilitzar-se per conèixer la velocitat del fluid que circula per la part principal de la canonada:

p₁ – p₂ = 1  D  A²₁ – A²₂   v²₁

   2          A²₂

d’on es dedueix que:

                                         1/2

v₁ = A₂  2 ( p₁ – p₂ )

       D ( A²₁ – A²₂ )

Una aplicació d’aquest principi és el polvoritzador. En prémer la bola de la goma, s’impulsa aire a través d’un petit estrenyiment. En ser la pressió en aquest punt inferior a l’atmosfèrica es crea una petita depressió que fa que el líquid del recipient pugi pel tub vertical fins al raig d’aire, on es polvoritza.

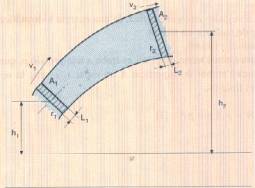
Teorema de Bernoulli.                                          Canonada de secció no uniforme amb dos               manòmetres.

Potències

¨ Potència hidràulica:   

P = p · V / t =  p Q     [watt]

Si la pressió la donem en metres de la columna de líquid: P = Q (r g h)

¨ Potència consumida:  Pc = p Q/ h = Q(r g h / h) [watt]

¨  Pèrduda de càrrega : és la disminució de pressió que experimenta un líquid en circular per un conducte. Hi ha dos tipus:

• Pèrdudes primàries
• Pèrdudes secundàries

H_pc = h_p + h_s

-         h_pc: energia perduda

-         h_p: pèrdudes primàries

-         h_s: pèrdudes secundaries

expressada en altures equivalent:

h₁ + p₁ / r g + v₁² / 2 g – h_pc = h₂ + p₂ / r g + v₂² / 2 g

Si la canonada es horitzontal h₁ = h₂ i de secció constant v₁ = v_2:

p₁ – p₂ / r g = h_pc

¨  Equació de Boyle-Mariotte:  p₁ V₁=p₂ V₂=p₃ V₃ = constant

p= pressió    V= volum

¨ Llei de Gay-Lussac o Llei de Charles: 

V₁/T₁=V₂/T₂=V₃/T₃       p₁/T₁=p₂/T₂=p₃/T₃         p₁ V₁/T₁=p₂ V₂/T₂=p₃ V₃/T₃    

V=volum       T=temperatura

¨ Equació d’estat dels gasos perfectes:  

p₁ V₁/T₁=p₂ V₂/T₂=p₃ V₃/T₃ = constant = K

es dedueix que: P V= K T

K  es una cosntant que per a n mols d’un gas ideal val: K = nR

R és constant universal dels gasos ideals = 8,314 J/K · mol

P V =  n R T

¨ Processos termodinàmics:

- Processos isobàrics: Procés termodinamic on la presio es constant

F= p A

Treball realitzat:   W = F Dx = p A Dx = p DV = p (V₂ – V₁)   [Joules]

- Processos isotèrmics: El que té lloc a temperatura constant

pV=K

W=n R T ln (V₁/V₂)

¨ Energia potencial:   W=Ep=pV  [Joules]

¨ Pontència:  P=pQ=pV/t=pAv  [watt]       

Q= cabal          p=pressió      V=volum       A=superfície del èmbol       v=velocitat

 Exercicis

1. Esbrina el règim que s’estableix en una canonada de 177 cm² de secció per la qual circula un oli de densitat relativa 0,9 i viscositat absoluta de 3,15 poise, a una velocitat de 2 m/s.

2. Què entenem per cabal? En què es diferencien el cabal màssic i el cabal volumètric? Quina és la magnitud que els relaciona?

Solucions

1.                    R_e = v d r                        177 cm² = 0,0177 m²

                       m                           0,0177 = p r²         r = 0,075          d= 0,15 m

                                                    r = 0,9 · 1000          r = 900

3,15 poise   1 Pa/s   = 0,315 Pa/s

                  10 poise

R_e = 2 · 0,15 · 900 = 857,14  < 2000      Règim laminar.

             0,315

2.  El cabal és la quantitat de fluid que travessa una secció per unitat de temps. El cabal màssic s’expressa en massa i el volumètric en volum i estan relacionats per la densitat del fluid.

¨ Sistema hidràulic de dos dipòsits intercomunicats amb una bomba que fa transvassament d’un líquid ( r=0,9 kg/dm³ ) del depòsit 1 al depòsit 2. En un instant  l’alçàries del fluid, respecte el plànol de referència: h1=2m h2=6m. Cabal= 0,13 m/s.Diàmetre canonada=55mm. Calcula: Pressió q ha de generar la bomba, la potència i la velocitat de sortida del fluid.

Pressió    Ap=p2-p1=(r g h2)-( r g h1)=pg(h2-h1)=900 · 9,8(6-2)=35280 Pa

Potència     P=pr Q= 35280 · 0,13= 4586,4 w

Velocitat   Q= A v Þ V=Q/A = 0,13/0,475=0,27 m/s

                        A=p·d²/2=3,14·(0,055)²/2=0,475m²

¨ Un recipient de 4000L conté aire a una pressió de 7 bar i temperatura constant. Determina l’augment de pressió experimentat pel fluid si reduïm el volum un 31%.

P1 V1=p2 V2 Þ 7·4000=p2· 1240 Þ p2=28000/1240= 22,5 bars

V2 = 4000 · 31/100= 1240

Ap= p2-p1= 22,5 – 7 = 15,5 bar