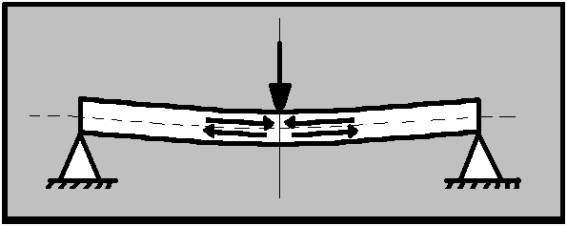
L’Esforç de Flexió
Definició: Quan una barra és sotmesa a l’acció de forces que tendèixen a doblegar-la diem que esta sufrin un esforç de flexió.
Els esforços de flexó són una compocicó dels esforços de tracció i de compresió.
Tracció: Un obgecte sufreix un esforç de tració quan esta sotmes a dues forces d’igual modul i direcció, peró amb sentit contrari i orientades cap a fora i sempre perpendicular a la secció.
Compressió:
Un
obgectesufrei un esforç de compressió quan esta sotmes a dues forces d’igual
modul i direcció, peró amb sentit conrari i orientades
cap a dins
i sempre pependicular a la secció.

1.-
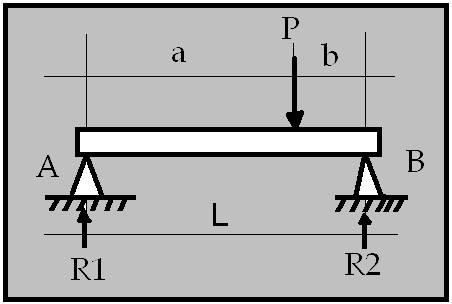
El dibuix representa una biga
recolzada en els seus dos extrems i amb una força puntual (que
podrien ser mès) i per tan les reaccions en els seus dos extems són oposades a
la força P .
Equació
per calcular les resultants (R):
R1=R2=P/2
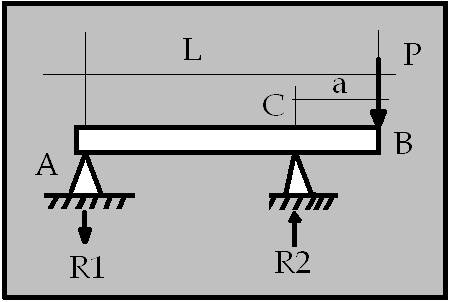
2.-
El
dibuix representa una biga
recolzada amb volandis i càrrega puntual i per tant la
reacció en el suport C és contraria a la força P,
però la reacció A és igual que la força P perque
sino fos així la biga s’aixecaria .
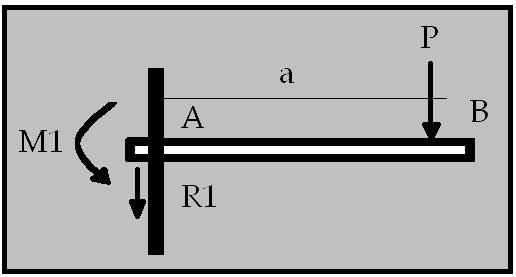
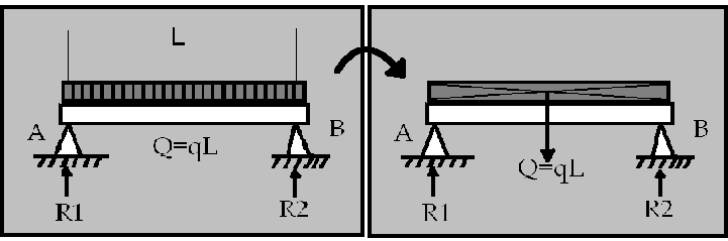
- Tot seguit us mostrem una taula on es troben els tipus d’ esquema caracteristic de cada tipus de biga. El prime dibuix de cada quadre representa el tipus de biga, el segon és la grafica de les forces tallants i el tercer equibal al grafic de moments flexsors.
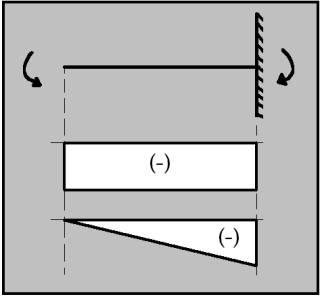
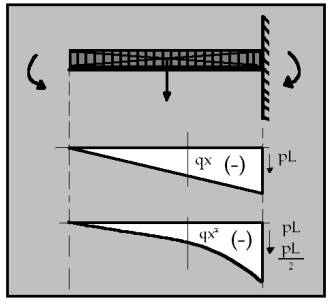
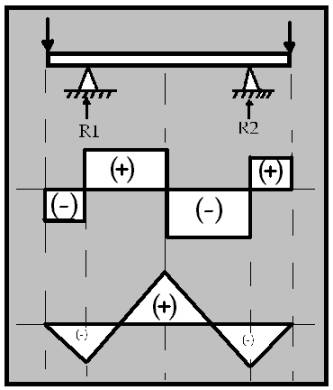
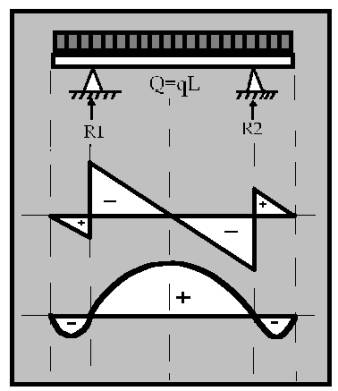
Exercicis
1.- Fes els diagrames dels moents flexors i de les forces tallants i determina el moment flexor maxim en cadascun dels següents casos:
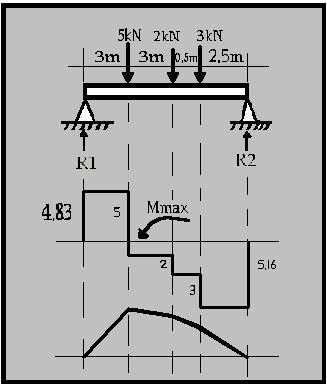
Em=0
Emy=0
A
R1 0 - 3 5 - 6 2 - 6.5 3 + 9R2 = 0 ;
0-15 - 12 - 19.5 + 9R2 = 0; -6.5 + 9R2 = 0
9R2 = 6.5 ----------------
R2 = 46.5 / 9
R2
= 5166.6N
B R2 0 - 2.53 3 – 3 2 –6 5 + 9R1 = 0; 0 – 7.5 – 6 – 30 + 9R1 =0; -43.5 + 9R1 = 0
9R1 = 43.5
------------------ R1 = 43.5 / 9
R1
= 4833.3N
Mmax = 3R1
Mmax = 14.49KN
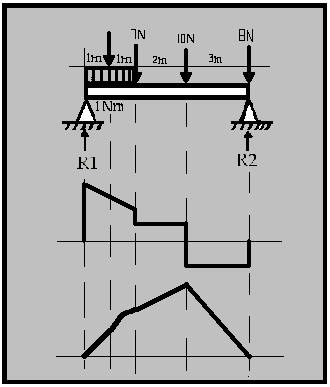
Em = 0
Emy = 0
A R1 0 –2 1 – 7 2 - 10 4 – 8 7 + 7R2 = 0
0 – 2 –7 –40 – 56 + 7R2 = 0
-105 + 7R2 = 0
R2 = 150 / 7 ----------------------- R2 = 16N
B
R2 0 – 8 0 – 10 3 –7 5 – 2 6 + 7R1 = 0
0 – 0 –30 – 42 – 12 + 7R1 = 0
7R1 – 84 = 0
R1 = 84 / 7 ----------------------- R1 =11N
Mmax = 3R2 – 8 3
Mmax
= 6 3 – 8 3 ----------------- Mmax = 24