|
No et deixis enganyar
A continuació es descriuen cinc situacions on apareixen, directament o indirectament, els temes de mitjanes i dispersions. Analitza-les críticament.
- "Jo sóc el millor perquè tinc més bones notes que la mitjana de la classe."
- "Aquest producte no engreixa perquè té un 20% menys de greix que la mitjana dels altres productes del mateix tipus."
- "Si la desviació típica és zero, és que tots els resultats són iguals."
- "Com que la fondària mitjana del riu és d'1 metre, no hi ha perill d'ofegar-se."
- "Si pogués triar professor/a de matemàtiques, aniria a la classe en què la mitjana de notes fos més alta."
Recorda
Mesurar la dispersió és veure com estan d'allunyats els resultats a1, a2,..., an de la seva mitjana aritmètica: M= (a1+a2+a3+a4+a5)/n. Una mesura de dispersió és la desviació típica que es calcula amb la fórmula següent:
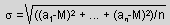
|
Problemes
- En un barri hi ha un mateix producte detergent que es ven a cinc preus diferents: 200, 250, 225, 199 i 219 pessetes. Calcula la mitjana del preu i la desviació típica. Es pot dir que hi ha enormes diferències de preu?
- Un cop analitzats els salaris d'un ofici en una comarca, s'ha vist que la mitjana del salari és de 60.000 pessetes i la desviació d'unes 40.000 pessetes. Què en pots concloure?
- Un producte que valia 100 pessetes al gener ha augmentat 10 pessetes cada mes al llarg de l'any. Calcula la mitjana del preu i la desviació.
Més coses
- Quina desviació típica hi ha en les alçades dels alumnes de la teva classe?
- Busca un conjunt de nombres la mitjana dels quals sigui 0 i la desviació típica sigui 5. Fes-ne interpretacions.
|