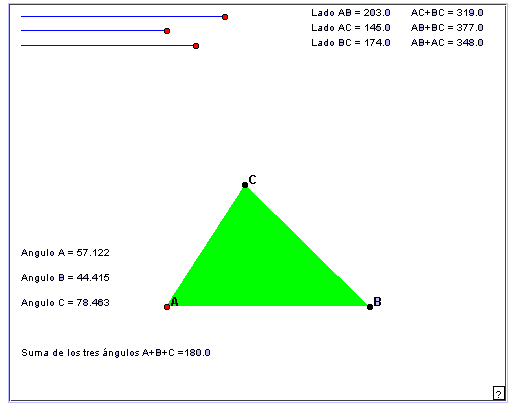
Geometría Animada e interactiva : Construyendo un triángulo con tres segmentos.

Objectivos
Al acabar la ficha de trajo el alumno/a de ser capaz de :
1. Construir un triángulo, si es posible, dados tres segmentos.
2. Medir la longitud de un segmento y hacerla aparecer en algún lugar del Applet.
3. Medir la amplitud de un ángulo y hacerla aparecer en algún lugar del Applet.
4. Operar con longitudes de segmentos y medidas de ángulos y escribirlas en el Applet.

Instruciones
1. Cliquee y arrastre los puntos rojos.
2. Cliquee sobre los botones que hay dentro del applet para hacer que los objetos se muevan o que nuevos objetos aparezcan o desaparezcan.
3. Cuando los objetos son de animación o movimiento, pulsar tecla > para acelerar el movimiento o la tecla < para frenar.
4. Presione R para reajustar el applet a su configuración inicial.
5. Pulsar el X rojo de la esquina inferior derecha para eliminar la traza u objetos nuevos.

Reglas particulares del ejemplo 1
1. Experimenta variando los lados del triángulo, arrastrando los puntos rojos.
2. Observa las longitudes de los lados cuando el triángulo desaparece y contesta a la pregunta. ¿Cuándo no se puede construir el triángulo?
3. El triángulo se puede arrastrar a partir del punto A
4. Trata de deducir los pasos para construir el triángulo.
5. Observa la medida de los tres ángulos y de los lados que tienen en frente.

Volver al principio de la página

Lee y recuerda

Para dibujar un triángulo, a partir de tres segmentos dados, se hacen los pasos siguientes:

Se dibuja el primer segmento AB

Se dibuja la circunferencia de centro A y radio el segundo segmento AC.

Se dibuja la circunferencia de centro B y radio el tercer segmento BC.

Se busca uno de los puntos de intersección C de las dos circunferencias anteriores. Este punto es el tercer vértice del triángulo.

La suma de dos lados del triángulo siempre es mayor que el lado restante.

La suma de los ángulos de un triángulo siempre es un ángulo llano (180 grados).

Volver al principio de la página

Lee y practica

Observa el dibujo de la derecha. Es la figura que se construye con el siguiente programa. Los tres segmentos de la parte superior se pueden alargar y acortar dando lugar a que el triángulo cambie de forma o incluso que no se pueda construir. Copia el texto y guarda el fichero con el nombre jsp04.HTM

<HTML><HEAD> <TITLE> Geometría animada 4 </TITLE> </HEAD> <BODY> <CENTER> <h2>IES JOAN D'ÀUSTRIA</H2>

<H6>Profesor: Antonio Hernández Gómez</H6>

<H5>Alumno: </h5>

<APPLET CODE="GSP.class" CODEBASE="."

WIDTH=500 HEIGHT=400

Archive="JSPDR3.JAR">

<PARAM NAME=MeasureInDegrees value=1>

<PARAM NAME=Construction VALUE="

{1} Point(10,10)[hidden];

{2} Point(10,300)[hidden];

{3} Line(1,2)[hidden];

{4} Perpendicular(3,1)[hidden];

{5} Perpendicular(3,2)[hidden];

{6} Point on object(3,0.9)[hidden];

{7} Point on object(3,0.95)[hidden];

{8} Perpendicular(3,6)[hidden];

{9} Perpendicular(3,7)[hidden];

{10} Point on object(4,1.2);

{11} Point on object(9,1.0);

{12} Point on object(8,1.1);

{13} Point on object(5,1.0)[label('A')]; {punto A}

{14} Segment(1,10); {Segmento AB}

{15} Segment(7,11); {Segment AC}

{16} Segment(6,12); {Segmento BC}

{17} Length(14, 300,10, 'Lado AB = ');

{18} Length(15, 300,25, 'Lado AC = ');

{19} Length(16,300, 40, 'Lado BC = ');

{20} Circle by radius(13,14) [hidden];

{Circunferencia de centro A y radio AB}

{21} Intersect2(5,20)[label('B')]; {Punto B}

{22} Circle by radius(13,15)[hidden];

{Circunferencia(A,AC)}

{23} Circle by radius(21,16)[hidden];

{Circunferencia(B,BC)}

{24} Intersect1(22,23)[label('C')];

{25} Polygon(13,21,24)[green];

{26} Angle(21,13,24,10,250, 'Angulo A = ');

{27} Angle(24,21,13,10,275, 'Angulo B = ');

{28} Angle(13,24,21,10,300, 'Angulo C = ');

{29} Calculate(400, 10, 'AC+BC = ', 'AB+')(18,19);

{30} Calculate(400, 25, 'AB+BC = ', 'AB+')(17,19);

{31} Calculate(400, 40, 'AB+AC = ', 'AB+')(17,18);

{32} Calculate(10,350, ‘A+B+C =', 'AB+C+')(26,27,28);

"> </APPLET>

<h2>Dibujo de un triangulo dados los tres lados</h2>

</CENTER> </BODY> </HTML>

¿ Qué medidas han de tener los segmentos para que no puedan formar triángulo?
(2puntos)

Añadir una instrucción que verifique que el ángulo 180-B es siempre mayor que el ángulo A. (2 puntos)

Volver al principio de la página

Código fuente suministrado al applet jsp4·JAR


{ Puntos y recta auxiliar  para trazar los segmentos que seran los lados }
  {1} Point(10,10)[hidden];
  {2} Point(10,300)[hidden];
  {3} Line(1,2)[hidden];   
 
{Rectas auxiliares que contendrán las direcciones de los segmentos-lados} 
  {4} Perpendicular(3,1)[hidden];
  {5} Perpendicular(3,2)[hidden];
  {6} Point on object(3,0.9)[hidden];
  {7} Point on object(3,0.95)[hidden];
  {8} Perpendicular(3,6)[hidden];
  {9} Perpendicular(3,7)[hidden];
  {10} Point on object(4,1.2);
  {11} Point on object(9,1.0);
  {12} Point on object(8,1.1);
  {13} Point on object(5,1.0)[label('A')]; {punto A}

{Trazado de los segmentos que seran los lados
  {14} Segment(1,10); {Segmento  AB}
  {15} Segment(7,11); {Segment AC}
  {16} Segment(6,12); {Segmento BC}

{Cálculo y escritura de la longitud de los segmentos-lado} 
 {17} Length(14, 300,10, 'Lado AB = '); 
  {18} Length(15, 300,25, 'Lado AC = ');
  {19} Length(16,300, 40, 'Lado BC = ');

{Dibujo del triángulo}
  {20} Circle by radius(13,14)[hidden];{Circunferencia de centro A y radio AB}
  {21} Intersect2(5,20)[label('B')]; {Punto B}
  {22} Circle by radius(13,15)[hidden]; {Circunferencia(A,AC)}
  {23} Circle by radius(21,16)[hidden]; {Circunferencia(B,BC)}
  {24} Intersect1(22,23)[label('C')];
  {25} Polygon(13,21,24)[green];

{Cálculo y escritura de la medida de los ángulos}
  {26} Angle(21,13,24,10,250, 'Angulo A = ');
  {27} Angle(24,21,13,10,275, 'Angulo B = ');
  {28} Angle(13,24,21,10,300, 'Angulo C = ');

{Calculo y escritura de la suma de las longitudes de los pares de lados}
  {29} Calculate(400, 10, 'AC+BC = ', 'AB+')(18,19); 
  {30} Calculate(400, 25, 'AB+BC = ', 'AB+')(17,19);
  {31} Calculate(400, 40, 'AB+AC = ', 'AB+')(17,18);

{Cálculo y escritura de la suma de los tres ángulos}
 {32} Calculate(10,350, 'Suma de los tres ángulos A+B+C =', 'AB+C+')(26,27,28);

Volver al principio de la página

Introducir las ordenes del ejemplo que deseéis construir:

Volver al principio de la página