LOS FASCINANTES CUADRADOS MÁGICOS

     Comenzamos a conocerlos desde jóvenes, un buen día llega algún amigo o conocido con ganas de hacernos reflexionar un poco o de dejarnos en evidencia y nos propone resolver, mientras dibuja un cuadrado dividido en tres partes horizontales y verticales, lo siguiente:
     ”A ver si eres capaz de situar los números del 1 al 9 en esta tabla de 3 por 3 casillas de manera que todas las filas, columnas y diagonales sumen 15”
como si esto fuese la última novedad en pasatiempos... (¡¡Pobre infeliz!!)
    Y tú que, quizás, desconocías el “problemita” vas y rompes la cabeza un buen rato hasta comprender que el número 5 ha de ir en el centro del cuadrado y entonces, sin demasiadas dificultades, se llega a una de las muchas soluciones posibles. Supongo que la mayoría de nosotros hemos acabado saliendo airosos de esta experiencia, que más o menos ocurrió de este modo...
    En mi caso recuerdo que cuando ví la solución y me enteré que los llamaban “cuadrados mágicos”, me provocó, desde el primer momento, una gran curiosidad. Así que no tuve suficiente y busqué, dedicando una buena cantidad de tiempo, resolver el “cuadrado mágico de 4 por 4”.
    Desde entonces he sentido una gran fascinación por este tema, pero no ha sido hasta recientemente que he hecho una investigación más seria sobre los “cuadrados mágicos”, fruto de la cual es este artículo que he dividido en tres partes:
        1. Historia y curiosidades de los cuadrados mágicos.
        2. Características de los cuadrados mágicos y algoritmos de cálculo.
        3. Estrategias de resolución de los cuadrados mágicos, de orden impar o par.
        4. Galeria de cuadrados mágicos.

1. HISTORIA y CURIOSIDADES DE LOS CUADRADOS MÁGICOS

    Parece que los chinos fueron los primeros en descubrir las curiosas propiedades de los cuadrados mágicos, que ellos llamaban “Lo Shu”, y, probablemente, fueran también sus inventores al menos unos cinco siglos antes de nuestra era.
    Una leyenda explica que el primer Lo Shu fue revelado a los hombres dibujada en el caparazón de una extraña tortuga que emergió del río Lo, de aquí su nombre ya que Shu quiere decir “río”.
    En el I Ching, el clásico libro chino de las Mutaciones y de la adivinación, aparece esta imagen del Lo Shu:

                (imagen del Lo Shu)                                                       (Lo Shu en cifras modernas)

     Los chinos, por tanto, les atribuyeron un carácter místico y creían que era un símbolo que reunía los principios básicos que formaron el Universo.
     · Los números pares simbolizaban el principio femenino o Yin.
     · Els números impares simbolizaban el principio masculino o Yang.
     · El número 5 representa la Tierra, a su alrededor están distribuidos los cuatro elementos principales, el agua
1 y 6, el fuego 2 y 7, la madera 3 y 8, los metales 4 y 9.
     Además construyeron cuadrados mágicos de mayor tamaño, hay documentados algunos de orden 6, o sea, formados en un casillero de 6 por 6.

     En Khajuraho (Índia) un templo construido entre los siglos XI y XII tiene un pilar rodeado por una cuadrícula con un cuadrado mágico de orden 4 el cual sería equivalente –traduciendo los caracteres- a la siguiente imagen:
 

     Como se puede observar fácilmente, todas sus filas, columnas y diagonales suman 34. Pero además, sus diagonales “quebradas” (las líneas imaginarias trazadas desde cada número de la primera fila), sus esquinas, sus cuatreo cuadrantes y el cuadrado central también suman 34. Sin duda, un trabajo impresionante de algún matemático hindú.
    Los matemáticos árabes descubrieron los cuadrados mágicos por contacto con esta tradición hindú y también se sintieron fascinados por sus características y, probablemente los difundieron por Occidente durante la Edad Media.
    El casillero de este cuadrado mágico árabe está formado por las letras de la palabra Alà. Todas sus filas, columnas y diagonales suman 66, cifra que en el Islam corresponde al valor numérico de Alà.

( imagen del cuadrado mágico de Alà)

    El matemático Cornelio Agrippa (1486-1555) construyó cuadrados mágicos de órdenes 3 a 9 y les atribuyó un significado astronómico, según él, representaban simbólicamente a los planetas Mercurio, Venus, Marte, Júpiter, Saturno más el Sol y la Luna, respectivamente.
    Durante la Edad Media los cuadrados mágicos se grababan en láminas de plata como amuletos contra la peste negra.
    El gran artista Alberto Durero fue también un distinguido matemático que publicó en 1.525 un tratado sobre la perspectiva, la geometría en tres dimensiones y las secciones cónicas titulado “Introducción a la medida con compás y regla”, en el cual se describe una cicloide por primera vez.
    Además incluyó en su obra “Melencolia-1” uno de los cuadrados mágicos más conocidos y que más han fascinado a los estudiosos del tema.

    La gran variedad de detalles que aparecen en este grabado hacen pensar que representa la insuficiencia del conocimiento humano para alcanzar la sabiduría o para profundizar en los secretos de la Naturaleza. En este grabado aparece también un sólido insólito, probablemente, de su invención.
    La característica más visible de este supercuadrado mágico es que el año en que fue grabado, el 1.514, aparece en su parte inferior. Todas sus filas, columnas y diagonales; sus esquinas, el cuadrado central, sus cuatro cuadrantes y sus diagonales “quebradas” suman 34.
    Algunos matemáticos han querido ver más propiedades en su interior como, por ejemplo:

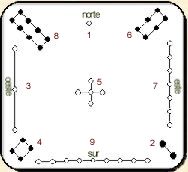
    · Si unimos con líneas los números pares por un lado y los nones por otro, se forman estructuras hexagonales!!

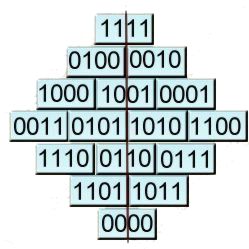
    · Si se traducen sus cifras –restándoles una unidad a cada una, o sea, que quedarían las cifras del sistema hexadecimal (del 0 al 15)- a números binarios y giramos el cuadrado mágico 45º a la derecha aparece una simetría vertical perfecta de ceros y unos, ¡¡cómo si estos se reflejasen en un espejo!!
 

                                              (imagen del cuadrado mágico binario) >>
 

    Los hay que piensan que el cuadrado mágico de Dürer es un “arquetipo lleno de significado y misticismo”.
    Los astrólogos los aconsejaban como amuletos protectores, precisamente, contra la melancolía!

2. CARACTERÍSTICAS DE LOS CUADRADOS MÁGICOS y ALGORITMOS DE CÀLCULO

      Los cuadrados mágicos son estructuras numéricas situadas en una tabla de n filas por n columnas, por lo cual, n se denomina orden del cuadrado, así, por ejemplo, el Lo Shu es un cuadrado mágico de orden 3; el del temple de Khajuraho y el de Dürer son de orden 4.

    Un cuadrado mágico se dice que es “pandiagonal” cuando todas sus diagonales –las dos principales y las “quebradas” en ambos sentidos-  suman la cifra buscada o propuesta.
    Para los musulmanes, durante la Edad Media, los cuadrados mágicos “pandiagonals” de orden 5 con la cifra 1 situada en el centro tenían un significado místico especial, dado que el número 1 es el símbolo de Alá, Ser Supremo y Único.
 

    Observemos, además, que las cuatro esquinas y el centro de este cuadrado también suman 65.
    Un cuadrado mágico se denomina “asociativo” cuando las parejas de números opuestas al centro suman n² + 1.
    Esta es una característica más propia de los cuadrados de orden impar.
    El Lo Shu, presentado anteriormente, es "asociativo" porque, sumando las parejas opuestas al centro, vemos:

     “Lo Shu”:  Ordre 3;  números del 1 al 9;  S(x) =  (33  + 3) / 2 = (27 + 3) / 2 = 15
     “Dürer”:    Ordre 4;  números del 1 al 16;  S(x) =  (43  + 4) / 2 = (64 + 4) / 2 = 34

    Trataré, ahora, de generalizar este algoritmo para cualquier serie aritmética de números.
    Si utilizamos una serie de números que sean múltiplos del l al n², o bien multiplicamos toda la serie numérica por la misma cifra, seguiremos teniendo un cuadrado mágico, pero el resultado obtenido será también múltiplo del resultado inicial.
    Así, si en el Lo Shu utilizamos las cifras pares consecutivas comenzando por el 2, el resultado obtenido en cada línea será 30, por ejemplo: 2 + 10 + 18 = 30, (en lugar de 1 + 5 + 9 = 15), etc.
    Si en el “Dürer” utilizamos los múltiplos de 5, el resultado obtenido será 170:

    También podemos comenzar la serie desde un número a_i en lugar de iniciarla desde el 1, o sea, si sumamos
(o restamos) una determinada cifra t a todos los números de la serie 1 a n² el resultado aumentará n veces la
cifra t sumada. Veamos un par de ejemplos:
    Si sumamos 10 a cada dígito del Lo Shu, entonces la serie comienza en a₁ = 11 y acaba en a_x = 19, el resultado a obtener es: 14 + 19 + 12 = 45 (en lugar de 4 + 9 + 2 = 15)
    Hemos sumado 10 a cada una de las tres cifras y, por tanto, el resultado aumenta en 30 unidades.
    Si sumamos 4 a cada dígito del Dürer, la serie comienza en a₁ = 5 y acaba en a_x = 20, el resultado obtenido es:

    Generalizando todos estos casos, encontramos que el algoritmo de cálculo viene dado por la expresión:

    En la cual, n es el orden del cuadrado, k es la constante del producto y t es la constante de la adición.
    Este algoritmo nos puede resultar de gran utilidad si queremos definir o construir un cuadrado mágico
de cualquier medida y utilizando diversas series de números.

    · Cuestión: Teniendo en cuenta todo esto, podríais calcular para un cuadrado mágico de orden n:

3. ESTRATEGIAS PARA LA RESOLUCIÓN DE LOS CUADRADOS MÁGICOS

    En este capítulo os explicaré como resolver correctamente cuadrados mágicos de cualquier orden utilizando estrategias o técnicas muy sencillas, y probablemente innovadoras (caso del orden par), que son el fruto de una reciente investigación mía.
    Mi objetivo era establecer un sistema manual, es decir, sin la ayuda del ordenador, de normas para resolver o crear cuadrados mágicos de cualquier medida con las siguientes condiciones de uso: rapidez, sencillez, seguridad, mecanización y corrección. Estos métodos son los que presentaré a continuación.
    Es cierto que existen muchas otras soluciones alternativas y de mayor dificultad o belleza a las que encontraremos aplicando estas técnicas, pero se puede considerar que, este, es un “sistema básico”.
    Hemos de distinguir, a la hora de aplicar una estrategia para su construcción, entre los cuadrados mágicos de orden par y los de orden impar.
    Comenzaremos por estos últimos dado que la dificultad para resolverlos es menor.
    El método básico consiste en añadir lateralmente a los cuatro lados series virtuales de casillas, de forma triangular, de manera que nos quede la figura de un rombo. (Paso número 1)
    Entonces, y comenzando desde el extremo superior, situaremos todas las cifras –a partir del 1- siguiendo sólo las diagonales alternas formadas en el rombo, observad que quedan, por tanto, líneas diagonales y casillas interiores del cuadrado en blanco. (Paso número 2)
    El cuadrado mágico se completa situando los números que han quedado en las casillas “virtuales” exteriores del cuadrado, en las casillas interiores en blanco, siguiendo primero una simetría horizontal, las del triángulo superior pasan a completar la parte inferior, como si lo recortásemos y lo pegásemos sin girarlo y las del triángulo inferior en la parte superior; y una simetría vertical, las de la parte exterior derecha en la interior izquierda y al revés. (Paso número 3)
    Esta imagen ilustra claramente este procedimiento:

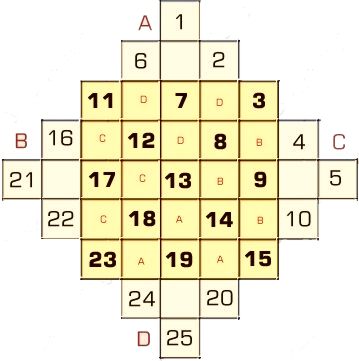
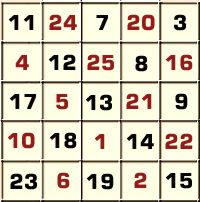
            ¡¡Es increíblemente sencillo!!
 

     Para resolver cuadrados mágicos de orden par seguiremos los siguientes pasos, que son mucho más fáciles de aplicar de lo que puede parecer en un primer momento:
    Utilizaré, en primero lugar, un cuadrado de orden 4, que es el menor de los de orden par, para aclararlo mejor.
    · 1. Comenzaremos por situar el número 1 (o la 1ª cifra de la serie) en el extremo superior izquierda y entonces escribiremos, desplazándonos de izquierda a derecha, sólo las cifras correspondientes a las casillas que forman las dos diagonales principales.

    · 2. Ahora nos situaremos en la primera casilla inferior derecha en blanco, vecina de la del extremo, dónde pondremos el número 2 (o la 2ª cifra de la serie) e iremos desplazándonos hacia arriba y en sentido de derecha a izquierda para ir completando, en estricto orden, las casillas que faltan, es decir, las que forman los interiores de las diagonales principales y las dos casillas exteriores de las filas centrales.
    Es decir, pondremos el 2 e iremos contando de uno en uno hasta llegar a una de las casillas mencionadas, entonces escribimos esta cifra y las seguimos enumerando, si se acaba una fila subimos a la anterior y cambiamos de sentido (zigzag), hasta llegar al extremo superior izquierda.
    De hecho, como se puede observar, el cuadrado mágico de orden 4 ya ha quedado completamente resuelto.
 

    Extrapolaré, a continuación, este método a cuadrados mágicos mayores de orden par.
    Pasaremos, pues, al cuadrado de orden 6 y aplicaremos los dos pasos descritos anteriormente:
 

    · 3b. Finalmente nos situaremos en el extremo inferior derecho y con un desplazamiento de derecha a izquierda, iremos contando de uno en uno y escribiremos sólo los números impares en las casillas correspondientes que han de coincidir exactamente con las casillas que todavía quedaban en blanco.
    (Los pasos 3a y 3b pueden invertirse de orden sin afectar el resultado final)

   Una vez completado este cuadrado mágico de orden 6 se pueden extraer algunas conclusiones, dado que este método es recurrente y sólo varían algunos detalles dependiendo del orden del cuadrado.
    Hay tres factores determinantes o que definen cada paso:
· El primero es indicar el extremo de inicio: Superior (S) / Inferior (I), Derecha (D) / Izquierda (E)
· El segundo el tipo de desplazamiento a seguir: de izquierda a derecha (E-D), de derecha a izquierda (D-E) o en zig-zag (Z-Z)
· El tercero es la acción a aplicar: completar diagonales (DG), interior diagonales (DGI), exterior diagonales centro (DGE), escribir pares (EP), escribir impares (ES), completar números restantes (NR)
    Definidas las normas de aplicación y la nomenclatura abreviada a utilizar, acabaré este capítulo con unas tablas de trabajo abreviadas para completar cuadrados mágicos de orden par (4 al 12).
 

    Existen soluciones alternativas o simétricas, pero este método es básico, correcto y bastante sencillo.

    Carlos Guirado ha contribuido al método expuesto con su artículo titulado "Método Blai"

4. GALERÍA DE CUADRADOS MÁGICOS

    Para acabar con esta exposición, presentaré una modesta colección de cuadrados mágicos, que además de los anteriores, me parecen muy interesantes, curiosos o, incluso, pequeñas obras de arte.
    Ejemplos los hay a millares, y más actualmente ya que con los ordenadores se hallan maravillas, pero he dado preferencia a los compuestos manualmente, llamadme romántico, o que aportan una idea original o estéticamente brillante.
    Algunos son de cosecha propia, otros los he encontrado durante mi investigación...

    Este cuadrado mágico de orden 10 (*) , está formado por los 100 primeros números pares.
    Tiene la propiedad de que la suma de sus filas, columnas y diagonales es igual a 1010  (Déu-Déu).
    Por cierto, el número 1010 en sistema binario es igual al 10 en sistema decimal!!     1010₂ = 10₁₀

 (*) En catalán las palabras Dios y diez son homófonas: Déu y deu

    Este cuadrado mágico está compuesto exclusivamente por los múltiples de 6 en un casillero de 6 x 6 >> (666)
    Tiene la característica principal de que la suma de les sus filas, columnas y diagonales es igual a 666.

    Este cuadrado mágico de orden 12, está formado por los 144 primeros números impares, desde el 1 hasta el 287.
    Tiene la propiedad de que la suma de sus filas, columnas y diagonales es igual a 1728 = 12³.

    Este cuadrado mágico de orden 8, está formado por los números del 1 al 64.
    Tiene la propiedad de que la suma de sus filas, columnas y diagonales es igual a 260, pero también lo es la suma de sus cuatreo esquinas con los cuatro números centrales. La suma total de las casillas blancas y negras es idéntica, las fuerzas se mantienen equilibradas, e igual a 1040.

    Este maravilloso cuadrado mágico de orden 4, tiene la sorprendente característica de ser pandigital, es decir, que cada elemento está formado por las diez cifras decimales sin repetir ninguna y además la suma de sus filas, columnas y diagonales es también pandigital S(x) = 4129607358.
    Probablemente es la matriz pandigital de orden 4 menor posible, dado que se pueden construir otras pero con números mayores.

    Este fantástico cuadrado mágico de orden 6 está compuesto exclusivamente per números primeros.
    La suma sus filas, columnas y todas sus diagonales, es decir es pandiagonal, es igual a 666.

    Hay cuadrados mágicos que pueden tener la notable propiedad de contener otro cuadrado mágico en su interior de orden inferior, por tanto, son cuadrados mágicos dobles. Incluso se pueden construir algunos que contienen sucesivos cuadrados mágicos en su interior en capas concéntricas.
    Aquí os propongo un ejemplo de cuadrado mágico doble de orden 5 que contiene en su interior otro de orden 3.
    La suma de las filas, columnas y diagonales del cuadrado mágico de orden 5 es igual a 75, mientras que las del cuadrado menor de orden 3 es igual a 45.
 

    Estos dos cuadrados mágicos de orden 4 son especulares uno respecto al otro, una cualidad muy rara y destacable. La suma de sus filas, columnas y diagonales es ambos cuadrados de 242, además los dos son pandiagonales.

    Es un cuadrado mágico de nueve casillas formado con los tres primeros números, cambiando su orden en las segundas y terceras líneas/filas, cuyas horizontales y verticales suman siempre seis. También suma seis una de las diagonales. La segunda diagonal suma 9, número que resulta de la operación 6 x 3 = 18, dado su valor absoluto (1 + 8).

Autor: Blai Figueras Álvarez

E-mail: mentaludix@hotmail.com