Introducción a las Ecuaciones Paramétricas

Autor: Luis R. Morera González

En este artículo se definen las ecuaciones paramétricas y se utiliza la calculadora gráfica TI-86 para mostrar su gráfica.

La gráfica de una función en dos variables consiste en la colección de puntos (x,y) en el plano que satisfacen la función. A continuación estudiaremos otra forma de representar estas gráficas.

Sean x = f(t) , y = g(t), donde f y g son dos funciones cuyo dominio común es cualquier intervalo I. La colección de puntos definida por (x,y) = ( f(t),g(t) ) se llama una curva plana. Las ecuaciones: x = f(t) , y = g(t) donde t esta en I, se llaman ecuaciones paramétricas de la curva. La variable t se llama el parámetro. Las ecuaciones paramétricas son útiles para describir movimientos a lo largo de una curva. Suponiendo que la curva esta definida por las ecuaciones paramétricas: x = f(t), y = g(t) , a ≤ t ≤ b donde f y g están definidas dentro del intervalo. Para un valor dado de t, se puede encontrar el valor de x = f(t) y de y = g(t), obteniendo un punto (x,y) sobre la curva. De hecho a medida que t varia dentro del intervalo desde t = a hasta t = b, los valores sucesivos de t dan lugar a un movimiento dirigido a lo largo de la curva, esto es siguen la curva en cierta dirección mediante la sucesión de puntos (x,y) correspondientes “la dirección es inportante”.

Analice la curva definida por las ecuaciones paramétricas: x = cos(t) ; y = sen(t); 0 ≤ t ≤ 2Π.

Utilizando las ecuaciones paramétricas definidas anteriormente, podemos encontrar puntos (x,y) de la curva para los diferentes t en orden “comenzando con t = 0 y aumentando t hasta llegar a t = 2Π”. La siguiente tabla muestra los puntos (x,y) partiendo de t = 0 hasta t = 2 Π.

TABLA 1

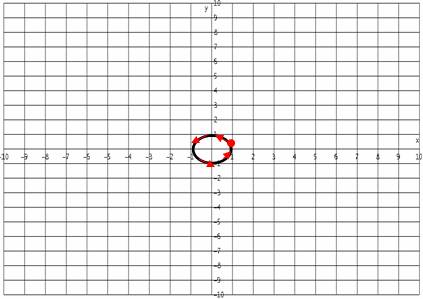
Si ubicamos estos puntos en el plano cartesiano y los unimos mediante una curva suave obtenemos la gráfica de las ecuaciones paramétricas anteriores. Es importante el orden en que se obtienen las soluciones debido ha que al unir los puntos debemos escribir una flecha que nos indique ese orden.

A continuación se muestra la gráfica.

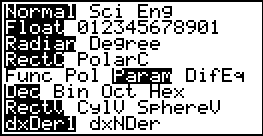
Si utilizamos la calculadora gráfica TI-86 para ver la gráfica de las ecuaciones paramétrcas anteriores, tenemos inicialmente que poner la calculadora en el modo angular de radianes he indicar que estamos trabajando con ecuaciones paramétricas. Esto es así debido a que estamos trabajando con funciones trigonométricas. Para esto entre ha MODE.

Además para tenemos que crear una ventana adecuada en la calculadora antes de ver la gráfica. Para esto seguimos los siguientes pasos entre ha GRAPH, WIND y ponemos por ejemplo:

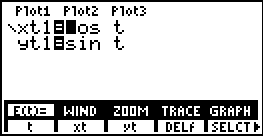
Ahora entramos la ecuación paramétrica en la calculadora, entrando ha GRAPH, E(t).

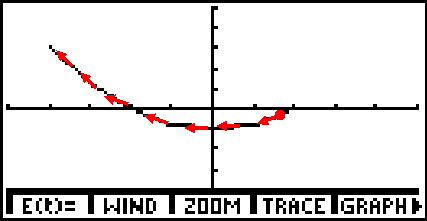
Para ver la gráfica entre a TRACE, para obtener:

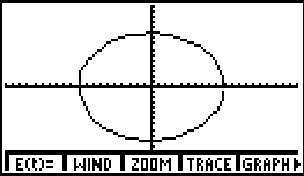
Es importante notar que la calculadora no muestra la gráfica real, es una buena aproximación. Además recuerde que la dirección en la cual se crea la gráfica de las ecuaciones paramétricas es parte de la solución. La calculadora gráfica no muestra la dirección. Para llegar a la solución debemos utilizar la TABLA 1 ó simplemente observar la dirección como se crea la gráfica en la calculadora. La imagen muestra la gráfica de las ecuaciones paramétricas. La flecha con un punto indica donde comienza y la dirección.

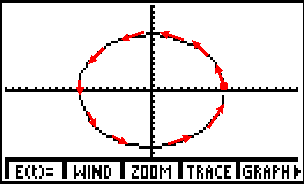
Ahora analizaremos la curva definida por las ecuaciones paramétricas:

x = -2t ; y = t² – 1 ; -1≤ t ≤2.

Utilizando las ecuaciones paramétricas definidas anteriormente, podemos encontrar puntos (x,y) de la curva para los diferentes t en orden “comenzando con t = -1 y aumentando t hasta llegar a t = 2”.

TABLA 2

Si utilizamos la calculadora gráfica TI-86 para ver la gráfica de las ecuaciones paramétrcas anteriores, tenemos inicialmente que poner la calculadora en el modo angular de grados he indicar que estamos trabajando con ecuaciones paramétricas. Para esto entre ha MODE.

Además para tenemos que crear una ventana adecuada en la calculadora antes de ver la gráfica. Para esto seguimos los siguientes pasos entre ha GRAPH, WIND y ponemos por ejemplo:

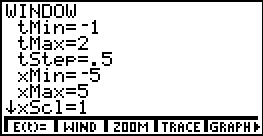
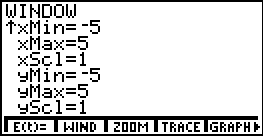
Ahora entramos las ecuaciones paramétricas en la calculadora, entrando ha GRAPH, E(t).

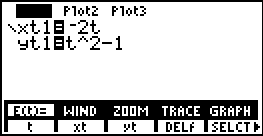
Para ver la gráfica entre a TRACE, para obtener:

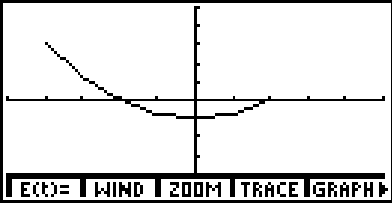
Como aprendimos en el ejemplo anterior esta no es la solución real. La solución real es: