| Unitat 1:á AritmŔtica i └lgebra bàsica. | |
|
PrÓctica
1.1: Operacions elementals |
Pràctica 1.9: Operacions amb polinomis Pràctica 1.10: Valor numèric d'un polinomi Pràctica 1.11: Binomi de Newton Pràctica 1.12: Desenvolupament de potències Pràctica 1.13: Descompondre factorialment un polinomi Pràctica 1.14: Determinació de les arrels d'un polinomi Pràctica 1.15: Operacions amb fraccions algèbriques Pràctica 1.16: Descompondre en fraccions simples |
| Unitat 2:á Anàlisi. | |
| PrÓctica
2.1: Gràfica de funcions en forma explícita Pràctica 2.2: Gràfica de funcions definida a trossos Pràctica 2.3: Gràfica de funcions en valor absolut Pràctica 2.4: Càlcul de límits i continuïtat Pràctica 2.5: Càlcul de derivades Pràctica 2.6: Anàlisi i representació de funcions |
Pràctica
2.7: Càlcul d'integrals indefinides Pràctica 2.8: Funcions primitives Pràctica 2.9: Càlcul d'integrals definides Pràctica 2.10: Càlcul d'àrees Pràctica 2.11: Càlcul de volums Pràctica 2.12: Volum del cilindre, del con i de l'esfera |
| Unitat 3: Àlgebra lineal i Geometria. | |
|
PrÓctica
3.1: Resolució de sistemes |
Pràctica 3.9: Àrea d'un paral·lelogram Pràctica 3.10: Volum d'un paral·lelogram Pràctica 3.11: Equació del pla definit per un punt i dos vectors Pràctica 3.12: Posicions relatives de tres plans Pràctica 3.13: Equació de la recta definida per un punt i un vector Pràctica 3.14: Pràctica 3.15: Pràctica 3.16: |
La finestra de treball de DERIVE PER A WINDOWS consta d'una barra de títols, d'una barra de menus, d'una barra d'eines, de la finestra d'expressions i d'una barra d'estat.

1) La barra de títols
es troba en la part superior de la finestra. A la dreta es troben les tres
icones típiques de minimitzar, maximitzar i tancar.
2) La barra de
menus conté els menus generals, és a dir, Arxiu, Edició,
Editar (Autor), Simplificar, Resoldre, Càlcul, Definir, Opcions, Finestra
i Ajuda.
3) La barra d'eines
conté les icones de les eines. Aquestes són: Nova, Obrir,
Guardar, Imprimir, Borrar expressions, Recuperar,
Renumerar, Editar expressions, Introduir un vector, Introduir
una matriu, Simplificar, Aproximar, Resoldre, Substituir
variables, Calcular límits, Calcular derivades, Calcular
integrals, Calcular sumatoris, Calcular productes, Obrir
la finestra Gràfics-2D i Obrir la finestra Gràfics-3D.
4) La barra d'estat ens informa de l'estat en el que ens trobem. En
el nostre cas, ens indica que la línia activa #3 és la simplificació
de la línia #2.
Per a treballar amb DERIVE cal tenir en compte sempre l'eina Editar expressions, excepte quan es vol treballar matrius i sistemes d'equacions. Quan cliquem en Editar expressions, apareix la finestra:
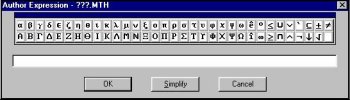
En ella podem
escriure les expressions fent us del teclat o bé dels caracters especials
que la finestra conté. Amb el ratolí podem seleccionar una línia
fent clic en el número de l'expressió, o bé, seleccionar
una part de l'expressió. Un cop elegida l'eina Editar expressions,
amb F3 podem copiarla en la barra oberta i amb F4 podem copiar-la incloent-la
dins un parèntesi.
Entre els caracters
especials tenim el n˙mero pi, el n˙mero e, la unitat imaginÓria i,el símbol
d'arrel quadrada, l'infinit... Si a l'introduir el n˙mero e o bÚ la unitat
imaginària i no els hi posem l'accent circumflexe, és a
dir, ![]() , DERIVE
no els reconeix com a tals i els considera variables.
, DERIVE
no els reconeix com a tals i els considera variables.
Unitat 1:á AritmŔtica i └lgebra bàsica.
PrÓctica
1.1: Operacions elementals
Si volem calcular el valor d'una expressió com ara 125·(43
+ 219) + 215·![]() ,
cal fer:
,
cal fer:
1. Clicar en Editar expressions i escriure l'expressió 125(43
+ 219) + 21^5*112^(1/3) i fer clic en el botó Sí.
2. Clicar en Simplificar/Aproximar. El resultat que s'obté
és: 1,97192·107.
Calculeu
el valor de les expressions:
a) 21·57 - 72·![]()
b) ![]()
c) 3·(-0,2503)6 + 7·(-1,57)4 - 5·2,5252
Pràctica
1.2: Operacions més abançades
Si volem calcular el valor de l'expressió ln![]() - 3·e5-7! + log3 5, hem de fer:
- 3·e5-7! + log3 5, hem de fer:
1. Clicar en Editar expressions i escrivim ln![]() 35
- 3·
35
- 3·![]() ^(5-7!)+log(5,3)
i després fer clic en el botó Sí.
^(5-7!)+log(5,3)
i després fer clic en el botó Sí.
2. Clicar en l'icona Aproximar. El resultat que s'obté és:
3,24264.
Tenint en
compte el procÚs indicat anteriorment, calculeu:
a) 5·e-7 - 3·log(12)
b) 15! - 2·![]() +
+
![]()
c) 7·(-2,5·log 5)2 - 2·(-1,03)ln 4
PrÓctica
1.3: Operacions amb fraccions
Si volem calcular el valor de l'expressió ![]() ,
hem de fer:
,
hem de fer:
1. Clicar en Editar expressions i escrivim 3/5-2(7/3-(2/3)·(3/17))
i després fer clic en el botó Sí.
2. Clicar en l'icona Simplificar. El resultat que s'obté és:![]() .
.
Tenint en
compte el procÚs indicat anteriorment, calculeu:
a) ![]()
b) ![]()
c) 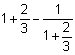
PrÓctica
1.4: Expressions decimals dels n˙meros racionals
Si volem calcular l'expressió amb 12 xifres decimals de la fracció
![]() , hem de fer:
, hem de fer:
1. Anar a Definir/Mode d'operar/Sortida i escrivim en la casella Dígits:
9.
2. Fer clic en Editar expressions i escriure 17/30 i fer un clic en el
botó Sí.
3. Clicar en l'icona Aproximar. El resultat que s'obté és:0,566666666666.
4. Anar a Definir/Mode d'operar/Reajustar tot.
Doneu l'expressió
amb 15 xifres decimals de les fraccions següents:
a) ![]()
b) ![]()
c) ![]()
PrÓctica
1.5: Notaciˇ cientÝfica
Si volem calcular la següent operació 3,47·1013
: 2,07·10-25 i donar el resultat en notació científica,
hem de fer:
1. Anar a Definir/Mode d'operar/Sortida i escrivim en la casella Notació:
Científica i en la cassella Dígits: 8.
2. Fer clic en Editar expressions i escriure 3.47*10^13/(2.07*10^(-25))
i fer un clic en el botó Sí.
3. Clicar en l'icona Simplificar. El resultat que s'obté és:
1,6763285·1023.
4. Anar a Definir/Mode d'operar/Reajustar tot.
Doneu el
resultat de les següents operacions en notació científica:
a) 7,51·10-9 + 3,21·10-7
b) 2,31·1012·5,237·10-5
c) 1,005·1023 :2,031·1032
PrÓctica
1.6: Racionalitzaciˇ
Si volem racionalitzar ![]() ,
hem de fer:
,
hem de fer:
1. Clicar en Editar expressions i escriure 2/(1+![]() 3)
i després fer clic en el botó Sí.
3)
i després fer clic en el botó Sí.
2. Clicar en l'icona Simplificar. El resultat que s'obté és:![]() 3
- 1.
3
- 1.
Tenint en
compte el procÚs indicat anteriorment, racionalitzeu:
a) ![]()
b) ![]()
c) ![]()
PrÓctica
1.7: Resoluciˇ dĺequacions
Si volem resoldre l'equació 2x2 + x - 3 = 0, hem de fer:
1. Clicar en Editar expressions i escriure 2x^2+x-3 = 0 i després
fer clic en el botó Sí.
2. Clicar en l'icona Resoldre i premer en Simplificar. El resultat
que s'obté és: [x = 1,x = -3/2].
Tenint en compte el procÚs indicat anteriorment, resoleu les següents equacions:
a) 3x2 + 5x - 2 = 0
b) x3 - 6x = 0
c) x4 - 5x2 + 6 = 0
PrÓctica
1.8: Resoluciˇ dĺinequacions
Si volem resoldre la inequació 2x2 + x - 3 > 0, hem
de fer:
1. Clicar en Editar expressions i escriure2x^2+x-3>0
i després fer clic en el botó Sí.
2. Clicar en l'icona Resoldre i premer en Simplificar. El resultat
que s'obté és: [x < -3/2,
x > 1].
Tenint en
compte el procÚs indicat anteriorment, resoleu les següents inequacions:
a) 3x2 + 5x - 2 < 0
b) x3 - 6x > 0
c) x4 - 5x2 + 6 < 0
PrÓctica 1.9: Operacions amb polinomis.
PrÓctica 1.10: Valor numŔric dĺun polinomi.
PrÓctica 1.11: Binomi de Newton.
PrÓctica 1.12: Desenvolupaments de potŔncies.
PrÓctica 1.13: Descomposiciˇ factorial dĺun polinomi.
PrÓctica 1.14: Determinaciˇ de les arrels dĺun polinomi.
PrÓctica 1.15: Operacions amb fraccions algèbriques.
PrÓctica 1.16: Descompondre en fraccions simples.
Unitat 2: Anàlisi.
Pràctica
2.1: Representació de funcions en forma explícita
Si volem representar la funció f(x) =![]() , cal fer:
, cal fer:
1. Clicar en Editar expressions i escriure x/(x2-1) i fer
clic en el botó Sí.
2. Clicar en Finesstra 2D. S'obra la finestra Gràfics-2D.
3. Selecionar en el menú Finesta/Mosaic vertical, i escollir Opcions/"Rejilla..."
i en el quadrede dialeg col·locar en Horitzontal: 12 i Vertical:
12.
4. I en la finestra Gràfics-2D, seleccionem Representar graficament.
El resultat que s'obté és:
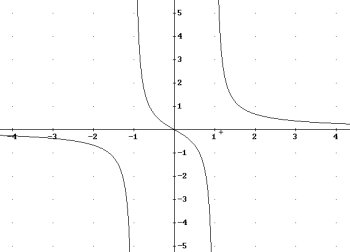
Representeu les funcions:
a) f(x) = x4 - 2x2
b) f(x) = ![]()
c) f(x) = ![]()
Pràctica
2.2: Representació de funcions definida a trossos
Si volem representar la funció f(x) =![]() ,
cal fer:
,
cal fer:
1. Clicar en Esborrar la darrera gràfica i seleccionar Activar
la Finestra àlgebra.
2. Escollir Introduir expressions, i escriure (2x+3)chi(-,
x, 0) + (x^2 -x)chi(0,x,
) i premer
Sí.
3. Escollir Finestra 2D i dins de Gràfics-2D, seleccionar
Representar graficament. El resultat que s'obté és:
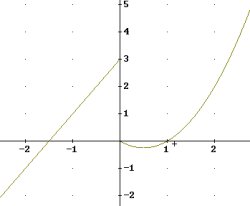
Representeu les següents
funcions definides a trossos:
a) f(x) = ![]()
b) f(x) = 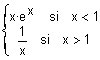
c) f(x) = 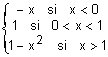
Pràctica
2.3: Representació de funcions en valor absolut
Si volem representar la funció f(x) =![]() x2
+ x - 6
x2
+ x - 6![]() , cal
fer:
, cal
fer:
1. Clicar en Esborrar la darrera gràfica i seleccionar Activar
la Finestra àlgebra.
2. Escollir Introduir expressions, i escriure ABS(x^2+x-6) i premer Sí.
3. Escollir Finestra 2D i dins de Gràfics-2D, seleccionar
Representar graficament. El resultat que s'obté és:
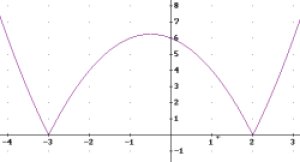
Representeu les funcions:
a) f(x) = ![]() 3x-2
3x-2![]()
b) f(x) = ![]() x2-x
x2-x![]()
c) f(x) = ![]() 1+x-x2
1+x-x2![]()
Pràctica
2.4: CÓlcul de lÝmits i continuïtat
Si volem calcular el límit ![]() ,
farem:
,
farem:
1. Escollir Introduir expressions, i escriure (3x^2-x-2)/(3x^2-5x+2)
i premer Sí.
2. Seleccionar Calcular limits i escriure en Punt: 1 i comprovar
que en Aproximació des de està escollit Ambdós
i clicar Sí.
3. Escollir Simplificar. El resultat que s'obté és: 5.
Si tambÚ volem estudiar
la continu´tat d'aquesta funció en aquest punt, només caldrà
representar la funció, i amb la funció seleccionada, buscar la
imatge d' 1. És a dir:
1. Clicar en Editar expressions
i escriure (3x^2-x-2)/(3x^2-5x+2)
i fer clic en el botó Sí.
2. Clicar en Finesstra 2D. S'obra la finestra Gràfics-2D.
3. Selecionar en el menú Finesta/Mosaic vertical, i escollir Opcions/"Rejilla..."
i en el quadre de dialeg col·locar en Horitzontal: 12 i Vertical:
12.
4. I en la finestra Gràfics-2D, seleccionem Representar graficament.
5. Amb la funciˇ seleccionada, escollir Substituir variables, i escriure
en la casella Substituciˇ: 1, i premer Simplificar.El resultat
és: ?, que s'ha d'interpretar que no existeix. D'aquí es dedueix
que no existeix la imatge, però si el límit. Per tant, la discontinuïtat
en x = 1 és evitable.
Calculeu els límits
següents:
a) ![]() . És
discontuna la funció en el punt x = 2? En cas afirmatiu, quin tipus de
discontinuïtat presenta?
. És
discontuna la funció en el punt x = 2? En cas afirmatiu, quin tipus de
discontinuïtat presenta?
b) ![]() . És
discontuna la funció en el punt x = 0? En cas afirmatiu, classifiqueu
la discontinuïtat.
. És
discontuna la funció en el punt x = 0? En cas afirmatiu, classifiqueu
la discontinuïtat.
c) ![]()
Pràctica
2.5: CÓlcul de derivades
Si volem calcular la derivada de la funció f(x) = x·ex,
idesprés determinar el valor per a x = 0, farem:
1. Escollir Introduir expressions, i escriure x![]() ^x
i premer Sí.
^x
i premer Sí.
2. Seleccionar Calcular derivades i premer Sí.
3. Escollir Simplificar. El resultat que s'obté és: ex·(x+1).
4. Seleccionar la derivada i escollir Substituir variables. Escriure
en Substitució: 0 i premer Simplificar. El resultat és:
1.
Si volem interpretar el resultat de la derivada, farem:
5. Representar la funciˇ f(x) = xĚex tal com hem vist en la prÓctica
2.1.
6. Com la derivada Ús el pendent de la recta tangent en el punt (0,0), la seva
equaciˇ Ús y = x. Si la representem podrem constatar aquest fet.
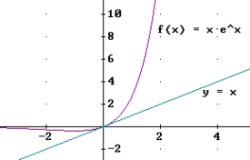
Calculeu les derivades següents
en els punts que s'indiquen:
a) f(x) = ![]() per a x = -2.
per a x = -2.
b) f(x) = sin(ln x) per a x = 1.
c) f(x) = ![]() per a x = 3.
per a x = 3.
I, expliqueu en els tres casos la interpretaciˇ geomŔtrica.
Pràctica 2.6: AnÓlisi i representaciˇ de funcions
Pràctica
2.7: CÓlcul dĺintegrals indefinides
Si volem calcular la integral indefinida ![]() ,
farem:
,
farem:
1. Escollir Introduir expressions, i escriure (x^2+1)![]() ^x
i premer Sí.
^x
i premer Sí.
2. Seleccionar Calcular integrals, seleccionar Indefinida i escriure
en la casella Constant: k, i premer Sí.
3. Escollir Simplificar. El resultat que s'obté és: (x2
- 2x + 3) + k
Pràctica
2.8: Funcions primitives
Si volem calcular la funció primitiva de la funció f(x) =
2x3 - x2 que pren el valor 2 quan x = -1, farem:
1. Calcular la integral indefinida de la funció f(x) = 2x3
- x2 tal com hem fet en la pràctica 2.5.
2. Seleccionar la integral i escollir Substituir variables, i escriure
en Substituir: -1 i premer Sí.
3. Escollir Simplificar. El resultat que s'obté és: k +
5/6.
4. En Introduir expressió copia utilitzant F3 el resultat obtingut
anteriorment, i a continuació escriure = 2, i premer Sí.
5. Seleccionar Resoldre i premer el botó Simplificar. El
resultat és: 7/6 i la funció primitiva és F(x) = 2x3
- x2 + 7/6.
Pràctica
2.9: CÓlcul dĺintegrals definides
Si volem calcular la integral definida ![]() ,
farem:
,
farem:
1. Escollir Introduir expressions, i escriure (x^2+1)![]() ^x
i premer Sí.
^x
i premer Sí.
2. Seleccionar Calcular integrals, seleccionar Definida i escriure
en els límits Inferior: 0 i Superior: 2, i premer Sí.
3. Escollir Simplificar. El resultat que s'obté és: 3·e2
- 3 .
Calculeu les següents integrals definides:
a) ![]()
b)![]()
c) ![]()
Pràctica
2.10: Càlcul d'Órees
Si volem calcular l'àrea compresa pel gràfic de la funció
f(x) = x2 - 6x + 5, l'eix d'abscisses i les rectes x = 0 i x = 3,
farem:
1. Representar la funció f(x) = x2 - 6x + 5 i els rectes
x = 0 i x = 3 tal com hem fet en la pràctica 2.1.
2. Trobar les arrels de f(x), és a dir, en Introduir expressions,
copia utilitzant F3 l'expressió de la funció i escriure = 0,
i premer Sí. La resposta és: x = 1 ja que és lasolució
que es troba dins l'interval [0,3].
3. Seleccionar Calcular integrals, seleccionar Definida i escriure
en els límits Inferior: 0 i Superior: 1, i premer Sí.
4. Escollir Simplificar. El resultat que s'obté és: 7/3.
5. Repetir els apartats 3 i 4 tenint en compte que ara el límit inferior
és 1 i el superior és 3. El resultat és: -16/3 . Com dóna
negatiu, es treu el valor absolut, obtenint: 16/3.
6. Si sumem els dos resultats, tenim l'àrea. El resultat és: 23/3
u2.
Calculeu en cada cas l'àrea
del recinte limitat per...
a) el gràfic de la funció f(x) = ![]() ,
l'eix d'abscisses i les rectes verticals x = 1 i x = 3.
,
l'eix d'abscisses i les rectes verticals x = 1 i x = 3.
b) el gràfic de la funció f(x) = x·ex, l'eix
d'abscisses i les rectes verticals x =-1 i x = 1.
c) els gràfics de les funcions f(x) = x2 - 2x i g(x) = 2x.
Pràctica
2.11: CÓlcul de volums de revoluciˇ
Si volem calcular el volum de revolució que s'obté de girar
entorn l'eix d'abscisses el gràfic de la funció f(x) = x2
- x definida dins l'interval [0,2], farem:
1. Representar la funció f(x) = x2 - x i els rectes x
= 0 i x = 2 tal com hem fet en la pràctica 2.1.
2. En Introduir expressions, i utilitzar F4 per copiar l'expressió
de la funció entre parèntesi, a continuació escriure en
la finestra Editar expressió el número ![]() i elevar la funció al quadrat. Ha de quedar així:
i elevar la funció al quadrat. Ha de quedar així: ![]() (x2
- x)^2, i premer Sí.
(x2
- x)^2, i premer Sí.
3. Escollir Calcular integrals, seleccionar Definida i escriure
en els límits Inferior: 0 i Superior: 2, i premer Sí.
4. Escollir Simplificar. El resultat que s'obté és: 16![]() /15
u3.
/15
u3.
Calculeu en cada cas el
volum de revolució que s'obté de fer girar el gràfic de
la funció entorn de l'eix OX:
a) el gràfic de la funció f(x) = x2 - 2x definida en
[0,3].
b) el gràfic de la funció f(x) = x·ex definida en
[-1,1].
c) els gràfics de les funcions f(x) = 4 - x2 definida en [1,2]
Pràctica
2.12: Volum del cilindre, del con i de l'esfera.
Repetiu la pràctica anterior per determinar el volum del cilindre,
del con i de l'esfera. Tingueu en compte que les funcions que haureu d'utilitzar
en cada cas són:
a) Per al cilidre: f(x) = r, definida en l'interval [0,h].
b) Per al con: f(x) = ![]() x,
definida en l'interval [0,h].
x,
definida en l'interval [0,h].
c) Per a l'esfera: f(x) =![]() , definida en l'interval [-r,r].
, definida en l'interval [-r,r].
Unitat 3: └lgebra lineal i Geometria.
Pràctica 3.1: Resoluciˇ de sistemes amb coeficients constants
Pràctica 3.2: Resoluciˇ de sistemes amb un parÓmetre
Pràctica 3.3: Operacions amb matrius
Pràctica 3.4: CÓlcul de determinants
Pràctica 3.5: Rang dĺuna matriu
Pràctica 3.6: Matriu inversa
PrÓctica 3.7: M˛dul dĺun vector
PrÓctica 3.8: Productes escalar, vectorial i mixt
PrÓctica 3.9: └rea dĺun paralĚlelogram
PrÓctica 3.10: Volum dĺun paralĚlelepÝpede
PrÓctica 3.11: Equaciˇ del pla definit per un punt i dos vectors
PrÓctica 3.12: Posiciˇ relativa de tres plans
PrÓctica 3.13: Equaciˇ de la recta definida per un punt i un vector