XXXIII Olimpíada Matemàtica

• Problema 5
• Problema 6
• Problema 7
• Problema 8

Al pla definim un sistema de coordenades rectangulars. Calculeu l'àrea del
recinte solució del sistema d'inequacions següent:
$$
\left.\eqalign{         | \sqrt{3} y - x | & \leq 2x     \cr
                                 x^2 + y^2 & \leq 2x
              }\right\}        
$$

Busqueu els nombres complexos $ \alpha $ tals que els afixos dels nombres
$ \alpha $, $ \alpha^2 $, $ \alpha^3 $, $ \alpha^4 $ siguin els vèrtexs
d'un trapezi. 

Hi ha una fórmula que dóna l'àrea $ A $ d'un triangle del pla que té els
vèrtexs situats en punts de coordenades enteres com a funció lineal
$ A = aI + bC + dV $ on $ I $ representa el nombre de punts de coordenades
enteres que són interiors al triangle; $ C $ el nombre de punts de
coordenades enteres que queden situars sobre els costats del triangle i
$ V = 3 $ el nombre de vèrtexs de coordenades enteres. Deduïu-la, a partir
de l'anàlisi d'alguns exemples, i demostreu-la.

Anomenarem {\sl polígon mixtilini} una regió tancada del pla limitada per
{\sl costats} que poden ser segments o arcs de circumferència.

Els {\sl angles del polígon mixtilini} es mesuren en graus i són els angles
determinats, en cada vèrtex, pels costats (en cas que siguin segments) i les
tangents traçades pel vèrtex als costats que són arcs de circumferència.

Els {\sl costats del polígon} es mesuren també en graus, de la manera
següent:

\rightline{\vbox{\hsize0.95\hsize\vskip\parskip
\item{$\bullet$}segments: $ 0^{\circ} $
\item{$\bullet$}arcs de circumferència amb la concavitat cap a l'interior
              del polígon: el nombre de graus que mesura l'arc, comptats 
              positivament
\item{$\bullet$}arcs de circumferència amb la concavitat cap a l'exterior
              del polígon: el nombre de graus que mesura l'arc, comptats 
              negativament
}}

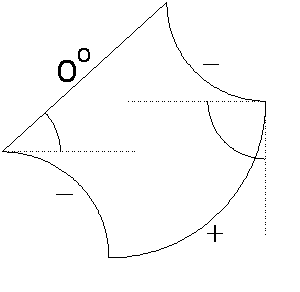
L'esquema i\l·lustra la manera de mesurar els costats i els angles d'un
polígon mixtilini.

{\it a)\ }Demostreu que si un polígon té $ n $ costats, els angles són
          $ A_1 $, $ A_2 $, $ \ldots $, $ A_n $ i els costats $ \alpha_1 $, 
          $ \alpha_2 $, $ \ldots $, $ \alpha_n $ es verifica
          $$
             A_1 + A_2 + \ldots + A_n = \alpha_1 + \alpha_2 + \ldots
             + \alpha_n + (n - 2) \cdot 180^\circ
          $$ 

{\it b)\ }Demostreu que si els tres costats d'un {\sl triangle mixtilini}
          tenen un punt en comú que no és un vèrtex, llavors
          $ \alpha_1 + \alpha_2 + \alpha_3 = 0^\circ $.

{\it b)\ }Si tenim un {\sl angle mixtilini} $ A $ inscrit en una
          circumferència, calculeu $ A $ en funció dels costats $ \alpha $,
          $ \beta $ i $ \gamma $ del triangle que queda determinat a la
          circumferència.

Tornar a la pàgina de la

Tornar a la pàgina d'