Sistema de generadors.

Sigui E un espai vectorial real i sigui un subespai vectorial de E.

Definició:

Direm que el conjunt de vectors és un sistema de generadors de H

Es a dir tot vector de H es pot expressar com a combinació lineal de

Exemple 1:

Aquest vector (1,2) no és l’únic generador d’aquest subespai, també el vector (2,4) o el (3,6) podrien ésser generadors d’aquest subespai. El vector (1,0) no seria un generador de H El vector (0,0) és de H i NO és un generador.

Exemple 2:

Els vectors formen un sistema de generadors deH.

Observació:

Els vectors també formen un sistema de generadors de H

Base d’un espai vectorial i dimensió.

Sigui E un espai vectorial real.

Definició:

Direm que el conjunt de vectors formen una base de E

Exemple 1:

Exemple 2:

Proposició.

Sigui E un espai vectorial real.

formen una base de E

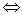Tot vector 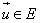s’expressa de manera única com a combinació lineal de

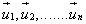
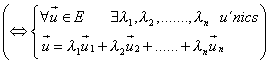
Demostració:

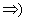Sigui 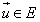com formen base per tant formen un sistema de generadors

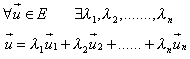
anem a veure que aquesta expressió és única.

Suposem que el vector 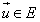tingués dues expressions

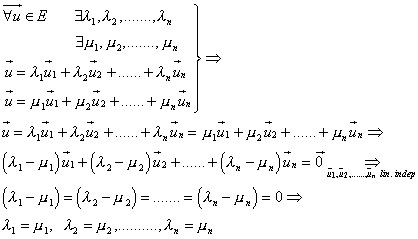
Per tant tot vector 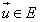s’expressa de manera única com a combinació lineal de

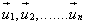
Nota:

Aquesta expressió única d’un vector respecte d’una base ens permetrà definir les coordenades o components d’un vector respecte d’una base.

Dimensió d’un espai vectorial.

Proposició.

Totes les bases de E tenen el mateix número de vectors.

Es a dir si són dues base de E

No fem la demostració

Definició:

Anomenarem dimensió de l’espai vectorial E al número de vectors d’una base i notarem aquest nombre natural per dim E