Subespai vectorial. Introducció.

Exemples de sub-estructures.

Exemple 1:

No té estructura de grup commutatiu ja que no hi ha element oposat.

Exemple 2:

Té estructura de grup commutatiu.

Aleshores direm que és un subgrup de

Definició de Subespai vectorial

Si E és un espai vectorial, direm que 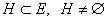és un subespai vectorial de E si en ell podem induir les dues operacions definides en E i respecte aquestes operacions H té estructura d’espai vectoctorial.

1.

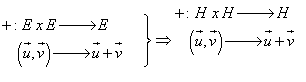
Respecte aquesta operació interna H és un grup abelià

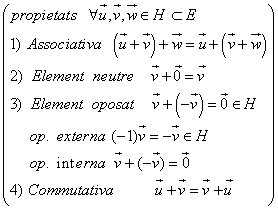
2.

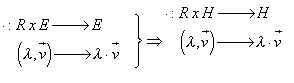
en particular

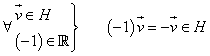
Respecte aquesta operació externa es verifiquen les següents propietats:

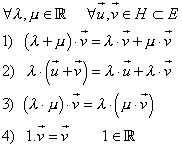
Exemples.

Exemple 1:

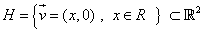
H és un subespai vectorial de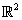

Exemple 2:

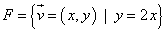
F és un subespai vectorial de

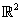
Exemple 3:

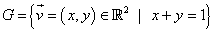
G No és un subespai vectorial de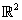

Farem les demostracions després estudiat el teorema de caracterització dels subespais vectorials.

Caracterització dels subespais vectorials.

Teorema.

Si E és un subespai vectorial real i .

Demostració de 1:

condició necessària es compleix sempre.

Demostració de 2:

Observació:

Si E és un e.v i tal que aleshores no pot ser subespai vectorial de E

Demostració:

Exemples.

Exemple 1:

H és un subespai vectorial de

Demostració:

Sigui

Exemple 2:

F és un subespai vectorial de

Demostració:

Exemple 3:

G No és un subespai vectorial de

Demostració: