Una funció és convexa en un interval 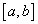 quan la recta tangent al gràfic de la funció en qualsevol punt de quan la recta tangent al gràfic de la funció en qualsevol punt de 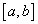 està situada per sota d’aquest gràfic a tot l’interval, excepte en el punt de tangència. està situada per sota d’aquest gràfic a tot l’interval, excepte en el punt de tangència.
Una funció és còncava en un interval 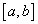 quan la recta tangent al gràfic de la funció en qualsevol punt de quan la recta tangent al gràfic de la funció en qualsevol punt de 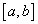 està situada per sobre d’aquest gràfic a tot l’interval, excepte en el punt de tangència. està situada per sobre d’aquest gràfic a tot l’interval, excepte en el punt de tangència.
Direm que un punt 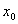 en el qual la funció és contínua i derivable, és un punt d’inflexió quan la funció, en aquest punt, passa de ser còncava a convexa o viceversa. En aquest punt la recta tangent travessa el gràfic. en el qual la funció és contínua i derivable, és un punt d’inflexió quan la funció, en aquest punt, passa de ser còncava a convexa o viceversa. En aquest punt la recta tangent travessa el gràfic.
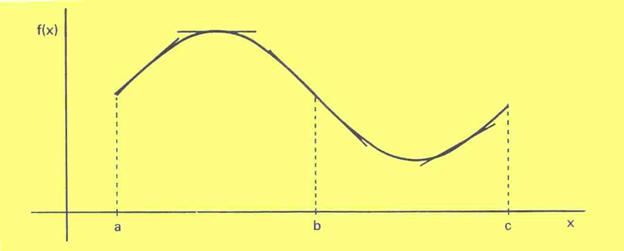
La funció 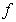 en en 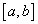 és còncava, les tangents en qualsevol punt d’aquest interval són per sobre la gràfica. és còncava, les tangents en qualsevol punt d’aquest interval són per sobre la gràfica.
La funció 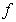 en en 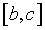 és convexa, les tangents en qualsevol punt d’aquest interval són per sota la gràfica. és convexa, les tangents en qualsevol punt d’aquest interval són per sota la gràfica.
En 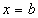 hi ha un punt d’inflexió, la tangent en aquest punt travessa la gràfica. hi ha un punt d’inflexió, la tangent en aquest punt travessa la gràfica.
|

