Els passos per representar gràficament una funció 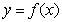 són els següents: són els següents:
- Determinar el domini de
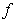
- Trobar els punts de tall amb els eixos de coordenades.
- Simetries
Simetria respecte l’eix OY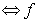 és parell és parell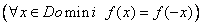
Simetria respecte l’origen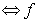 és imparell és imparell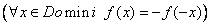
- Periodicitat
Direm que una funció és periòdica de període P
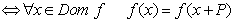
- Intervals de creixement i decreixement, màxims i mínims.
S’estudien els signes de  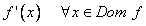
En els intervals en que 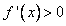 aleshores la funció és creixent. aleshores la funció és creixent.
En els intervals en que 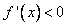 aleshores la funció és decreixent. aleshores la funció és decreixent.
Direm que hi ha un màxim relatiu en 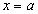 si si 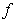 és contínua en és contínua en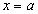 i en aquest punt la funció canvia d’ésser creixent a decreixent. i en aquest punt la funció canvia d’ésser creixent a decreixent.
Direm que hi ha un mínim relatiu en 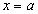 si si 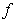 és contínua en és contínua en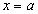 i en aquest punt la funció canvia d’ésser decreixent a creixent. i en aquest punt la funció canvia d’ésser decreixent a creixent.
- Intervals de concavitat i convexitat, i punts d’inflexió.
S’estudien els signes de  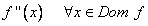
En els intervals que 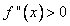 aleshores la funció és aleshores la funció és 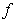 és convexa és convexa 
En els intervals que 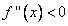 aleshores la funció és aleshores la funció és 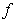 és còncava és còncava 
Direm que hi ha un punt d’inflexió en 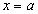 si si 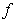 és contínua en és contínua en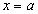 i en aquest punt la funció canvia d’ésser convexa a còncava o alrevés. i en aquest punt la funció canvia d’ésser convexa a còncava o alrevés.
- Asímptotes
Asímptotes horitzontals
Si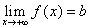 , la recta , la recta 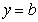 és una asímptota horitzontal del gràfic de la funció és una asímptota horitzontal del gràfic de la funció 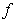
Asímptotes verticals
Si 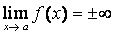 , la recta , la recta 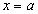 és una asímptota vertical de la funció és una asímptota vertical de la funció 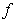
Asímptotes obliqües
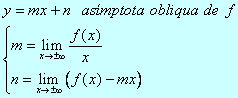
- Fer una taula de valors de la funció f i dibuixar la gràfica.
|