 |
|
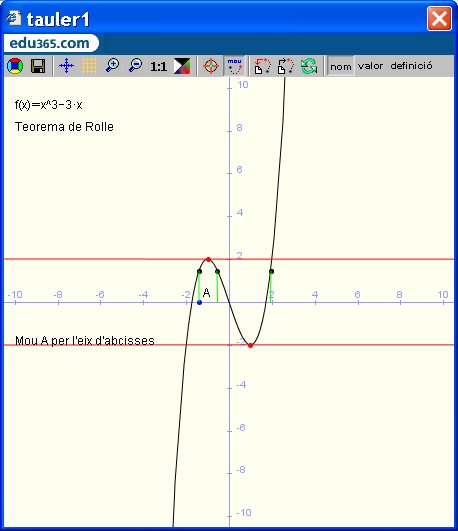
| Teorema de Rolle |
Sigui 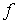 una funció contínua en l’interval una funció contínua en l’interval 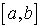 on on 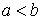 i derivable en l’interval i derivable en l’interval 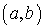 tal que tal que 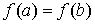 aleshores existeix al menys un número aleshores existeix al menys un número 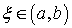 tal que tal que 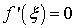 |
| No farem la demostració. |
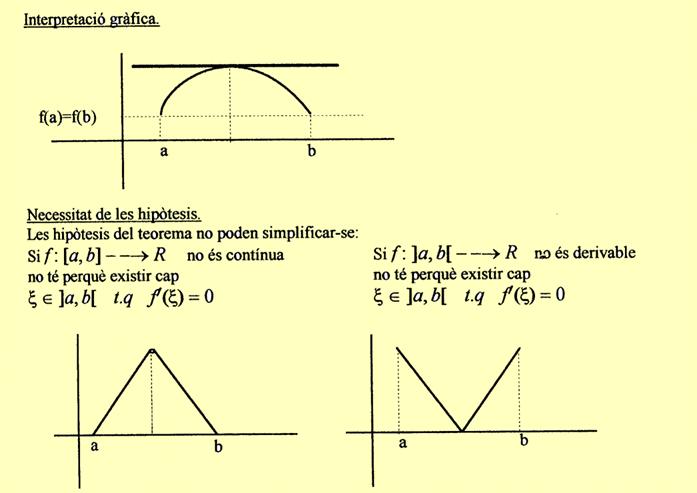 |
Exemple
 |
 |
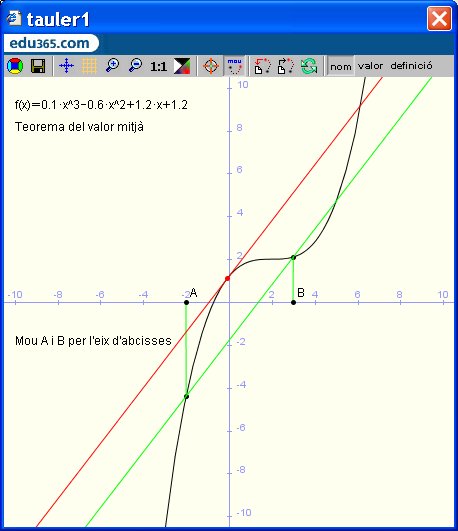
| Teorema del valor mig |
Sigui 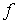 una funció contínua en l’interval una funció contínua en l’interval 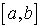 on on 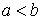 i derivable en l’interval i derivable en l’interval 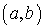 aleshores existeix al menys un número aleshores existeix al menys un número 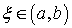 tal que tal que 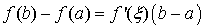 |
| No farem la demostració. |
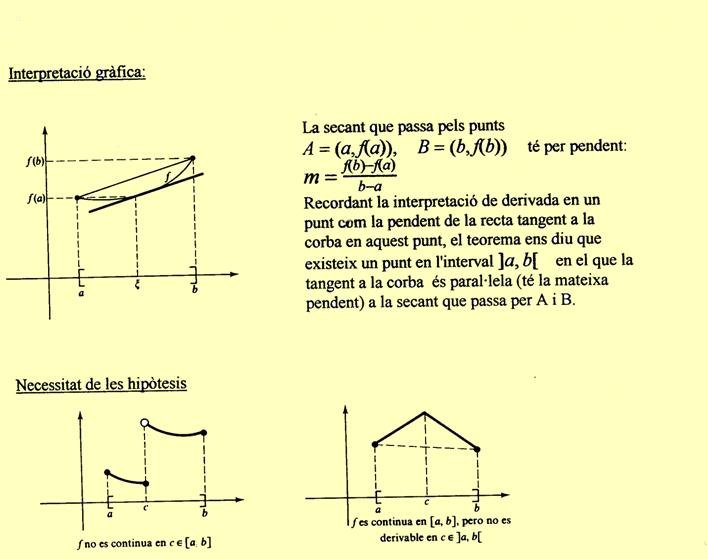 |
Exemple
 |
 |
| Teorema de Cauchy |
Sigui 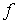 i i 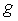 dues funcions contínues en l’interval dues funcions contínues en l’interval 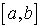 on on 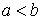 i derivables en l’interval i derivables en l’interval 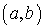 aleshores existeix al menys un número aleshores existeix al menys un número 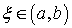 tal que tal que 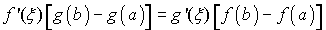 |
| (No fem la demostració) |




