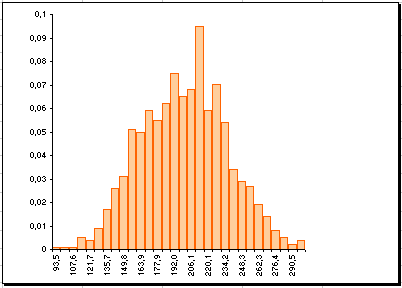
Imaginem que disposem d'un conjunt de 1000 dades tal com les d'aquest arxiu 1000dades.txt

El seu histograma és:

 

La mitjana és 200,2  i la desviació típica 35,6
podem aproximar les dades amb la corba normal de mitjana 200,2 i desviació típica 35,6    N(200,2   35,6)

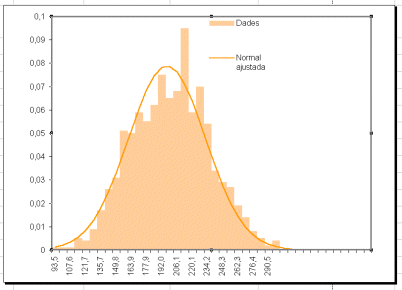
Si ara agrupem les dades de 2 en 2 a l'atzar calculant per cada parella la seva mitjana obtenim 500 valors

Lògicament la mitjana d'aquestes 500 dades és la mateixa que abans 200,2 però la seva desviació és més petita 26,2

La representació de la normal ajustada a aquestes dades agrupada per parelles és:

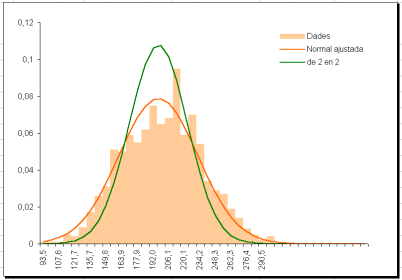
Si agrupem les dades de 3 en 3 a l'atzar tenim que la desviació és 20,6 i la representació:

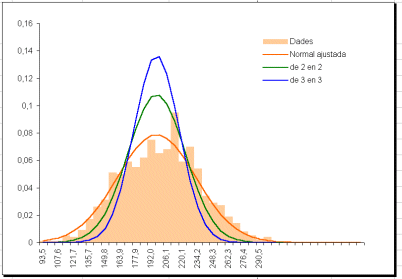
I si les agrupem a l'atzar de 4 en 4 la desviació és 19,4 i la representació:

 

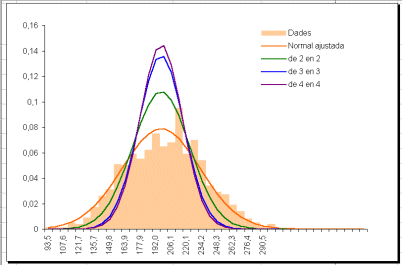
Aquest resultat intuïtiu que es pot repetir amb altres dades recollint l'arxiu d'excel agrup.xls

La variació de la desviació segons la quantitat de dades agrupades ha estat:
 

mesura de l'agrupació	1	2	3	4
desviació típica	35,6	26,0	20,6	19,4

 

La regla teòrica diu que si la desviació típica és s llavors, la desviació de les mitjanes de les agrupacions de mida n és

Fórmula que en el nostre cas dona els valors assenyalats en vermell:
 

mesura de l'agrupació	1	2	3	4
desviació típica	35,6	= 25,2	= 20,5	=17,8

Valors que no estan allunyats dels resultats experimentals