IES Arnau Cadell
Estadística pel batxillerat
La inferència. L'exercici dels botons.

 
Suposem que disposem d'una població de 500  botons (servirien també altres materials ja siguin  pinyes, petxines, bolígrafs o llapissos, fulles, segells, etc. )

Una part de la població de botons que es vol estudiar



Objectiu:

L'objectiu serà l'estudi d'una de les seves característiques a traves de la extracció de mostres

El material permet estudiar:
                    variables qualitatives no numèriques (per exemple: si són de color blanc)
                    variables quantitatives discretes (per exemple: el nº de forats )
                    variables quantitatives continues (per exemple el diàmetre )

Realitzarem d'entrada l'estudi d'aquesta darrera variable: El diàmetre dels botons.

La variable que tractem d'estimar és la mitjana dels diàmetres dels botons que anomenarem 

Aclarirem que en el cas de que algun botó tingui forma diferent a la circular cal prendre com a diàmetre l'amplada màxima.
així per exemple el botó el mesuraríem com s'indica.
 

Cens:

El primer que cal fer és la realització d'un cens, és a dir la ordenació de tots els botons amb l'assignació d'un nº correlatiu a cada un d'ells.
 
 


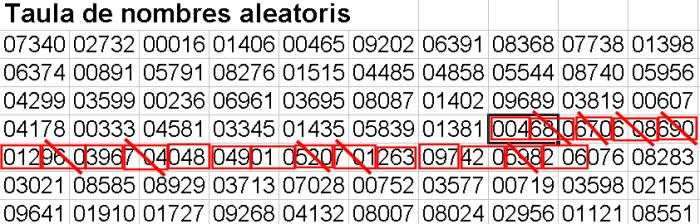
Extracció d'una mostra:

Ara ja podem fer servir la taula de nombres aleatoris (o un altre mètode) per realitzar el sorteig dels botons que formaran la mostra.

La primera mostra que farem serà de mida n = 10

A partir d'un punt de la taula de nombres aleatoris triat a l'atzar agafem correlativament grups de 3 dígits.

Els grups de 3 dígits que formin un nº superior a 500 els descartem.

Hem seguit la taula per files, també la podríem llegir per columnes.

Es continua fins a obtenir 10 números menors de 501.

En aquest exemple han resultats triats els botons 4, 12, 396, 48, 49, 10, 263, 97, 420 i 206

Ara mesurem els botons triats:
 
nº de botó
4
12
396
48
49
10
263
97
420
206
diàmetre
en cm
1,4
1,6
1,1
2
1,8
1,5
2,1
1,1
2,1
1,7

I realitzant els càlculs sobre aquests 10 valors obtenim:
                        La mitjana de la mostra =  = 1,64
                        Desviació típica de la mostra = s = 0,372
 

Interval de confiança del 95%


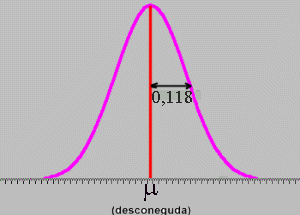
Si obtinguéssim una altra mostra el més probable és que no obtinguéssim exactament aquests mateixos valors

Però la teoria estadística ens diu que els valors de la mitjana mostral formen una distribució normal
                amb  mitjana igual a la mitjana de la població  (que és el que estem cercant)
                i amb desviació típica =   on   és la desviació típica de la població (que per tant no coneixem)

Sense allunyar-nos gaire del valor correcte podem substituir  per s i tindrem 0,118
 

La distribució de les mitjanes mostrals és 

Així recordant la regla del 68-95-99,7 podem dir que el 95% de les mostres tenen la mitjana a l'interval 

[- 2 · 0,118 ,  + 2 · 0,118]

En particular el valor de la mitjana de la nostra mostra (1,64 cm) té una probabilitat del 95% de estar en aquest interval.

En conseqüència l'interval [1,64 - 2 · 0,118  , 1,64 + 2 · 0,118] = [1,40 ,  1,88] té una probabilitat del 95% de contenir la mitjana de la població

Direm que l'interval de confiança del 95 % pel diàmetre mitjà de la població és entre 1,40 cm  i  1,88 cm

Això vol dir que si repetíssim la extracció de moltes mostres, el 95% d'elles donarien un interval en el que hi ha 

i que el  5% de les mostres donarien un interval que no conté 
 

Una mostra de mida 20 tocant una sola tecla.

Si posem les dades en un full de càlcul i escrivim les formules adients  podem fer la feina anterior tocant sols la tecla F9 (=recalcular)

Per exemple:

  

Si recolliu el full de càlcul mostresbotons.xls ho podreu fer vosaltres mateixos (aneu al full 3 d'aquest llibre d'excel)
                                 
100 mostres tocant una tecla

Anem per fi a comprovar l'afirmació que estem fent contínuament :

Existeix una probabilitat del 95% que la mitjana de tots els botons estigui dins aquest interval

Per una costat és fàcil tenir la mitjana dels 500 botons (utilitzeu botons.txt o  botons.xls) és concretament

=1,49

Per una altre costat les possibilitats informàtiques ens donen: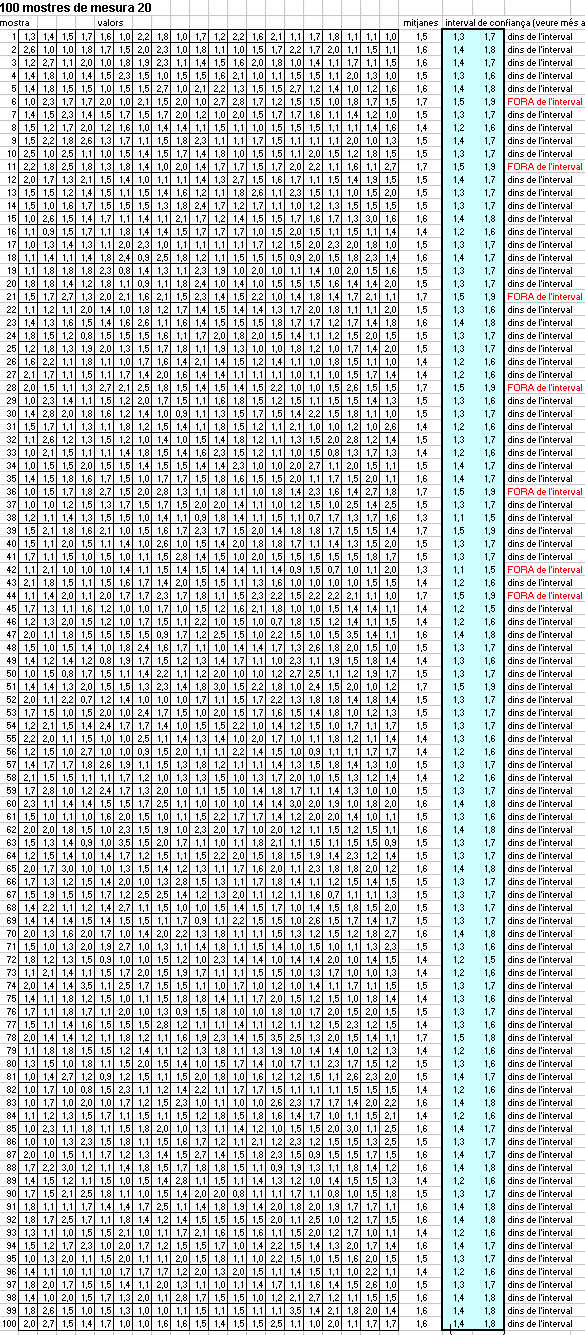

Que és la imatge del que s'obté amb el full de càlcul mostresbotons.xls on podem contar que de 100 intervals de confiança de nivell 95%, 7 (assenyalats amb vermell) no contenen el valor 
                          

Podeu carregar aquest arxiu d'excel i comprovar (al full 4 tocant F9) com recalculant les 100 mostres també s'obté un nivell similar de intervals que agafen el valor 

I per acabar també es pot provar de variar el nivell C de l'interval de confiança (a la cassella K110 del full 4) i  comparar-ho amb  les vegades d'entre les 100 mostres que  cau dins l'interval.