| Aplicaciones educativas de Mathematica |
| Introducción | Investigación educativa con Mathematica | Elementos de utilidad didáctica | Desarrollo de actividades y materiales | Temas afines |
Introducción
En los últimos años hemos podido comprobar como la informática se ha introducido en la enseñanza para dar a los alumnos una formación básica en las nueva tecnologías y como herramienta didáctica. Las aplicaciones didácticas normalmente consisten en programas diseñados especialmente con esta única finalidad y dedicados al estudio de un tema concreto. Actualmente se estudia también, la utilización, en la enseñanza universitaria y no universitaria, de programas orientados a empresas y profesionales o investigadores, aprovechando su potencial a la hora de introducir al alumno en una diversidad de temas, y considerando que su conocimiento es de utilidad para realizar estudios superiores o integrarse en el mundo laboral a un cierto nivel.
En el área de matemáticas o ciencias experimentales, los primeros programas de cálculo usados por los investigadores eran, hasta hace poco, de una complejidad que no permitía su utilización en niveles educativos inferiores, como la educación secundaria. Actualmente, la evolución de programas como Mathematica, ofrece esta posibilidad.
Mathematica, programa desarrollado por la empresa Wolfram Research, es un sistema de computación numérico y simbólico, que incorpora un excelente lenguaje de programación y la capacidad de integrar cálculos, gráficos y texto, en un mismo documento electrónico, llamado cuaderno. Estos y otros elementos de utilidad didáctica del programa, permiten al profesor o usuario de Mathematica, desarrollar actividades educativas a diferentes niveles, aunque en esta página sólo trataremos las aplicaciones en la enseñanza de las matemáticas en educación secundaria.
Investigación educativa con Mathematica
Las aplicaciones de Mathematica en la enseñanza son casi inexistentes en nuestro país y en Europa. En Estados Unidos, donde se desarrolló el programa, existen proyectos como Wave (Web Acces Virtual Education) a nivel de bachillerato o Calculus&Mathematica a nivel superior, que han desarrollado materiales y los han puesto en práctica con alumnos reales. Existen cada año más proyectos y centros que utilizan este programa con finalidades educativas dadas las características del programa que seguidamente exponemos.
Elementos de utilidad didáctica
Diferenciemos los principales elementos de utilidad didáctica del programa en tres niveles, atendiendo a la dificultad de programación y calidad de los materiales que se pueden desarrollar.
Nivel 1:Mathematica se estructura fundamentalmente en dos partes, "Front-End", parte visible del programa, donde además de la barra de menú, encontraremos las ventanas correspondientes a los cuadernos o "notebooks", y el "Kernel" o núcleo, encargado de realizar los cálculos, básicamente. En los cuadernos podemos realizar:
- cálculos numéricos, como en cualquier calculadora, pero casi sin límites, donde podemos determinar el grado de precisión;
- cálculos simbólicos;
- representaciones gráficas en 2 y 3 dimensiones; Ejemplo.
- animaciones, cambio del punto de vista;
- edición de texto;
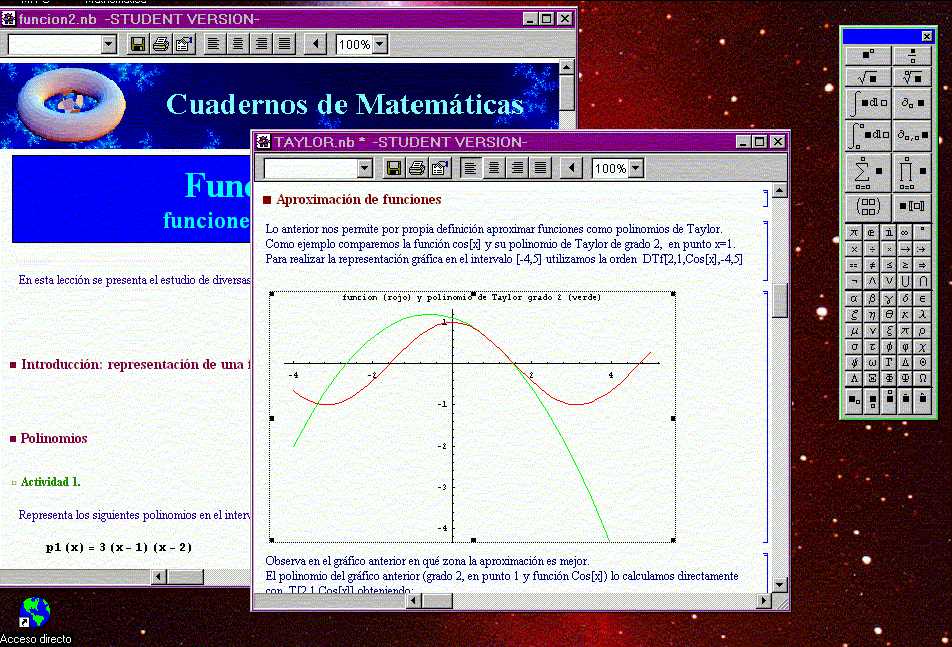
- leguaje de programación, que permite programar funciones específicas de fácil uso para el estudio de conceptos y procedimientos concretos;
- "packages", paquetes de funciones y objetos ya programados, el código de los cuales se incluye en estos archivos, que pueden ser leídos desde el cuaderno, de forma que no interfiere en su presentación;
- diversidad de formatos, algunos de los cuales permiten cargar o leer paquetes y archivos de forma automática al abrir un cuaderno, y ocultar o bloquear partes del cuaderno.
Nivel 3:
Las nuevas versiones de Mathematica, ofrecen otras posibilidades:
- Reconocimiento de los símbolos matemáticos, de forma que podemos introducir una expresión matemática sin traducirla al lenguaje del programa, como hasta ahora.
- Paletas y botones que podemos programar para insertar símbolos o ejecutar funciones de cualquier tipo automáticamente.
- Inserción de "links" con otras partes del mismo cuaderno o externos.
- Nuevas funciones que permiten dar órdenes al "Front-End", desde el núcleo, dando la posibilidad de abrir paletas, u otros archivos, automáticamente al abrir un cuaderno o ejecutar un botón. Ejemplo. También se desarrollaron enlaces, J/Link, que permiten programar desde Mathematica aplicaciones en Java y que a su vez programas o applets de Java puedan interaccionar con un kernel remoto de Mathematica.
- En cada nueva versión podemos encontrar mejoras en los cuadernos, a parte de las habituales como nuevas funciones compiladas, mejoras en la velocidad de cálculo o en los métodos de procesado de imágenes. Una de especial utilidad es el formato cdf.
Al igual que otras aplicaciones similares, en Mathematica los documentos o cuardernos pueden guardarse en formato de documento computable, cdf, y utlizar simplemente un visualizador como CDF Player para visualizar y ejecutar el contenido de forma que no perdamos ninguna funcionalidad. En estos documentos podemos, por ejemplo, modificar parámetros y automáticamente se volverán a calcular los resultados. No es necesario programar una pequeña aplicación Java para cada documento, únicamente basta con guardarlos en formato cdf.
Esto sólo es una muestra de los principales elementos de utilidad a la hora de programar actividades educativas. Para obtener más información técnica o de otras aplicaciones, contactar con Wolfram Research.
Desarrollo de actividades y materiales
Las actividades y materiales también las podemos agrupar en tres grupos, que corresponden básicamente a los niveles del apartado anterior.
- Las dirigidas a alumnos con conocimientos suficientes para realizar las actividades propuestas utilizando las funciones del programa. Normalmente universitarios. En este caso no es necesario realizar ningún tipo de cuaderno ni paquetes de funciones especiales. Nivel 1.
- A nivel 2, el profesor o programador, define una serie de funciones que el alumno utiliza para estudiar un tema concreto. Normalmente es necesario programar funciones para cada tema. O bien, aquellos en que, además, se programa un cuaderno, que incluye las actividades a seguir, definiciones, ejemplos, carga automática del paquete de funciones, ayuda, etc. En este caso, el alumno sólo ha de dominar los elementos básicos del programa.
- Con la versión 3.0 ya podemos programar cuadernos y paquetes de nivel 3, donde el alumno puede seguir las actividades sin entrenamiento previo, disfrutando de toda la potencia y ventajas de Mathematica.
Debemos considerar, también, las nuevas actividades a través de la red Internet, orientadas a la enseñanza de las matemáticas donde se utiliza Mathematica como un motor remoto de cálculo. En estas experiencias se desarrollan cuadernos que posteriormente se convierten a formato HTML (cosa que también se puede hacer desde el mismo programa). Tanto para utilizar el programa en clase o a distancia, es evidente la necesidad de crear cuadernos, dado que habitualmente el alumno no domina el programa.
Para enseñanza secundaria se ha desarrollado una pequeña colección de cuadernos de nivel 3, con el título de "Cuadernos de Matemáticas", que está disponible para todos aquellos profesores con conocimientos de Mathematica que deseen utilizar este programa. Estos cuadernos están disponibles en la página de descarga.
En la actualidad la mayoría de ordenadores soportan la versión 3.0 y posteriores, pudiendo utilizar sin problemas los cuadernos sobre funciones reales, continuidad, derivación y otras muchas aplicaciones como fractales, donde aprovechar todas las ventajas del programa en clase.
Se puede encontrar más material educativo en la base de datos MathSource, donde los usuarios del programa Mathematica, ofrecen sus cuadernos y paquetes.
Los libros y revistas sobre Mathematica se pueden encontrar también en la web de la Wolfram Research.
Si no se dispone del programa, es posible descargar Mathematica Player, para poder visualizar los cuadernos de Mathematica.
Temas afines
| Como podéis ver, el fondo de esta página es la representación de un fractal. También se puede hacer con Mathematica, pero podemos aprovechar la potencia para mapear fácilmente estos gráficos sobre cualquier superficie, como por ejemplo un toro, | 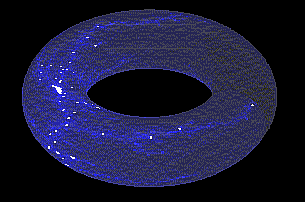 |
conseguir la conocida imagen de la esponja de
Sierpinski, |
|
| o simplemente utilizar el paquete de poliedros para motivar al alumno con imágenes como esta, que él mismo puede crear con la paleta de poliedros. |  |
Funciones que presentan singularidades
Especial atención se ha dedicado al estudio de estas funciones creando utilidades para localizar la presencia de singularidades en las funciones que habitualmente se estudian en enseñanza secundaria y universidad para poder representarlas correctamente. Todas estas funciones están disponibles en los paquetes RLSCF que podéis encontrar en la página de descarga.
 |
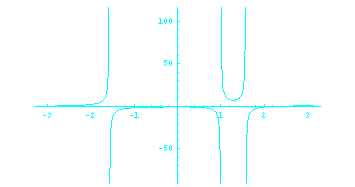 |
Los gráficos anteriores muestran ejemplos de representación de funciones discontinuas en 3D y 2D.
Fernando Gómez Lanza
Página actualizada en Enero de 2012.
Comentarios i sugerencias.