Fractales en Mathematica

La representación gráfica de fractales suele proporcionar unas imágenes de excelente belleza que pueden cambiar notablemente de aspecto con solo modificar la forma de mapear el fractal y su entorno.

En esta página estudiaremos brevemente los fractales de Julia y Mandelbrot, así como la relación entre ambos, sin ánimo de ser rigurosos y dando por supuesto que el lector tiene unos conocimeintos básicos sobre fractales y programación.

Fractal

Podemos considerar que un fractal cumple las siguientes condiciones:

Tiene una estructura geométrica compleja.
Posee autosimilitud o autosemejanza a cualquier escala, tanto geométrica como estadística.
La dimensión fractal o la dimensión de Hausdorff mayor que la topológica.

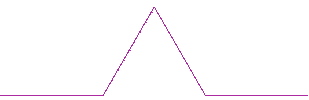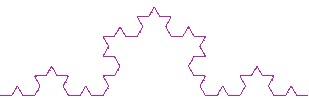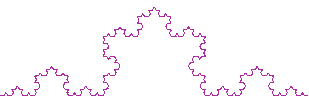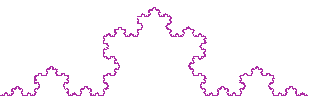Un ejemplo sencillo de fractal lo encontramos en la curva de Koch. Esta curva la podemos construir si reemplazamos sucesivamente cada segmento de la figura por la figura inicial como muestra la animación adjunta.

Este procedimiento puede aplicarse a figuras u objetos de más dimensiones obteniendose otros objetos fractales. Casos parecidos al anterior los encontramos en la alfombra y en la esponja de Sierpinski pero, a diferencia de estos fractales de los que ya conocemos su patrón, en la mayoría de los casos es necesario estudiar su geometría con detalle para encontrar algún tipo de autosemejanza.

Existen otras formas de encontrar objetos fractales de las que sólo trataremos aquellas que nos permiten encontrar los fractales de Julia y Mandelbrot.

Fractales en el plano complejo

Situandonos en el plano complejo podemos aplicar alguna función, f(z), sucesivamente, o sea, aplicar la composición (fºfºfº^...ºfºf)(z) a todos los complejos z. Todos aquellos puntos que después de aplicarles tal operación proporcionen un complejo cuyo módulo converja, una vez representados, formarán la figura de un fractal si cumplen las condiciones enunciadas anteriormente.

Evidentemente no todas las funciones proporcionan un fractal pero, como ya sabemos, encontrar los conjuntos de Julia y Mandelbrot es bastante sencillo. En ambos casos se puede partir de la misma función g(z,z'), tal que, para cada punto del plano complejo, z', encontraremos un conjunto de Julia asociado, J(z'), mientras que si tomamos como origen g(0,z') obtendremos el conjunto de Mandelbrot, M.

Programación

Los programadores que deseen representar estos fractales deben realizar un procedimiento que recorra el plano variando el punto z, en el caso de J(z') con un z' fijo y, en el caso de Mandelbrot variando z'. Además, debe evaluarse la convergencia, o no, cuando se han realizado un número suficiente de composiciones, y en caso de divergencia, aunque puede generalizarse a todos los casos, puede calcularse un valor que indique a qué "velocidad" se va al infinito. Este valor se utilizará posteriormente para asignar un color al punto calculado.

En Mathematica podemos definir una función que realice el procedimiento anterior y representarla directamente utilizando DensityPlot. Para mejorar su presentación utilizaremos alguna función de color de las existentes o programaremos alguna que trabaje en la paleta deseada.

La web de Wolfram Research dispone de numerosos ejemplos y algunos paquetes que pueden ayudar tanto en la programación como en el estudio de objetos fractales.

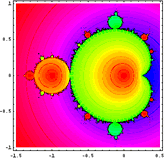		Fractal de Mandelbrot representado directamente en el primer caso y utlizando un programa más elaborado en el segundo que colorea en negro el interior del conjunto M y los puntos que divergen rápidamente, mientras que tiende a aumentar el brillo en la frontera.
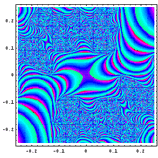		Aunque no lo parezca ambos gráficos corresponden al fractal de Julia en la misma zona del plano complejo. Si en el gráfico de la derecha se hubiera utilizado algún tipo de suavizado adicional en el mapeado o función de color, identificarlos habría sido más difícil.

Una vez que sabemos programar y presentar los resultados de estos y otros fractales, nos podemos dedicar a observar la existencia de autosimilitud o la relación entre los fractales de Julia y Mandelbrot.

Fractal de Mandelbrot

Ampliando una de las ramificaciones superiores del conjunto de Mandelbrot podemos comprobar la existencia de autosimilitud como muestra la figura siguiente.

$Ampliación de la parte superior del fractal de Mandelbrot$

Fractales de Julia

Recorriendo los puntos cercanos a la frontera del conjunto de Mandelbrot, podemos calcular el fractal de Julia asociado y representarlo gráficamente.

Comentario	Imagen del fractal de Julia
El primer punto z' está situado muy cerca del eje real, por tanto, su parte imaginaria es practicamente nula.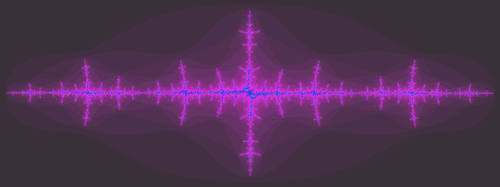
El punto z' se encuentra en una zona exterior al conjunto M pero, casi rodeado por su la frontera.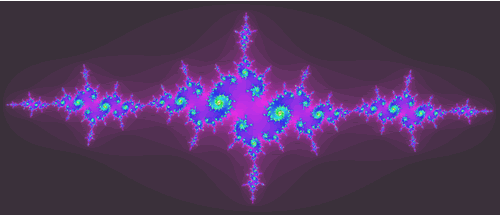

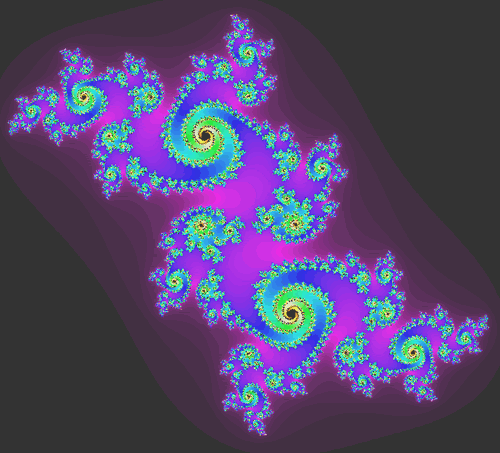
Este y el siguiente caso toman un z' situado en una de las "ramificaciones" exteriores al conjunto M.


El punto z' está en el interior del conjunto de Mandelbrot.
En este último caso z' se encuentra alejado de la frontera y en el exterior.