DISTRIBUCIONES NORMALES DE PROBABILIDAD

CONCEPTOS PREVIOS

Variables aleatorias

· Cuando en un experimento aleatorio se asocia a cada resultado posible un valor numérico, se dice que se ha definido el experimento mediante una variable aleatoria. Las variables aleatorias suelen representarse por letras mayúsculas (X, Y, Z, N, etc.). Los números que toman dichas variables se representan con letras minúsculas (x, y, z, ...)

Ejemplos:

1. El experimento consistente en cobrar 3 euros si sale 1 ó 2 en el lanzamiento de un dado, cobrar 1 euro si sale 4, 5 ó 6, y pagar 5 euros si sale un 3, puede representarse mediante la v.a. X que toma solamente los valores 1,3 y -5. El suceso X=3 estaría representado por los resultados 1, 2; si el dado es perfecto, la probabilidad de tal suceso sería p(X=3) = 2/6.

2. El experimento consistente en observar la duración en horas de las bombillas de una determinada marca puede representarse mediante una v.a., X, que podría tomar, teóricamente, cualquier valor positivo y el 0 (ya que una bombilla puede fundirse en el instante mismo de probarla). En este caso, como los valores posibles de la v.a. son infinitos, hemos de aceptar como natural que la probabilidad de cada valor concreto sea 0. Por ejemplo, admitiríamos que la probabilidad de que una bombilla dure exactamente 2’5 horas vale 0, es decir, p(X=2’5) = 0; en casos como éste sólo admitiríamos probabilidades positivas para intervalos; por ejemplo, en vez de p(X=2’5), podríamos referirnos a p(2’4<X<2’6)

· Variable aleatoria discreta

Las v.a. como la del ejemplo 1 se llaman discretas: toman sólo un número finito de valores.

· Variable aleatoria continua

Las variables como la del ejemplo 2 se llaman continuas: pueden tomar todos los valores de un intervalo. Para su estudio matemático, se utilizan dos funciones, la función de densidad y la función de distribución, cuyas definiciones son las siguientes.

Función de distribución de la v.a. X	Función de densidad de la v.a. X
Se define así, para cada número real x,	Es la derivada de la función de distribución:

Para entender mejor el concepto de función de densidad, hay que pensar en la representación gráfica de variables estadísticas continuas mediante histogramas.

Histograma

En la realidad, al estudiar una variable estadística se recoge una muestra adecuada del colectivo a investigar. Si la variable es continua, se agrupan primero sus valores en intervalos llamados intervalos de clase, como representante de cada intervalo se toma su centro (marca de clase), y se señalan los intervalos sobre el eje X.

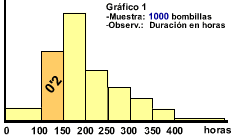
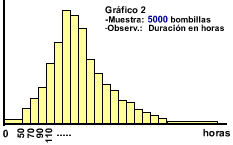
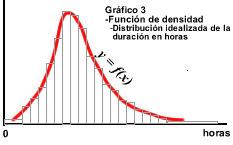
Después, en cada intervalo se levanta un rectángulo de área igual, o proporcional, a su frecuencia (recuerda: frecuencia es el número de veces que el resultado observado cae en el intervalo, dividido por el número de elementos de la muestra; la suma de las frecuencias da 1). La figura final obtenida se llama histograma. Por ejemplo, si de 1000 bombillas observadas, 200 duraron entre 100 y 150 horas, la frecuencia del 125 (marca del intervalo) será 200/1000 = 0’2, y sobre el intervalo [100,150] se levantaría un rectángulo de área igual a 0’2 (gráfico 1). Es importante entender esto: La suma de las áreas de estos rectángulos será 1, puesto que es precisamente la suma de las frecuencias relativas; además, como en estos casos la probabilidad se identifica con la frecuencia, la probabilidad de cada intervalo será igual al área levantada sobre él. Si cogiéramos muestras cada vez mayores y fuéramos reduciendo la amplitud de los intervalos (gráfico 2), el histograma iría delimitando cada vez más claramente una curva continua “ideal”. Esta curva (gráfico 3, en página siguiente) 1. Sería la gráfica de la llamada función de densidad, y 2. Nos daría la probabilidad de un intervalo cualquiera como área bajo la curva en ese intervalo, y 3. El área total bajo la curva valdría 1.

	.
Área A = Área B Gran dispersión de los datos (s grande)	Área A = Área B Poca dispersión de los datos (s pequeño)

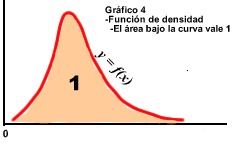
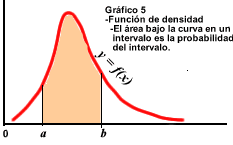
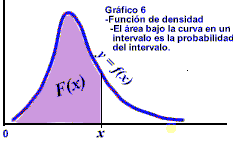
No olvides esto:

1. La gráfica de la función de densidad es el resultado de idealizar en forma de curva la apariencia del histograma (gráfico 3)

2. Como consecuencia, el área total bajo la función de densidad vale 1 (gráfico 4), y además el área bajo la curva en un intervalo representa la probabilidad de que la variable aleatoria tome sus valores dentro de dicho intervalo (gráfico 5).

3. El área bajo la curva antes del valor x es el valor de la función de distribución F(x) (gráfico 6).

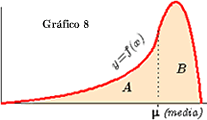
4. La media de la variable aleatoria X es el número x cuya vertical divide en 2 partes de igual área la extensión total bajo la curva (La media de una variable X suele simbolizarse con la misma letra y una raya encima, ; pero ya que en libro recomendado se utiliza la letra , la usaremos también aquí)

5. La desviación típica (llamada en el libro desviación estándar) indica si los valores de la v.a. están muy concentrados, o no, alrededor de la media; se designa con la letra . Si vemos en la gráfica una gran concentración en torno a la media, el valor de es pequeño (gráfico 8)

Distribuciones normales

Las distribuciones continuas más importantes son las llamadas distribuciones normales (gráfico 9): sus gráficas tienen forma de campana perfectamente simétrica respecto de la media, y sus valores están probabilísticamente repartidos del siguiente modo: · El 68’2% de sus valores caen entre , es decir, · El 95’4% de sus valores caen entre · El 99’7% de sus valores caen entre

¿Ejemplos de variables que siguen una distribución normal?

· La distribución de las alturas de los habitantes de una población, del mismo sexo, raza y edad.

· Los coeficientes de inteligencia de los habitantes de una población, del mismo sexo y edad.

· La distribución de los errores aleatorios cometidos al hacer pesadas con una balanza.

¿Hay alguna distribución normal que tenga “la mayor importancia”?

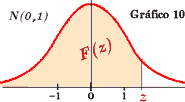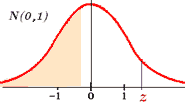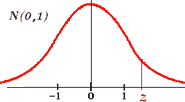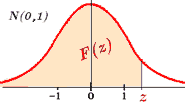
Entre las distribuciones normales, es imprescindible conocer la normal estándar (o reducida), que es la de media 0 y desviación típica 1, es decir, la normal N(0,1). Su función de densidad se indica en el gráfico 10. Su importancia radica en las dos razones siguientes: 1. Existe una tabla con los valores de su función de distribución, o sea, con las probabilidades . 2. Las probabilidades referentes a las demás distribuciones normales se calculan usando la tabla de la normal estándar.

Normal estándar: Área antes de z

Tabla de probabilidades de la normal estándar

Para el cálculo con negativos, se usa que . Así,

z	0	1	2	3	4	5	6	7	8	9
0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199	0,5239	0,5279	0,5319	0,5359
0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596	0,5635	0,5675	0,5714	0,5754
0,2	0,5793	0,5832	0,5871	0,5910	0,5948	0,5987	0,6026	0,6065	0,6103	0,6141
0,3	0,6179	0,6217	0,6255	0,6293	0,6331	0,6368	0,6406	0,6443	0,6480	0,6517
0,4	0,6554	0,6591	0,6628	0,6664	0,6700	0,6736	0,6772	0,6803	0,6844	0,6879
0,5	0,6915	0,6950	0,6985	0,7019	0,7054	0,7088	0,7123	0,7157	0,7190	0,7224
0,6	0,7258	0,7291	0,7324	0,7357	0,7389	0,7422	0,7454	0,7486	0,7518	0,7549
0,7	0,7580	0,7612	0,7642	0,7673	0,7704	0,7734	0,7764	0,7794	0,7823	0,7852
0,8	0,7881	0,7910	0,7939	0,7967	0,7996	0,8023	0,8051	0,8078	0,8106	0,8133
0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289	0,8315	0,8340	0,8365	0,8389
1,0	0,8413	0,8433	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621
1,1	0,8643	0,8665	0,8686	0,8703	0,8729	0,8749	0,8770	0,8790	0,8810	0,8830
1,2	0,8849	0,8869	0,8888	0,8907	0,8925	0,8944	0,8962	0,8980	0,8997	0,9015
1,3	0,9032	0,9049	0,9066	0,9082	0,9099	0,9115	0,9131	0,9147	0,9162	0,9177
1,4	0,9192	0,9207	0,9222	0,9236	0,9251	0,9265	0,9279	0,9292	0,9306	0,9319
1,5	0,9332	0,9345	0,9357	0,9370	0,9382	0,9394	0,9406	0,9418	0,9429	0,9441
1,6	0,9452	0,9463	0,9474	0,9484	0,9495	0,9505	0,9515	0,9525	0,9535	0,9545
1,7	0,9554	0,9564	0,9573	0,9582	0,9591	0,9600	0,9608	0,9616	0,9625	0,9633
1,8	0,9641	0,9649	0,9656	0,9664	0,9671	0,9678	0,9686	0,9693	0,9699	0,9706
1,9	0,9713	0,9719	0,9726	0,9732	0,9738	0,9744	0,9750	0,9756	0,9761	0,9767
2,0	0,9772	0,9778	0,9783	0,9788	0,9793	0,9798	0,9803	0,9808	0,9812	0,9817
2,1	0,9821	0,9826	0,9830	0,9834	0,9838	0,9842	0,9846	0,9850	0,9854	0,9857
2,2	0,9861	0,9864	0,9868	0,9871	0,9875	0,9878	0,9881	0,9884	0,9887	0,9890
2,3	0,9893	0,9896	0,9898	0,9901	0,9903	0,9906	0,9909	0,9911	0,9913	0,9916
2,4	0,9918	0,9920	0,9922	0,9925	0,9927	0,9929	0,9931	0,9932	0,9934	0,9936
2,5	0,9938	0,9940	0,9941	0,9943	0,9945	0,9946	0,9948	0,9949	0,9951	0,9952
2,6	0,9953	0,9955	0,9956	0,9957	0,9959	0,9960	0,9961	0,9962	0,9963	0,9964
2,7	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972	0,9973	0,9974
2,8	0,9974	0,9975	0,9976	0,9977	0,9977	0,9978	0,9979	0,9979	0,9980	0,9981
2,9	0,9981	0,9982	0,9982	0,9983	0,9984	0,9985	0,9985	0,9985	0,9986	0,9986
3,0	0,9987	0,9987	0,9987	0,9988	0,9988	0,9989	0,9989	0,9989	0,9990	0,9990
3,1	0,9990	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993
3,2	0,9993	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995
3,3	0,9995	0,9995	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997
3,4	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9998
3,5	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998
3,6	0,9998	0,9998	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
3,7	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
3,8	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
3,9	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000

Ejercicios (utilización directa de la tabla de la normal estándar)

Llamemos Z a la variable N(0,1). A partir de la tabla de la normal estándar, calcula la probabilidad indicada en los casos a), b), c), d), y el valor de k en e) y f): a) b) c) d) e) f)

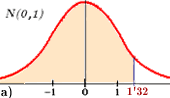
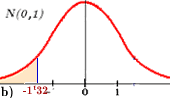
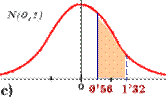
Solución a) El valor de figura en la tabla, en el cruce de la fila 1’30 con la columna 2. Fíjate, el valor es 0,9066. Por tanto, = 0,9066 b) Como en la tabla sólo figuran valores positivos, hemos de pasar de –1’32 a un positivo. Pero, es fácil si te fijas en las dos figuras a) y b), pues en ellas se ve que = . Según la figura a), =(Área total bajo curva) -= 1- Por tanto, = 1-0,9066 = 0’0934 c) No olvides esta fórmula: . Aplicada aquí, dará d) Tal como hemos razonado en el apartado b), =(Área total bajo curva) -= 1-=0’0934 e) Si te fijas en la tabla, el valor más pequeño que aparece es el 0’5000, y concretamente se tiene que . Como el valor que nos da el enunciado, el 0’7291, es mayor que 0’5000, el número k será positivo y debemos encontrarlo directamente como cruce de una fila y una columna. Como puedes comprobar, está en el cruce de la fila 0’6 y la columna 1. Por tanto, k=0’61 f) significa . De aquí resulta Ahora bien, como 0’3772 es inferior a 0’5000, el valor de k será negativo, luego no figurará en la tabla; sin embargo, su opuesto, -k, figurará, y tenemos que En la tabla, el valor 0’6228 nos dice que el número –k está entre 0’31 y 0’32. Pondremos, aproximadamente,

¿Cómo utilizar la tabla de la normal estándar con otras distribuciones normales?

Si consideramos una normal general de media m y desviación s, o sea, la normal X = N(m,s ), para calcular probabilidades usando la tabla de la normal estándar, debemos empezar haciendo el siguiente cambio:

es decir,

Este cambio es importante porque la variable Y que así se obtiene es precisamente la normal estándar Z = N(0,1), con lo que los valores para Y se obtendrán con la tabla estándar. Fíjate en el siguiente ejercicio cómo se procede.

Ejercicio (utilización de la tabla estándar para una normal general)

· Suponiendo X = N(5,2), calcular

Solución

.

Por tanto,

¿Algunas aplicaciones de las distribuciones normales?

· Lee las páginas 339, 340 y 341 del libro recomendado (EDEBÉ, Matemàtiques I, edición 2002); más exactamente, los ejemplos 5 y 6.

¿Ejercicios recomendados?

Hemos procurado con todo este resumen que entendieras la distribución normal sin necesidad de verte obligado a adquirir previamente todo el bagaje matemático necesario para entrar en ella con un poco de profundidad y rigor. Ahora, creeemos que ya puedes entender, y resolver, los siguientes ejercicios del libro mencionado más arriba:

· Ejercicio A, página 342

· Ejercicios C y D, página 343

· Ejercicio 19, página 344

· Ejercicios 21, 24, 25, 26, 31 página 345