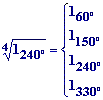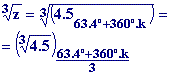NOTA 1: Si algún
resultado se te sale de la escena, puedes disminuir la escala o mover los ejes
con los botones de la parte superior.
NOTA 2:
Si en los
distintos apartados salen en gris las escenas, clica
aquí para instalar el plugin de Java a través de
Internet.
7 Radicación
de números complejos
Ya sabes que la operación de radicación
es la inversa que la de potenciación.
EJEMPLO
1
En la escena siguiente, te presentamos el número complejo
z = 230º y su potencia cúbica
z3 =
(230º)3
= 890º .
Pues bien, vas a comprobar que hay más complejos que elvados al cubo
dan 890º.
Para ello, haz lo siguiente (recuerda que la escena inicial muestra que (230º)3
= 890º):
|
|
- Introduce como argumento de z el valor
A = 150º y pulsa ENTER.
Como verás, no cambia el resultado inicial 890º
Y eso es así, porque (2150º)3
= 8450º = 890º+360º = 890º
- Introduce como argumento de z el valor A
= 270º y pulsa ENTER. Como verás, no
cambia el resultado inicial 890º
Ello es así porque (2270º)3
= 8810º = 890º+2.360º = 890º
- Acabas, así, de comprobar que hay como mínimo
3 números complejos, 230º
, 2150, 2270º,
cuyo potencia 3 vale 890º
Lo cierto es que son esos 3 números complejos los únicos
cuya potencia 3 vale 890º
(Si no has llimpiado la pantalla, podrás ver también
que los extremos de esos vectores forman un triángulo equilátero.)
Por tanto, podremos decir que
| El complejo z
= 890º tiene exactamente 3 raíces
cúbicas, y los afijos de éstas forman un triángulo
equilátero cuyo centro es el origen de coordenadas. Las 3
raíces cúbicas tienen por módulo la raíz
cúbica del módulo, y el argumento de una de esas raíces
se obtiene dividiendo por 3 el argumento de z |
|
EJEMPLO
2
1.
Pulsa
el botón inicio
2.
Introduce r=1, A=60º, n=4 y a continuación
pulsa ENTER
3.
Pulsa el botón limpiar
4.
Ahora tendrás que (160º)4
= 1240º
5.
Introduce A=150º y pulsa ENTER
6.
Ahora tendrás que (1150º)4
= 1600º = 1240º+360º
= 1240º
7.
Introduce A=240º y pulsa ENTER
8.
Ahora tendrás que (1240º)4
= 1960º = 1240º+2*360º
= 1240º
9.
Introduce A=330º y pulsa ENTER
10. Ahora tendrás que (1330º)4
= 11320º = 1240º+3*360º
= 1240º |
Por lo tanto,
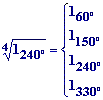
|
De estos dos ejemplos parece deducirse que la
raíz cúbica tiene tres
soluciones, y la raíz cuarta, tiene
cuatro. Pues bien, así sucede en realidad,
y, lo que es más. sucede con cualquier raíz, de cualquier índice:
Si z
es un complejo diferente de 0, entonces tiene n raíces enésimas.
Además
- Todas las raíces enésimas tienen el mismo módulo
(igual a la raíz enésima del módulo de z),
y
- el argumento
de una de ellas se obtiene dividiendo por n el arg(z); los
demás argumentos se van obteniendo sumando 360/n |
Clica aquí
para ver otro applet de raíces enésimas
Calcularemos 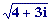 fijándonos al mismo tiempo en la siguiente escena:
fijándonos al mismo tiempo en la siguiente escena:
|
|
- Primero, pasamos z=4+3i a forma polar:
z = 4+3i = 536.9º
- La raíz cuadrada de z,
tendrá de módulo la raíz cuadrada del módulo
de z, y de argumento, el de z
dividido por 2.
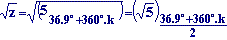
- Las dos soluciones de
esta raíz cuadrada
son:
Si k=0 --> z1=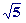 18.4º 18.4º
Si k=1 --> z2=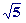 198.4º 198.4º
Si le sigues dando valores a k (k=2, 3, 4, ...) verás
que las soluciones que salen coinciden con las ya mencionadas, después
de haber dado 1, 2, 3, ... vueltas a la circunferencia. Todas
estas operaciones que hemos hecho las puedes ver en la escena, y ver
cómo quedan los vectores, tanto de z como de z1
y z2
|
EJERCICIO 12
Calcula en tu cuaderno las dos raices cuadradas de
a)
z = 1-i b)
z = -9
c)
z = 4i
d)
z = -2+2i
Después comprueba tus resultados
en la escena.
NOTA: Después
de introducir los valores de a y b, debes darle al botón limpiar.
Pero, cuando cambias de k=0 a k=1 no es necesario, así verás las
dos soluciones a la vez.
9.2
RAÍZ CÚBICA
Calcularemos 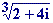 fijándonos al mismo tiempo en la siguiente escena:
fijándonos al mismo tiempo en la siguiente escena:
|
|
- Primero, pasamos z=2+4i
a forma polar:
z = 2+4i = 4.563.4º
- La raíz cúbica de z, tendrá
de módulo la raíz cúbica del módulo de
z y de argumento, el de z dividido por 3.
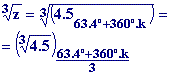
- Las tres soluciones
de esta raíz cúbica son:
| Si k=0 -> z1=1.621.1º |
Si k=1 -> z2=1.6141.1º |
Si k=2 -> z3=1.6261.1º |
Si le sigues dando valores a
k (k=2, 3, 4, ...) verás que las soluciones que salen coinciden
con las ya mencionadas, después de haber dado 1, 2, 3, ... vueltas
a la circunferencia. Todas estas operaciones que
hemos hecho las puedes ver en la escena, y ver cómo quedan los
vectores, tanto de z como de z1 , z2
y z3
|
EJERCICIO 13
Calcula en tu cuaderno las tres raices cúbicas
de
a)
z = -i b)
z = -8 c)
z = 6 d)
z = -2+3i
Después comprueba tus resultados
en la escena.
Nota: Después de
introducir los valores de a y b, debes darle al botón limpiar.
Pero cuando cambias de k=0 a k=1 y k =2 no es necesario, así verás
las tres soluciones a la vez.
EJERCICIO 14
Comprueba en la escena anterior las tres raices cúbicas
del complejo z = 890º que habíamos estudiado
al principio de esta lección.
Ten en cuenta que en esta escena tienes que introducir
el complejo en forma binómica.
9.3
RAÍZ n-ÉSIMA
En esta escena podrás calcular las
n raíces n-ésimas
(o sea, de índice n) de cualquier complejo
z, dado en forma polar.
|
|
EJERCICIO
15
1. Calcula
en tu cuaderno:
a) 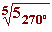 b)
b) 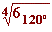 c)
c) 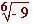 d)
d) 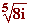
Comprueba tus resultados en esta escena,
y debes darlos en forma polar y en forma binómica.
Nota: En esta escena
hay que introducir los complejos en forma polar; por tanto, si nos lo
dieran en forma binómica, habría que hacer previamente
el cambio.
Cada vez que introduzcas un nuevo complejo hay
que limpiar la escena.
EJERCICIO 16
Comprueba en la escena anterior las cuatro raices
cuartas del complejo z= 1240º que habíamos estudiado
en el segundo ejemplo de esta lección.
Ten en cuenta que en esta escena tienes que introducir
el complejo en forma binómica.
|
;